
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия равновесия тела. Аксиомы статики. Связи и их реакции. Основные формы уравнений равновесия для плоской системы сил.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Статика (от греч. statike — учение о весе, о равновесии) - раздел механики, посвященный изучению условий равновесия материальных тел под действием сил. Понятия статики вошли в науку как результат многовековой практической деятельности человека. Они подтверждены опытами и наблюдениями над явлениями природы. Тело можно рассматривать как материальную точку, т. е. его можно представить геометрической точкой, в которой сосредоточена вся масса тела, в том случае, когда размеры тела не имеют значения в рассматриваемой задаче. Например, при изучении движения планет и спутников их считают материальными точками, так как размеры планет и спутников пренебрежимо малы по сравнению с размерами их орбит. С другой стороны, изучая движение планеты (например, Земли) вокруг оси, ее уже нельзя считать материальной точкой. Тело можно считать материальной точкой во всех случаях, когда все его точки совершают тождественные движения. Системой называется совокупность материальных точек, движения и положения которых взаимозависимы. Из приведенного определения следует, что любое физическое тело можно рассматривать как систему материальных точек. Рассматривая равновесие тел, их считают абсолютно твердыми (или абсолютно жесткими), т. е. предполагают, что никакие внешние воздействия не вызывают изменения их размеров и формы и что расстояние между любыми двумя точками тела всегда остается неизменным. В действительности все тела под влиянием силовых воздействий со стороны других тел деформируются и изменяют свои размеры или форму. Но материалы, форму и размеры элементов конструкций подбирают с таким расчетом, чтобы их деформации были минимальными, поэтому такими деформациями пренебрегают и рассматривают элементы конструкций как абсолютно твердые тела. Абсолютно твердые тела могут вступать во взаимодействие, в результате которого изменяется характер их движения. Сила является мерой этого взаимодействия. Например, взаимодействие планет и Солнца определяется силами тяготения. Действие силы на тело определяется тремя факторами: численным значением, направлением и точкой приложения, т. е. сила является векторной величиной. Статика основана на аксиомах: 1. Первая аксиома определяет уравновешенную систему сил. Система сил, приложенная к материальной точке, является уравновешенной, если под ее воздействием точка находится в состоянии относительного покоя или движется равномерно и прямолинейно.
2. Вторая аксиома устанавливает условие равновесия двух сил. Две равные по модулю или численному значению силы F1=F2, приложенные к абсолютно твердому телу и направленные по одной прямой в противоположные стороны, взаимно уравновешиваются. 3. Третья аксиома служит основой для преобразования сил. Не нарушая механического состояния абсолютно твердого тела, к нему можно приложить или отбросить от него уравновешенную систему сил. 4. Четвертая аксиома определяет правило сложения двух сил. Равнодействующая двух сил, приложенных к одной точке, приложена в этой точке и является диагональю параллелограмма, построенного на данных силах. 5. Пятая аксиома устанавливает, что в природе не может быть одностороннего действия силы. При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие. Рассматриваемые в механике тела могут быть свободными и несвободными. Свободным называют тело, которое не испытывает никаких препятствий для перемещения в пространстве в любом направлении. Если же тело связано с другими телами, которые ограничивают его движение в одном или нескольких направлениях, то оно является несвободным. Тела, которые ограничивают движение рассматриваемого тела, называют связями. При взаимодействии между телом и его связями возникают силы, противодействующие возможным движениям тела. Эти силы действуют на тело со стороны связей и называются реакциями связей. Реакция связи всегда противоположна тому направлению, по которому связь препятствует движению тела. Существование реакций обосновывается аксиомой о действии и противодействии. Для определения реакций связей используют принцип освобождения от связей. Не изменяя равновесия тела, каждую связь можно отбросить, заменив ее реакцией. Определение реакций связей является одной из наиболее важных задач статики. 1. Связь в виде гладкой (т. е. без трения) плоскости или поверхности. 2. Связь в виде контакта цилиндрической или шаровой поверхности с плоскостью.
3. Cвязь в виде шероховатой плоскости. 4. Гибкая связь 5. Связь в виде жесткого прямого стержня с шарнирным закреплением концов. 6. Связь, осуществляемая ребром двугранного угла или точечной опорой. В системе сходящихся сил равнодействующая может быть найдена через проекции составляющих. Рассмотрим ее определение на примере системы F1,F2,F3,F4 сил, изображенной на рисунке стр. 18. Равнодействующая этих сходящихся сил построена на рисунке:
Проектируя все силы на оси Ох и Оу и испвльзуя теорему о проекции векторной суммы, получает:
Численное значение равнодействующей силы Получаем:
Уравнения плоской системы сходящихся сил Сходящаяся система сил находится в равновесии в случае замкнутости силового многоугольника. Равнодействующая при этом равна нулю (
Оба слагаемых, стоящих под знаком корня, во всех случаях положительны как величины, возведенные в квадрат. Поэтому
Рассматриваемая система сходящихся сил находится в равновесии, когда алгебраические суммы проекций ее слагаемых на каждую из двух координатных осей равны нулю. Эти зависимости называют уравнениями равновесия плоской системы сходящихся сил и используют при аналитическом решении задач. Содержание дисциплины «Машиноведение»
|
||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.117.95 (0.01 с.) |



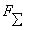 через ее проекции определяется по формуле
через ее проекции определяется по формуле 







