
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для тонкого растяжимого стержня закон Гука имеет вид:
Определим внутренние силовые факторы в поперечных сечениях стержня, растянутого двумя равными силами F. Рассечём стержень произвольным поперечным сечением и, рассматривая равновесие нижней части, найдем величину продольной силы:
В случае растяжения продольную силу N будем считать положительной, при сжатии — отрицательной. Изменение продольной силы по длине стержня удобно представить в виде диаграммы, называемой эпюрой продольных сил.
3.Общая характеристика деформации среза (сдвига) и смятия, условия прочности при срезе (сдвиге) и смятии. Закон Гука при чистом сдвиге. Срезом или сдвигом называется деформация, возникающая под действием двух близко расположенных противоположно направленных равных сил. При этом возникают касательные напряжения. Примером элемента металлических конструкций, работающего на срез, может служить заклепка (рис. 75, а). При некоторой величине действующих сил F стержень заклепки может быть срезан по сечению аа. Силы F (рис. 75, б) передаются путем давления стенок отверстия на стержень заклепки. Сдвиг — вид продольной деформации бруса, возникающий в том случае, если сила прикладывается касательно его поверхности (при этом нижняя часть бруска закреплена неподвижно). Относительная деформация сдвига определяется по формуле:
где Δx — абсолютный сдвиг параллельных слоёв тела относительно друг друга; l — расстояние между слоями (для малых углов
Смятием называется местная деформация сжатия по площадкам передачи давления. Возникающие нормальные напряжения смятия являются местными; величина их быстро убывает при удалении от площадки соприкосновения элементов.
При возникновении касательных напряжений элемент перекашивается. Если считать грань ad закрепленной, то грань bc сдвинется в положение b1c1. Прямые углы между гранями изменяются на величину Касательные напряжения
Входящая в эту формулу величина G называется модулем сдвига. Эта величина характеризует жесткость материала при деформации сдвига. Так как Между модулем упругости Е и модулем сдвига G существует зависимость, которую приводим без вывода:
где
|
|||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.36.89 (0.007 с.) |

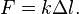

 ,
, )
) Деформация среза возникает также в шпоночном соединении, схематично изображенном на рис.. Вращающий момент М от шкива передается на вал радиуса г с помощью сил F = M/r. Эти силы вызывают срез или сдвиг шпонки по ее среднему сечению. Частный случай среза — скалывание волокнистых материалов, в частности древесины, по плоскостям, параллельным волокнам. При большом давлении может произойти значительное смятие стенок отверстия или стержня заклепки по поверхности их соприкосновения. В шпоночном соединении смятие может произойти по площади контакта вала или шкива со шпонкой.
Деформация среза возникает также в шпоночном соединении, схематично изображенном на рис.. Вращающий момент М от шкива передается на вал радиуса г с помощью сил F = M/r. Эти силы вызывают срез или сдвиг шпонки по ее среднему сечению. Частный случай среза — скалывание волокнистых материалов, в частности древесины, по плоскостям, параллельным волокнам. При большом давлении может произойти значительное смятие стенок отверстия или стержня заклепки по поверхности их соприкосновения. В шпоночном соединении смятие может произойти по площади контакта вала или шкива со шпонкой. . Угол
. Угол  и угол сдвига
и угол сдвига 

 — коэффициент поперечной деформации (коэффициент Пуассона).
— коэффициент поперечной деформации (коэффициент Пуассона).


