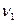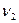Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Территориальный индекс цен равен
Похожие статьи вашей тематики
 , ,
Где
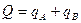 . .
2. Соотношение весов сравниваемых регионов учтено в следующем способе расчета территориального индекса цены:
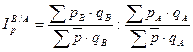 , ,
При этом
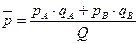 . .
3. Индекс физического объема реализации подсчитывается по формуле:
 . .
4. Расчет индексов 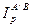 и и 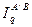 производится аналогично. производится аналогично.
Составляем расчетную таблицу:
| Товар
| А
| В
| Расчетные графы
| 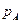
| 
| 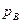
| 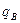
| 
| 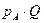
| 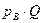
| |
|
| 175,5
| 10,7
|
| 375,5
|
| 4017,85
| |
|
| 38,45
| 14,2
| 40,04
| 78,49
| 1098,86
| 1114,558
| |
| 8,4
| 118,22
| 8,3
| 150,25
| 268,47
| 2255,148
| 2228,301
| 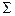
| -
| -
| -
| -
| 722,46
| 7109,008
| 7360,709
|
| Товар
| Расчетные графы
| 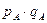
| 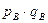
| 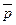
| 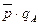
| 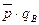
| |
|
|
| 10,3728
| 1820,4328
| 2074,5672
| |
| 538,3
| 568,568
| 14,1020
| 542,2229
| 564,6451
| |
| 993,048
| 1247,075
| 8,3440
| 986,4318
| 1253,6912
| 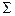
| 3286,348
| 3955,643
| -
| 3349,0874
| 3892,9036
|
Получаем:
 или 103,54%, или 103,54%,
что говорит о том, что цены в регионе В на 3,54% выше, чем в регионе А.
Территориальный индекс цен, найденный вторым способом, равен
 или 103,55%. или 103,55%.
Территориальный индекс объема
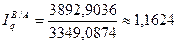 или 116,24%. или 116,24%.
Итак, объем реализации в регионе В в среднем на 16,24% выше, чем в регионе А.

Для заметок
V. ПРИЛОЖЕНИЯ
1. Экзаменационные вопросы по курсу «Статистика»
|
| Предмет, методы и задачи статистики.
| |
| Закон больших чисел как теоретическая основа выборочного метода.
| |
| Выборка. Понятие выборки. Виды выборок. Вариационное распределение.
| |
| Группированный статистический ряд.
| |
| Графическое представление выборки. Полигон частот.
| |
| Графическое представление выборки. Гистограмма частот.
| |
| Графическое представление выборки. Кумулятивная кривая.
| |
| Расчет вероятности попадания значения признака в заданный интервал.
| |
| Средние величины.
| |
| Квартили, децили, перцентили.
| |
| Мода и медиана.
| |
| Показатели вариации значений признака.
| |
| Метод моментов.
| |
| Доверительная вероятность. Доверительный интервал.
| |
| Расчет требуемого объема выборочной совокупности.
| |
| Статистические гипотезы. Виды гипотез. Критерии согласия.
| |
| Критерий согласия Пирсона.
| |
| Проверка гипотезы о нормальном распределении генеральной совокупности.
| |
| Функциональная и корреляционная зависимости.
| |
| Задачи теории корреляции.
| |
| Эмпирические линии регрессии.
| |
| Метод наименьших квадратов.
| |
| Коэффициент линейной корреляции и его свойства.
| |
| Корреляционное отношение и его свойства.
| |
| Линейная корреляционная зависимость. Нахождение параметров. прямой линии регрессии с помощью системы нормальных уравнений.
| |
| Линейная корреляционная зависимость. Упрощенный способ нахождения параметров прямой линии регрессии (с помощью ρ).
| |
| Нелинейная корреляционная зависимость. Основные виды и расчет параметров зависимостей.
| |
| Проверка статистической значимости регрессионной модели
| |
| Проверка точности регрессионной модели
| |
| Выбор регрессионной модели
| |
| Множественная регрессия. Понятие. Задачи. Основные виды.
| |
| Множественный коэффициент корреляции. Общее определение Статистический смысл. Частный случай для двух факторных признаков.
| |
| Линейная многофакторная регрессия. Способы расчета параметров модели.
| |
| Коэффициент эластичности.
| |
| Дельта коэффициент.
| |
| Общий индекс детерминации.
| |
| Проверка статистической значимости и точности многофакторной модели.
| |
| Задача понижения числа факторов в многофакторной модели и способы ее решения.
| |
| Ряды динамики. Основные определения.
| |
| Сравнение уровней ряда динамики.
| |
| Средние значения числовых характеристик ряда динамики.
| |
| Выявление основных тенденций ряда динамики. Функции тренда.
| |
| Индексы сезонности.
| |
| Математическая модель ряда динамики.
| |
| Уравнение Фурье
| |
| Прогнозирование уровней ряда динамики.
| |
| Индивидуальные индексы.
| |
| Сводные индексы.
| |
| Расчет сводных индексов по формулам средних.
| |
| Цепные индексы.
| |
| Индексы переменного, постоянного состава и структурных сдвигов.
| |
| Территориальные индексы.
| |
| Показатели численности населения.
| |
| Показатели миграции.
| |
| Показатели воспроизводства населения.
| |
| Демографические прогнозы.
| |
| Характеристики занятости.
| |
| Понятие и виды безработицы.
| |
| Показатели национального богатства.
| |
| Статистика основного капитала.
| |
| Статистическое исследование оборотного капитала.
| |
| Система показателей результатов экономической деятельности.
| |
| Расчет валового выпуска продуктов и услуг и связанных с ним затрат.
| |
| Методы расчета ВВП и его оценки.
| |
| Статистика эффективности экономической деятельности.
| |
| Система показателей жизненного уровня населения.
| |
| Статистика доходов населения.
| |
| Статистика расходов и сбережений населения.
| |
| Статистические показатели условий жизни, труда и отдыха.
| |
| Статистика предприятия.
| |
| Статистика производства и реализации продукции.
| |
| Статистика качества продукции и качества работы.
| |
| Статистика численности работников и использования рабочего времени.
| |
| Статистка производительности труда.
| |
| Статистика оплата труда.
| |
| Статистика основных фондов.
| |
| Статистика оборотных средств.
| |
| Статистика издержек производства и обращения.
| |
| Статистика финансовых результатов.
| |
| Статистика домашних хозяйств.
|
Таблицы
Таблица 1. Значения функции 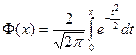
| Це лые
и десятые доли
X
| сотые доли х
|
|
|
|
|
|
|
|
|
|
| | 0,0
| 0,0000
| 0,0080
| 0,0160
| 0,0239
| 0,0319
| 0,0399
| 0,0478
| 0,0558
| 0,0638
| 0,0717
| | 0,1
| 0,0797
| 0,0876
| 0,0955
| 0,1034
| 0,1113
| 0,1192
| 0,1271
| 0,1350
| 0,1428
| 0,1507
| | 0,2
| 0,1585
| 0,1683
| 0,1174
| 0,1819
| 0,1897
| 0,1974
| 0,2025
| 0,2128
| 0,2205
| 0,2282
| | 0,3
| 0,2358
| 0,2434
| 0,2510
| 0,2586
| 0,2661
| 0,2737
| 0,2812
| 0,2886
| 0,2960
| 0,3035
| | 0.4
| 0,3108
| 0,3182
| 0,3255
| 0,3328
| 0,3401
| 0,3473
| 0,3545
| 0,3616
| 0,3668
| 0,3579
| | 0,5
| 0,3829
| 0,3889
| 0,3969
| 0,4039
| 0,4108
| 0,4177
| 0,4245
| 0,4313
| 0,4338
| 0,4448
| | 0,6
| 0,4515
| 0,4581
| 0,4647
| 0,4713
| 0,4778
| 0,4843
| 0,4907
| 0,4971
| 0,5035
| 0,5098
| | 0,7
| 0,5161
| 0,5223
| 0,5285
| 0,5346
| 0,5407
| 0,5467
| 0,5527
| 0,5587
| 0,5646
| 0,5705
| | 0,8
| 0,5763
| 0,5821
| 0,5878
| 0,5935
| 0,5991
| 0,6047
| 0,6102
| 0,6157
| 0,6211
| 0,6265
| | 0,9
| 0,6319
| 0,6372
|
| 0,6476
| 0,6528
| 0,6579
| 0,6629
| 0,6679
| 0,6729
| 0,6778
| | 1,0
| 0,6827
| 0,6875
| 0,6923
| 0,6970
| 0,7017
| 0,7063
| 0,7109
| 0,7154
| 0,7199
| 0,7243
| | 1,1
| 0,7287
| 0,7330
| 0,7373
| 0,7415
| 0,7457
| 0,7499
| 0,7540
| 0,7580
| 0,7620
| 0,7660
| | 1,2
| 0,7699
| 0,7737
| 0,7775
| 0,7813
| 0,7850
| 0,7887
| 0,7923
| 0,7959
| 0,7994
| 0,8029
| | 1,3
| 0,8064
| 0,8098
| 0,8132
| 0,8165
| 0,8198
| 0,8230
| 0,8262
| 0,8293
| 0,8324
| 0,8355
| | 1,4
| 0,8385
| 0,8415
| 0,8444
| 0,8473
| 0,8501
| 0,8529
| 0,8557
| 0,8584
| 0,8611
| 0,8638
| | 1,5
| 0,8664
| 0,8690
| 0,8715
| 0,8740
| 0,8764
| 0,8789
| 0,8812
| 0,8836
| 0,8859
| 0,8882
| | 1,6
| 0,8904
| 0,8926
| 0,8948
| 0,8969
| 0,8990
| 0,9011
| 0,9031
| 0,9051
| 0,9070
| 0,9090
| | 1,7
| 0,9109
| 0,9127
| 0,9146
| 0,9164
| 0,9181
| 0,9199
| 0,9216
| 0,9233
| 0,9249
| 0,9265
| | 1,8
| 0,9281
| 0,9297
| 0,9312
| 0,9327
| 0,9342
| 0,9357
| 0,9371
| 0,9385
| 0,9399
| 0,9412
| | 1,9
| 0,9426
| 0,9439
| 0,9451
| 0,9464
| 0,9476
| 0,9488
| 0,9500
| 0,9512
| 0,9523
| 0,9534
| | 2,0
| 0,9545
| 0,9556
| 0,9566
| 0,9576
| 0,9586
| 0,9596
| 0,9606
| 0,9616
| 0,9625
| 0,9634
| | 2,1
| 0,9643
| 0,9651
| 0,9660
| 0,9668
| 0,9676
| 0,9684
| 0,9692
| 0,9700
| 0,9707
| 0,9715
| | 2,2
| 0,9722
| 0,9729
| 0,9736
| 0,9743
| 0,9749
| 0,9756
| 0,9762
| 0,9768
| 0,9774
| 0,9780
| | 2,3
| 0,9786
| 0,9791
| 0,9797
| 0,9802
|
| 0,9812
| 0,9817
| 0,9822
| 0,9827
| 0,9832
| | 2,4
| 0,9836
| 0,9841
| 0,9845
| 0,9849
| 0,9853
| 0,9857
| 0,9861
| 0,9865
| 0,9869
| 0,9872
| | 2,5
| 0,9876
| 0,9879
| 0,9883
| 0,9886
| 0,9889
| 0,9892
| 0,9895
| 0,9898
| 0,9901
| 0,9904
| | 2,6
| 0,9907
| 0,9910
| 0,9912
| 0,9915
| 0,9917
| 0,9920
| 0,9922
| 0,9924
| 0,9926
| 0,9928
| | 2,7
| 0,9931
| 0,9933
| 0,9935
| 0,9937
| 0,9939
| 0,9940
| 0,9942
| 0,9944
| 0,9946
| 0,9947
| | 2,8
| 0,9949
| 0,9951
| 0,9952
| 0,9953
| 0,9955
| 0,9956
| 0,9958
| 0,9959
| 0,9960
| 0,9961
| | 2,9
| 0,9963
| 0,9964
| 0,9965
| 0,9966
| 0,9967
| 0,9968
| 0,9969
| 0,9970
| 0,9971
| 0,9972
| | 3,0
| 0,9973
| 0,9974
| 0,9975
| 0,9976
| 0,9976
| 0,9977
| 0,9978
| 0,9979
| 0,9979
| 0,9980
|
Таблица 1. Продолжение
| Це лые
и десятые доли
X
|
| | сотые доли х
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| | 3,1
| 0,9981
| 0,9981
| 0,9982
| 0,9983
| 0,9983
| 0,9984
| 0,9984
| 0,9985
| 0,9985
| 0,9986
| | 3,2
| 0,9986
| 0,9987
| 0,9987
| 0,9988
| 0,9988
| 0,9989
| 0,9989
| 0,9989
| 0,9990
| 0,9990
| | 3,3
| 0,9990
| 0,9991
| 0,9991
| 0,9991
| 0,9992
| 0,9992
| 0,9992
| 0,9992
| 0,9993
| 0,9993
| | 3,4
| 0,9993
| 0,9994
| 0,9994
| 0,9994
| 0,9994
| 0,9994
| 0,9995
| 0,9995
| 0,9995
| 0,9995
| | 3,5
| 0,9995
| 0,9996
| 0,9996
| 0,9996
| 0,9996
| 0,9996
| 0,9996
| 0,9996
| 0,9997
| 0,9997
| | 3,6
| 0,9997
| 0,9997
| 0,9997
| 0,9997
| 0,9997
| 0,9997
| 0,9997
| 0,9998
| 0,9998
| 0,9998
| | 3,7
| 0,9998
| 0,9998
| 0,9998
| 0,9998
| 0,9998
| 0,9998
| 0,9998
| 0,9998
| 0,9998
| 0,9998
| | 3,8
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| | 3,9
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| | 4,0
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
| 0,9999
|
Таблица 2. Некоторые значения 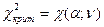 критерия Пирсона критерия Пирсона
|
|
| ν
|
|
|
|
|
|
|
|
|
|
| | α
|
|
| |
| 0,05
|
| 3,84
| 5,99
| 7,82
| 9,49
| 11,1
| 12,6
| 14,1
| 15,5
| 16,9
| 18,3
| |
| 0,01
|
| 6,64
| 9,21
| 11,3
| 13,3
| 15,1
| 16,8
| 18,5
| 20,1
| 21,7
| 23,2
|
Таблица 3. Некоторые значения 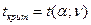 критерия Стьюдента критерия Стьюдента
| ν
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| | α
|
|
|
|
|
|
|
|
|
|
| | 0,05
| 12,70
| 4,30
| 3,18
| 2,78
| 2,57
| 2,45
| 2,36
| 2,31
| 2,26
| 2,23
| | 0,01
| 63,70
| 9,92
| 5,84
| 4,60
| 4,03
| 3,71
| 3,50
| 3,36
| 3,25
| 3,17
| | ν
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| | α
|
|
|
|
|
|
|
|
|
|
| | 0,05
| 2,20
| 2,18
| 2,16
| 2,14
| 2,13
| 2,12
| 2,11
| 2,10
| 2,09
| 2,09
| | 0,01
| 3,11
| 3,05
| 3,01
| 2,98
| 2,95
| 2,92
| 2,90
| 2,88
| 2,86
| 2,85
| | ν
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| | α
|
|
|
|
|
|
|
|
|
|
| | 0,05
| 2,08
| 2,07
| 2,07
| 2,06
| 2,06
| 2,06
| 2,05
| 2,05
| 2,05
| 2,04
| | 0,01
| 2,83
| 2,82
| 2,81
| 2,80
| 2,79
| 2,78
| 2.77
| 2,76
| 2,76
| 2,75
| | ν
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
| ∞
|
|
|
|
|
| | α
|
|
|
|
|
|
|
|
|
|
| | 0,05
| 2,02
| 2,00
| 1,99
| 1,98
| 1,96
|
|
|
|
|
| | 0,01
| 2,70
| 2,66
| 2,64
| 2,62
| 2,58
|
|
|
|
|
|
Таблица 4. Некоторые значения Fкрит = 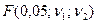 критерия Фишера критерия Фишера
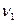
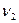
|
|
|
|
|
|
|
|
|
| ∞
| |
| 161,40
| 199,50
| 215,70
| 224,60
| 230,20
| 234,00
| 238,90
| 243,90
| 249,00
| 25.'UO
| |
| 18,51
| 19,00
| 19,16
| 19,25
| 19,30
| 19,33
| 19,37
| 19,41
| 19,45
| 19,50
| |
| 10,13
| 9,55
| 9,28
| 9,12
| 9,01
| 8,94
| 8,84
| 8,74
| 8,64
| 8,53
| |
| 7,71
| 6.9!
| 6,59
| 6,39
| 6,26
| 6,16
| 6,04
| 5,91
| 5,77
| 5,63
| |
| 6,61
| 5,79
| 5,41
| 5,19
| 5,05
| 4,95
| 4,82
| 4,68
| 4,53
| 4,30
| |
| 5,99
| 5,14
| 4,76
| 4,53
| 4,39
| 4,28
| 4,15
| 4,00
| 3,84
| 3,67
| |
| 5,59
| 4.74
| 4,35
| 4,12
| 3,97
| 3,87
| 3,73
| 3,57
| 3,41
| 3,23
| |
| 5,32
| 4,46
| 4,07
| 3,84
| 3,69
| 3,58
| 3,44
| 3,28
| 3,12
| 2,99
| |
| 5,12
| 4,20
| 3,86
| 3,63
| 3,48
| 3,37
| 3,23
| 3,07
| 2,90
| 2,71
| |
| 4,96
| 4,10
| 3,71
| 3,48
| 3,33
| 3,22
| 3,07
| 2,91
| 2,74
| 2,54
| |
| 4,84
| 3,98
| 3,59
| 3,36
| 3,20
| 3,09
| 2,95
| 2,79
| 2,61
| 2,40
| |
| 4,75
| 3,88
| 3,49
| 3,26
| 3,11
| 3,00
| 2,85
| 2,69
| 2,50
| 2,30
| |
| 4.67
| 3,80
| 3,41
| 3,18
| 3,02
| 2,92
| 2,77
| 2,60
| 2,42
| 2,21
| |
| 4,60
| 3,7 I
| 3,34
| 3,11
| 2,96
| 2,85
| 2,70
| 2,53
| 2,35
| 2,13
| |
| 4,45
| 3,68
| 3,29
| 3,06
| 2,90
| 2,79
| 2,64
| 2,48
| 2,29
| 2,07
| |
| 4,41
| 3,63
| 3,24
| 3,01
| 2,83
| 2,74
| 2,59
| 2,42
| 2,24
| 2,01
| |
| 4,45
| 3,59
| 3,20
| 2,96
| 2,81
| 2,70
| 2,55
| 2,38
| 2,19
| 1,96
| |
| 4,41
| 3,5й
| 3,16
| 2,93
| 2,77
| 2,66
| 2,51
| 2,34
| 2,15
| 1,92
| |
| 4,38
| 3,52
| 3,13
| 2,90
| 2,74
| 2,63
| 2,48
| 2,31
| 2,11
| 1,88
| |
| 4,35
| 3,49
| 3,10
| 2,87
| 2,71
| 2,60
| 2,45
| 2,28
| 2,08
| 1,84
| |
| 4,32
| 3,47
| 3,07
| 2,84
| 2,68
| 2,57
| 2,42
| 2,25
| 2,05
| 1,82
| |
| 4,30
| 3,44
| 3,05
| 2,82
| 2,66
| 2,55
| 2,40
| 2,23
| 2,03
| 1,78
| |
| 4,28
| 3,42
| 3,03
| 2,80
| 2,64
| 2,53
| 2,38
| 2,20
| 2,00
| 1,76
| |
| 4,26
| 3,40
| 3,01
| 2,78
| 2,62
| 2,51
| 2,36
| 2,18
| 1,98
| 1,73
| |
| 4,24
| 3,38
| 2,99
| 2,76
| 2,00
| 2,49
| 2,34
| 2,16
| 1,96
| 1,71
| |
| 4,22
| 3,37
| 2,98
| 2,74
| 2,59
| 2,47
| 2,32
| 2,15
| 1,95
| 1,69
| |
| 4,21
| 3,35
| 2,96
| 2,73
| 2,57
| 2,46
| 2,30
| 2,13
| 1,93
| 1,67
| |
| 4,19
| 3,34
| 2,95
| 2,71
| 2,56
| 2,44
| 2,29
| 2,12
| 1,91
| 1,65
| |
| 4,18
| 3,33
| 2,93
| 2,70
| 2,54
| 2,43
| 2,28
| 2,10
| 1,90
| 1,64
| |
| 4,17
| 3,32
| 2,92
| 2,69
| 2,53
| 2,42
| 2,27
| 2,09
| 1,89
| 1,62
| |
| 4,00
| 3,15
| 2,70
| 2,52
| 2,37
| 2,25
| 2,10
| 1,92
| 1,70
| 1,39
| | ∞
| 3,84
| 2,99
| 2,00
| 2,37
| 2,21
| 2,09
| 1,94
| 1,75
| 1,52
| 1,03
|
Литература
1. Статистика: Учебник / Под ред. В. С. Мхитаряна. - М.: Экономистъ, 2005. – 671 с.
2. Экономическая статистика: Учебник / Под ред. Ю. Н. Иванова. – М.: Инфра – М, 1998. – 480 с.
3. Практикум по теории статистики: Учебное пособие / Под ред. Р. А. Шмойловой. – М.: Финансы и статистика, 1999 – 416 с.
4. И. Г. Венецкий, В. И. Венецкая. Основные математико – статистические понятия и формулы в экономическом анализе. М.: Статистика, 1979. – 447 с.
5. В. Е. Крылов. Теория вероятностей и математическая статистика (тексты лекций). Владимир.: ВИБ, 2004 – 189 с.
6. В. Е. Крылов. Статистическая обработка результатов наблюдений (методические указания к решению задач по математической статистике). Владимир.: ВИБ, 2004 – 22 с.
7. В. Е. Крылов. Корреляционно – регрессионный анализ (методические указания к решению задач по математической статистике). Владимир.: ВИБ, 2004 – 189 с.
|



 ,
,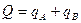 .
.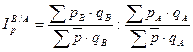 ,
,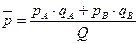 .
. .
.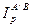 и
и 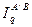 производится аналогично.
производится аналогично.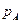

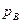
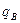

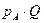
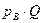
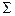
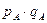
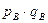
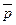
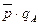
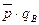
 или 103,54%,
или 103,54%, или 103,55%.
или 103,55%.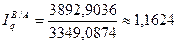 или 116,24%.
или 116,24%.
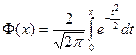
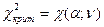 критерия Пирсона
критерия Пирсона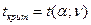 критерия Стьюдента
критерия Стьюдента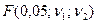 критерия Фишера
критерия Фишера