
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. «Проверка статистических гипотез»Содержание книги
Поиск на нашем сайте Задача 8. С вероятностью 0,95 проверить гипотезу о том, что генеральная совокупность, которой принадлежит выборка из задачи 1, распределена по нормальному (Гауссову) закону распределения случайной величины. Гипотеза о нормальном распределении генеральной совокупности, которой принадлежит исследуемая выборка, с доверительной вероятностью γ проверяется с помощью Сравниваем полигон частот выборочной совокупности с графиком функции плотности
идеального нормального распределения (рисунок 7). Если они похожи, то переходим к следующему пункту алгоритма. В противном случае утверждаем, что с помощью имеющейся совокупности проверить гипотезу невозможно. Сравниваем кумулятивную кривую с графиком интегральной функции
идеального нормального распределения (рисунок 8). Выводы аналогичны пункту 1 алгоритма.
Рис. 7
 Рис. 8 Рис. 8
По знаку асимметрии и эксцесса устанавливаем вид распределения (см. таблицу 9). Таблица 9
4. По величине асимметрии и эксцесса устанавливаем тип распределения: а) если as = es =0 – идеальное нормальное распределение; б) если | as |<0,1,| es |<1 - нормальное распределение; в) если | as |<0,5, | es |<0,5 – распределение, близкое к нормальному; г) если | as |<1, | es |<1 – распределение нормального типа. 5. Производим частот теоретических частот
где 6. Чтобы убедиться, что теоретические частоты адекватно описывают эмпирические данные, на одном чертеже строим кривую нормального распределения 7. Находим наблюдаемое значение критерия Пирсона по формуле:
8. С вероятностью γ выдвигаем гипотезу о нормальном распределении генеральной совокупности, которой принадлежит выборка. Для этого по таблице 2 Приложения критических значений критерия Пирсона определяем критическое значение
k – число интервалов группировки. Выводы производятся на основании следующего утверждения: если
То гипотеза о нормальном распределении генеральной совокупности, которой принадлежит исследуемая выборка, принимается с указанной вероятностью. В противном случае гипотеза отвергается с той же вероятностью. Сравнивая рисунки 4 и 7, делаем вывод об их похожести. Сравнивая рисунки 6 и 8, делаем вывод об их похожести. Согласно задаче 4 (или 5)
следовательно (см. таблицу 9) рассматриваемое распределение является левосторонним островершинным. Так как одновременно
то наше распределение имеет нормальный тип. Используем результаты решения задач 4 и 5: n = 100, Тогда, теоретические частоты рассчитываются так:
Находим их в расчетной таблице:
На одном графике (рисунок 9) строим кривую теоретических частот (сплошная линия) и полигон частот (пунктирная линия).
Рис. 9 Сравнение графиков наглядно показывает, что найденные результаты расчетов адекватно описывают эмпирические данные. Находим наблюдаемое значение критерия Пирсона. Расчеты производим в таблице:
Итак,
Доверительная вероятность γ = 0,95, отсюда уровень значимости α = 1-0,95 = 0,05. Число интервалов группировки k = 8, тогда ν = 8 -3 = 5. Отсюда, критическое значение согласно таблице 2 Приложения равно
Так как 11,0499<11,1, то гипотеза о том, что генеральная совокупность, которой принадлежит выборка из задачи 1, распределена нормально, принимается с вероятностью 0,95.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 - критерия согласия Пирсона (критерия хи - квадрат). Приведем алгоритм проверки гипотезы с помощью этого критерия.
- критерия согласия Пирсона (критерия хи - квадрат). Приведем алгоритм проверки гипотезы с помощью этого критерия.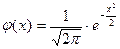








 каждого из интервалов группировки (α;β), рассчитанных в предположении, что выборочная совокупность распределена по нормальному закону распределения:
каждого из интервалов группировки (α;β), рассчитанных в предположении, что выборочная совокупность распределена по нормальному закону распределения: ,
, ,
,  ,
, - функция Лапласа, значения которой приведены в таблице 1 Приложения. Заметим, что функция Лапласа – нечетная, то есть
- функция Лапласа, значения которой приведены в таблице 1 Приложения. Заметим, что функция Лапласа – нечетная, то есть  .
. и полигон частот.
и полигон частот. .
.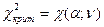 , α = 1- γ, ν = k -3,
, α = 1- γ, ν = k -3, ,
, ,
,  ,
, ,
,  ,
, ,
,  .
. ,
, ,
, 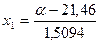 .
.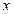




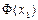
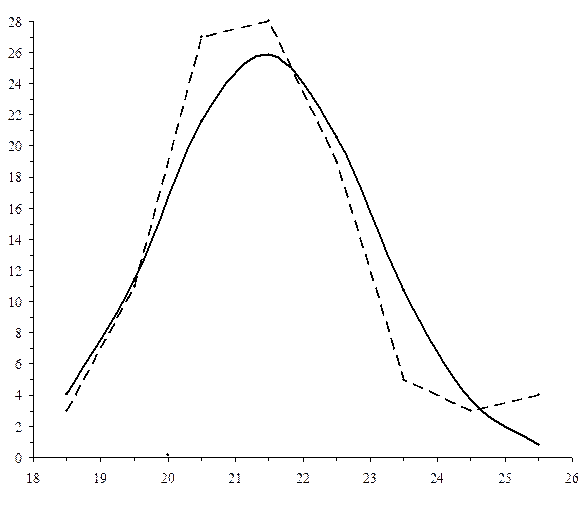




 .
.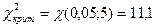 .
.


