
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Среднее значение (средняя арифметическая)Содержание книги
Поиск на нашем сайте
Среднее линейное отклонение
Дисперсия, рассчитанная по определению
Дисперсия, рассчитанная по формуле разностей
Где
Среднее квадратическое отклонение
Коэффициент вариации
Асимметрия
Эксцесс
Среднее значение, среднее линейное отклонение и среднее квадратическое отклонение являются именованными величинами. Дисперсия, асимметрия и эксцесс – неименованные величины. Если коэффициент вариации меньше 33%, то выборочная совокупность явялется плотной, однородной и по ней можно делать выводы, осуществлять прогнозы, выдвигать гипотезы. Расчеты удобно производить в следующей таблице:
Получаем:
Задача 5. Для выборки из задачи 1 методом моментов найти среднее значение дисперсию, асимметрию и эксцесс. 1. Находим шаг варьирования 2. Величина ложного нуля 3. Для каждого значения х определяем условные варианты
4. Вычисляем условные моменты:
5. Искомые значения рассчитываются по формулам:
Из группированного статистического ряда (см задачу 1) заключаем, что
Так как максимальной частоте ряда 28 соответствует значение случайной величины 21,5 (см. группированный статистический ряд, задача 1), то
Отсюда, условный вариант
Нахождение условных моментов удобно производить в таблице:
Тогда, условные варианты соответственно равны:
Итак, требуемые величины соответственно равны:
Задача 6. Для выборки из задачи 1 с вероятностью γ = 0,95 определить границы интервала, в котором заключено математическое ожидание а (генеральная средняя или среднее значение генеральной совокупности) и сделать соответствующие выводы. Задачу решить в предположении а) повторного, б) бесповторного отбора из генеральной совокупности объема N = 1500. С доверительной вероятностью γ утверждается, что математическое ожидание а принадлежит интервалу:
где
причем t – постоянная величина, значение которой определяется в зависимости от γ, в частности t = 3, если γ =0,99, t = 2, если γ =0,95, t = 1, если γ =0,63, μ – средняя ошибка выборки, равная
Имеем (см. задачу 4):
Средняя ошибка выборки равна:
Если отбор повторный или бесповторный соответственно. Тогда, в зависимости от типа отбора, предельная ошибка выборки равна:
Получаем: нижняя граница доверительного интервала:
верхняя граница доверительного интервала:
Итак, с вероятностью 0,95 можно утверждать, что средний диаметр детали, изготавливаемой предприятием находится в пределах от 21,1582 до 21,7618 мм (если выборка организована методом случайного повторного отбора) и от 21,1684 до 21,7516 мм (если выборка случайная, бесповторная).
Задача 7. Для выборки из задачи 1 с вероятностью γ = 0,99 определить границы интервала, в котором заключена генеральная доля признака р – диаметр детали, находящийся в пределах от 20 до 23 мм включительно и сделать соответствующие выводы. Задачу решить в предположении бесповторного отбора из генеральной совокупности объема N = 2000. С доверительной вероятностью γ утверждается, что математическое ожидание р принадлежит интервалу:
где
причем t – постоянная величина, значение которой определяется в зависимости от γ также, как и в задаче 6,
В выборке интересующий нас диаметр детали (от 20 до 23 мм) принадлежит интервалам (см. задачу 1) (20;21), (21;22) и (22;23), частоты которых соответственно равны 27, 28 и 19. Следовательно, выборочная доля
Согласно условию задачи находим предельную ошибку доли:
Имеем: нижняя граница доверительного интервала:
верхняя граница доверительного интервала:
Итак, с вероятностью 0,99 утверждается, что среди 2000 деталей доля деталей диаметра от 20 до 23 мм находится в пределах от 0,6117 до 0,8683 (от 61,17% до 86,83%).
Для заметок
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.239.65 (0.006 с.) |

 ;
; ;
; ;
; ,
, ;
;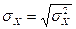 ;
; ;
; ;
; .
.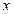









 (мм);
(мм);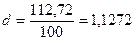 (мм);
(мм); ;
;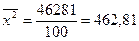 ,
, ;
; (мм);
(мм); ;
; ;
; .
. , то есть разность между любыми двумя соседними значениями случайной величины. Предполагается, что выборочной совокупности
, то есть разность между любыми двумя соседними значениями случайной величины. Предполагается, что выборочной совокупности  определяется как значение случайной величины, имеющее максимальную частоту.
определяется как значение случайной величины, имеющее максимальную частоту. .
. ;
;  ;
;  ;
;  .
. ;
; ;
; ;
; .
. .
.




 ;
;  ;
;  ;
;  .
. ;
; ;
;  ;
; .
. ,
,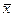 - выборочная средняя (среднее значение признака, рассчитанное по выборке), δ – предельная ошибка, равная
- выборочная средняя (среднее значение признака, рассчитанное по выборке), δ – предельная ошибка, равная ,
, - если отбор случайный – повторный,
- если отбор случайный – повторный, - если отбор случайный – бесповторный.
- если отбор случайный – бесповторный. ,
,  , n = 100, N = 1500, t = 2.
, n = 100, N = 1500, t = 2. ,
, ,
, или
или  .
. ;
; .
. ,
, - выборочная доля ( m – количество элементов выборочной совокупности, обладающих интересующим нас признаком, n – объем выборочной совокупности),
- выборочная доля ( m – количество элементов выборочной совокупности, обладающих интересующим нас признаком, n – объем выборочной совокупности),  – предельная ошибка доли, равная
– предельная ошибка доли, равная ,
, – средняя ошибка доли, равная
– средняя ошибка доли, равная - если отбор случайный – повторный,
- если отбор случайный – повторный, - если отбор случайный – бесповторный.
- если отбор случайный – бесповторный. .
. .
. ;
; .
.



