
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналогично определяется эмпирическая линия регрессии у на х – ломаная с вершинами в точках с координатамиСодержание книги
Поиск на нашем сайте
При этом
3. Коэффициент линейной корреляции r позволяет определить форму корреляционной зависимости. Он подсчитывается по формуле:
Средние квадратические отклонения группировочных признаков определяются как арифметические квадратные корни из дисперсий. Дисперсии рассчитываются по определению или по формуле разностей (см. задачу 4), а также методом моментов (см. задачу 5). Величина μ может быть найдена двумя способами: по определению
а средние арифметические
В зависимости от r имеем следующую интерпретацию связи
4. Степень тесноты корреляционной связи устанавливается с помощью корреляционного отношения η, равного
При этом
Характер связи определяется так:
Для проверки правильности произведенных вычислений удобно использовать свойство корреляционного отношения:
5. Проверить гипотезу о статистической значимости эмпирических данных, а следовательно о принципиальной возможности построения уравнения регрессионной модели можно с помощью t - критерия Стьюдента. Правило проверки гипотезы. Если наблюдаемое значение критерия больше критического,
То это с вероятностью γ (уровнем значимости α = 1- γ ) говорит о значимости коэффициента линейной корреляции, а следовательно о статистической значимости эмпирических данных. При этом
а критическое значение определяется по таблице (см. таблицу 3 Приложения):
Нахождение параметров уравнений линий регрессии у на х и х на у производится путем решения соответствующих систем нормальных уравнений. Для линейного случая существует еще один, упрощенный способ. Вид уравнений линейной, параболической и показательной регрессий и способы расчета их параметров помещены в таблицу 10. 7. Точность построенной регрессионной модели определяется с помощью средней ошибки аппроксимации
при этом y и y* - соответственно эмпирическое и теоретическое (рассчитанное по модели) значение признака Y, соответствующее данному значению x признака X.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

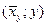 .
. и
и 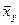 - групповые средние, которые определяются для каждого значения x признака X в первом случае и для каждого значения y признака Y во втором. Их расчетные формулы таковы:
- групповые средние, которые определяются для каждого значения x признака X в первом случае и для каждого значения y признака Y во втором. Их расчетные формулы таковы: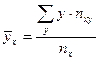 ,
, 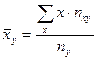 .
.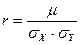 .
.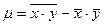 ,
,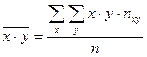 ,
,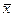 и
и  находятся по определению (задача 4) или методом моментов (задача 5); методом моментов (см. задачу 5)
находятся по определению (задача 4) или методом моментов (задача 5); методом моментов (см. задачу 5) .
.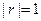

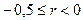
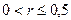
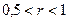
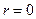
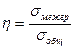 ,
,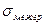 и
и  - соответственно межгрупповое и общее средние квадратические отклонения, равные
- соответственно межгрупповое и общее средние квадратические отклонения, равные ,
, 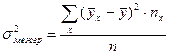 ,
,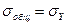 .
.
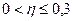
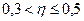



 .
.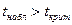 ,
,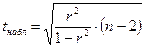 ,
,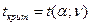 , α = 1- γ, ν = n – 2.
, α = 1- γ, ν = n – 2.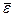 , равной
, равной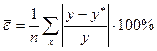 ,
,


