
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В частности, если тренд – линейный, тоСодержание книги
Поиск на нашем сайте
Параметры a и b могут быть найдены методом наименьших квадратов путем решения системы нормальных уравнений:
Решая ее, получаем:
Все необходимые расчеты делаем в таблице:
Получаем:
Итак, уравнение функции тренда имеет вид:
Задача 13. Построить индексы сезонности за 2008 год и за 2006 – 2008 г.г. Результаты представить графически. Помимо долговременных, на формирование значений уровней ряда динамики оказывают влияния сезонные факторы, определяющие периодическое изменение значений признака в определенные моменты времени (сезоны), причем эти изменения для каждого сезона можно считать постоянной величиной. Самым простым способом учета сезонных факторов является расчет индексов сезонности, которые для одного года равны:
при этом С целью избежания влияния случайных факторов, на практике, расчет индексов сезонности производится не за один, а за
Где
- среднее значение уровней ряда динамики, Соответствующих определенному сезону,
- среднее значение уровней ряда динамики за После того как значения индексов сезонности рассчитаны, результаты удобно представить графически в виде ломаной с вершинами в точках с координатами ( Рассчитываем значения индексов сезонности в таблице (обратить внимание на расчет средних значений, ряд – моментный!):
Точки, соответствующие индексам сезонности, рассчитанным по данным 2008 года, соединены пунктирной линией, а трем годам – сплошной. Задача 14. По данным о реализации продукции в 2008 году (см. задачу 11) построить математическую модель указанного ряда динамики. С учетом долговременных и сезонных факторов, математическая модель ряда динамики представляет собой композицию функцию тренда и индексов сезонности,
Используя результаты примера 12, имеем:
Задача 15. Смоделировать ряд динамики, характеризующий объем реализации продукции в 2008 году (см. задачу 11) в виде уравнения Фурье. Число гармоник взять равным 1, 2 и 3. Аналитическим подходом к учету сезонной и долговременной составляющих в ряде динамики, является моделирование его в виде уравнения Фурье (тригонометрического ряда):
При этом m – степень точности гармоники тригонометрического ряда; для различных значений m уравнение Фурье выглядит так (на практике берется не более четырех гармоник):
Величина
Коэффициенты уравнения Фурье находятся по формулам:
Все необходимые вычисления осуществляем в таблицах 14, 15 и 16. Таблица 14
Таблица 15
Таблица 16
Получаем:
Итак, уравнение Фурье в зависимости от числа гармоник имеет следующий вид:
Задача 16. Результаты задач 14 и 15 изобразить графически. По чертежу определить модель ряда динамики, по которой возможно построить наиболее точный прогноз. Для того чтобы построить график функции тренда, необходимо подставить в ее уравнения значения t = 1,2, …,12. Тем самым, для каждого месяца получаем значения Чтобы получить модель ряда динамики, необходимо каждое полученное ранее значение Для построения графика уравнения Фурье, необходимо для каждого значения t по таблицам 14 – 16 найти значения Все необходимые вычисления удобно производить в таблице 17. Строим чертеж (рисунок 16). Из рисунка следует, что наиболее точно описывает эмпирические данные модель Фурье, m = 3. Следовательно, по ней возможен наиболее точный прогноз.
Таблица 17
Рис. 16 Задача 17. По полученным моделям ряда динамики произвести прогноз реализации продукции в магазине на январь февраль и март 2009 года. Для того чтобы осуществить прогноз по модели ряда динамики необходимо:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.6.9 (0.009 с.) |

 .
. .
. .
.



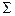
 ,
,  .
. .
.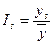 ,
, - значение уровня ряда динамики в момент времени в данный момент времени (сезон)
- значение уровня ряда динамики в момент времени в данный момент времени (сезон)  , а
, а  - среднее значение уровней ряда динамики.
- среднее значение уровней ряда динамики.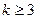 лет. В этом случае
лет. В этом случае ,
,

 лет.
лет. ;
;  ). Также на координатной плоскости удобно изобразить линию
). Также на координатной плоскости удобно изобразить линию  . С ее помощью можно увидеть, в каких случаях мы имеем значения ряда динамики ниже среднего уровня, а в каких – выше.
. С ее помощью можно увидеть, в каких случаях мы имеем значения ряда динамики ниже среднего уровня, а в каких – выше.




 .
. .
. .
.




 .
. ,
,  ,
,  .
.


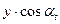

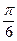









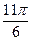










 ,
, ,
,  ,
,  ,
, ,
,  ,
,  .
.


 . Строим полученную прямую.
. Строим полученную прямую. ),
),  и
и  , которые затем подставляем в уравнение. Получаем
, которые затем подставляем в уравнение. Получаем 



