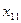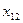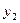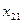Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Степень влияния факторного признака X на результативный признак Y определяется с помощью индекса детерминацииСодержание книги
Поиск на нашем сайте
Величины средней ошибки аппроксимации и индекса детерминации позволяют определить наиболее точную регрессионную модель. Ей считается та, у которой одновременно средняя ошибка аппроксимации стремится к минимуму, а индекс детерминации – к максимуму,
10. Прогноз значения у происходит путем подстановки данного значения х в уравнение регрессии у на х. Аналогично, для прогноза значения х по заданному значению у, необходимо использовать уравнение регрессии х на у. Таблица 10
Переходим к решению задачи. Вначале запишем исходные данные в виде корреляционной таблицы:
Строим корреляционное поле данных (рисунок 10)
Рис. 10 Производим все необходимые вычисления в ниже приведенной таблице. В клетке, стоящей на пересечении строки
Строим эмпирические линии (рисунок 11; на нем сплошной линией изображена эмпирическая линия регрессии у на х, а пунктирной – эмпирическая линия регрессии х на у) регрессии и делаем первоначальные выводы о форме корреляционной зависимости.
Рис. 11
Так как с ростом значения х значения у почти монотонно убывают, то скорее всего имеет место линейная обратная корреляционная зависимость. Определим величину коэффициента линейной корреляции. Среднее значение признаков найдем согласно определению, а дисперсии рассчитаем по формуле разностей. Имеем:
Среднее значение произведения
Тогда числитель коэффициента линейной корреляции, рассчитанный первым способом, равен:
Найдем величину μ методом моментов. Используя соответствующие определения и расчетную таблицу, получаем:
Итак, коэффициент линейной корреляции равен:
что говорит о том, что рассматриваемая зависимость является линейной обратной. Переходим к вычислению корреляционного отношения. Межгрупповая дисперсия равна
отсюда
Итак, корреляционное отношение равно
Найденное значение говорит о тесной корреляционной зависимости между рассматриваемыми признаками. Проверим с вероятностью 0,95 гипотезу о статистической значимости эмпирических данных. Наблюдаемое значение критерия Стьюдента равно.
Критическое значение находим по таблице 3 приложения для уровня значимости α = 1-0,95=0,05 и числа степеней свободы ν = 50 – 2= 48:
Имеем: 17,0664>2,02, следовательно гипотеза о статистической значимости эмпирических данных принимается с указанной вероятностью. Находим параметры регрессионных моделей (см. таблицу 10). Результаты вычислений представим в таблицах:
По каждой из полученных моделей находим величину средней ошибки аппроксимации и индекса детерминации (расчеты приведены в таблице 11). Имеем: для линейной модели
для параболической модели
для показательной модели
Видим, что одновременно минимум средней ошибки аппроксимации и максимум индекса детерминации соответствует линейной регрессионной модели. Следовательно, она признается наиболее точной. Графики линейной зависимости приведены на рисунке 12, параболической – на рисунке 13, а показательной – на рисунке 14. На них сплошной чертой изображены линии регрессии у на х, а пунктирной – х на у.
Строим прогноз признаков. Имеем: при стоимости основных производственных фондов 2,5 млн. руб., затраты на капитальный ремонт составят
Если затраты на капитальный ремонт составляют 0,52% от ОПФ, то стоимость основных производственных фондов должна составлять
Таблица 11
Рис. 12
Рис. 13
Рис. 14
Задача 10. Имеются следующие показатели по десяти предприятиям некоторой отрасли (на 31.12.2007):
Приняв стоимость основных промышленно – производственных основных фондов за результативный признак, а остальные показатели – за факторные признаки, необходимо:
а) исключив один из факторных признаков, перейти к двухфакторной регрессии; б) вычислить множественный коэффициент корреляции и сделать выводы о форме и силе корреляционной зависимости; в) с помощью F – критерия Фишера с вероятностью 0,95 оценить статистическую значимость эмпирических данных; г) вычислить значение общего индекса детерминации; д) двумя способами получить уравнение линейной модели множественной регрессии; е) по величине средней ошибки аппроксимации оценить точность линейной модели; ж) подсчитать дельта – коэффициенты; з) найти значения коэффициентов эластичности; и) исключить из модели один из факторных признаков и перейти к модели с парной регрессией.
1. Эмпирические данные выборки объема n принято записывать в виде таблицы, в которой Y – результативный признак со значениями
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.113.79 (0.01 с.) |

 .
. ,
,  .
.
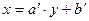


 ,
, 
 ,
, 
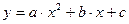

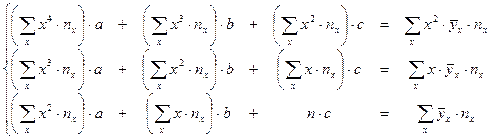




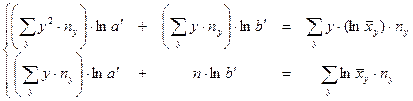
 Х
Y
Х
Y



 и столбца
и столбца 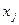 указаны следующие данные:
указаны следующие данные:

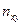













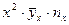




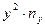





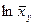




 ;
; ;
;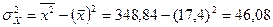 ;
;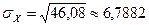 ;
; ;
; ;
;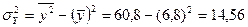 ;
; .
. .
. .
. .
. ,
, ,
, ;
; .
. .
.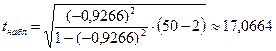 .
. .
.
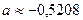 ,
, 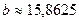
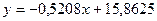

 ,
, 


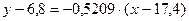 ,
,

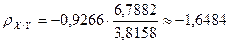
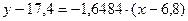 ,
,


 ,
,  ,
, 


 ,
,  ,
, 


 ,
,  ,
,
 ,
, 
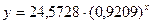

 ,
, 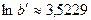 ,
,
 ,
, 

 ,
,  или 80,12%;
или 80,12%; ,
,  или 79,95%;
или 79,95%; ,
,  или 79,06%.
или 79,06%. (%).
(%). (млн. руб.)
(млн. руб.)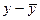


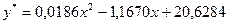




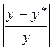



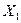 ,
,  ,…,
,…,  - факторные признаки со значениями
- факторные признаки со значениями  , i=1,2,…, n, j=1,2,… k:
, i=1,2,…, n, j=1,2,… k: