
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С помощью значений дельта – коэффициента и среднего коэффициента эластичности можно исключить из модели самый незначимый признак. Им признается тот, у которого одновременноСодержание книги
Поиск на нашем сайте
Решаем задачу. Вначале, запишем эмпирические данные (объем выборки n =10) в виде таблицы:
Все необходимые расчеты осуществлены в таблице 12. Под таблицей рассчитаем средние значения, дисперсии (по формуле разностей) и средние квадратические отклонения каждого из признаков.
Таблица 12
Y:
Теперь найдем средние значения произведений признаков:
Вычисляем межфакторные и парные коэффициенты линейной корреляции:
Займемся отбором факторных признаков в модель. Сначала с вероятностью 0,95 оценим статистическую значимость каждого из имеющихся факторных признаков. Согласно таблице 3 приложения критическое значение критерия Стьюдента для уровня значимости α = 1 - 0,95 = 0,05 и числа степеней свободы ν =10 – 2 = 8 равно
Вычислим наблюдаемые значения:
Видим, что только для признака Между признаками Множественный коэффициент корреляции равен:
С вероятностью 0,95 выдвинем гипотезу о статистической значимости эмпирических данных. Поскольку n = 10, k =2, то α =1-0,95 = 0,05
Наблюдаемое значение равно:
Правило проверки гипотезы выполнено. Поэтому с вероятностью 0,95 гипотеза о статистической значимости эмпирических данных принимается, корреляционная модель может быть построена. Общий индекс детерминации равен
Следовательно, факторные признаки, отобранные в модель, влияют на результативный в пределах 59,43%. Это не очень сильное влияние. Согласно закону Парето степень влияния должна быть не меньше 80%. Линейная модель, описывающая корреляционную зависимость, имеет следующий общий вид:
Используя таблицу 12, получаем систему нормальных уравнений:
Решая систему, получаем:
Итак, искомое уравнение регрессии имеет вид:
Найдем параметры уравнения регрессии упрощенным способом:
Найдем среднюю ошибку аппроксимации. Для этого, подставив значения факторных признаков, соответствующих данному значению y в модель, получаем теоретические значения y*. Вычисления производим в таблице:
Итак, значение средней ошибки аппроксимации равно
что говорит о низкой точности модели. Определим значения дельта – коэффициентов. Имеем:
Сумма дельта – коэффициентов равна 1, следовательно, есть все основания полагать, что вычисления произведены верно. Итак, признак Найдем величины средних коэффициентов эластичности:
Таким образом, изменение признака Перейдем к модели с парной регрессией. Поскольку одновременно минимум дельта – коэффициента и среднего коэффициента эластичности соответствует признаку
то он исключается из модели. Итак, общий вид уравнения парной регрессии следующий:
Так как
Для заметок
Тема 4. «Ряды динамики» Задача 11. Реализацияпродукции магазином (тыс. руб.) в 2006 – 2008 годах характеризовалось следующими данными (на конец месяца):
По данным 2008 года необходимо: а) определить тип ряда динамики; б) произвести анализ уровней ряда динамики цепным и базисным способами (за базисный принять уровень января 2008 года); в) найти средние значения уровней ряда динамики и его числовых характеристик. 1. Рядом динамики называется способ записи случайной величины (признака, фактора) Y, при котором ее значения (уровни)
2. Сравнение уровней ряда динамики производится двумя способами: цепным и базисным. При первом способе данный уровень основные показатели, характеризующие изменения уровней ряда динамики: абсолютный прирост, коэффициент роста, темп роста, темп прироста, абсолютное значение одного процента прироста (расчет этого показателя имеет экономический смысл только на цепной основе). Их расчетные формулы приведены в таблице:
3. В зависимости от типа ряда динамики среднее значение его уровней подсчитывается по формуле:
- если ряд динамики интервальный с равностоящими уровнями;
- если ряд динамики интервальный с неравноотстоящими уровнями,
- если ряд динамики моментный с равноотстоящими уровнями;
- если ряд динамики моментный с неравноотстоящими уровнями,
Среднее значение абсолютного прироста равно:
Величина среднего значения коэффициента роста равна:
Среднее значение темпов роста подсчитывается по формуле:
Наконец, среднее значение темпов прироста рассчитывается следующим образом:
Переходим к решению задачи. Так как значения уровней приведены на определенную дату (конец месяца), временная разность между уровнями постоянная (1 месяц), то рассматриваемый ряд динамики является моментным с равноотстоящими уровнями. Найдем числовые характеристики уровня ряда динамики. Результаты расчетов помещены в таблицу 13. В качестве примера произведем анализ строки таблицы 13, соответствующей октябрю месяцу. В октябре 2008 года магазин реализовал продукции на 523,2 тыс. руб., что на 27,8 тыс. руб. больше по сравнению с сентябрем и на 148,6 тыс. руб. больше по сравнению с январем 2008 года. Следовательно, реализация продукции в октябре увеличилась в 1,0561 раза по сравнению с октябрем и в 1,3967 раза по сравнению с январем. Уровень реализации в октябре составил 105,6116% от сентябрьского и 139,669% от январского уровня реализации. Таким образом, продукции в октябре реализовано на 5,6116% больше по сравнению с сентябрем и на 39,669% больше по сравнению с январем месяцем. Величина абсолютной величины одного процента прироста составила 4,954 тыс. руб.
Таблица 13
Найдем среднее значение уровней ряда динамики. Имеем: среднемесячный объем реализации продукции магазином составил в 2008 году
324,7 (тыс. руб.). Так как
то заключаем, что ежемесячное падение объемов реализации продукции в 2008 году составляло в среднем 9,1 тыс. руб. Среднее значение коэффициента роста равно
Это означает, что месячный уровень объема реализации составляет в среднем 0,972 от предыдущего месяца или (согласно формуле среднего значения темпов роста)
Итак, в среднем в месяц, объем продаж сокращался на 2,8% по сравнению с предыдущим месяцем, так как
Задача 12. По данным задачи 11 (рассмотреть данные 2008 года) построить уравнение линейной функции тренда. На формирование значение уровней ряда динамики основное влияние оказывают долговременные факторы, формирующие общую, в длительной перспективе тенденцию развития признака. Результат действия этих факторов моделируется в виде функции тренда
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |

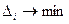 ,
,  .
.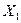








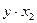






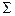
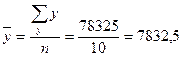 ,
,  ,
, ,
,  .
. ,
,  ,
, ,
,  .
.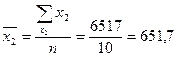 ,
,  ,
, ,
, 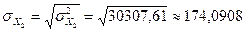 .
. ,
,  ,
, ,
,  .
. ;
; ;
; ;
; ;
; ;
; .
. ,
, ;
; ,
, ;
; ,
, ;
; ,
, ;
; ,
,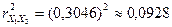 ;
; ,
, .
. .
. ;
; ;
; .
. , связь между ними тесная. Поэтому, один из этих признаков подлежит исключению. Поскольку
, связь между ними тесная. Поэтому, один из этих признаков подлежит исключению. Поскольку  >
>  , то признак
, то признак  Найденное значение указывает на высокую степень тесноты и линейности корреляционной зависимости.
Найденное значение указывает на высокую степень тесноты и линейности корреляционной зависимости. ,
,  . Согласно таблице 4
. Согласно таблице 4 .
. .
. .
. .
. ;
;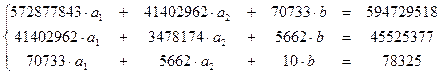 .
. ,
,  ,
,  .
. .
.
 ,
,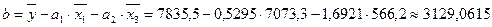 .
.
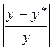
 ,
, или 91,54%,
или 91,54%, или 8,46%.
или 8,46%.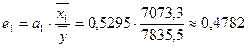 или 47,82%,
или 47,82%, или 12,23%.
или 12,23%. ,
, ,
, .
. , то согласно выводам задачи 9 связь признается линейной и тесной. Уравнение прямой линии регрессии найдем упрощенным способом (смотри п. 6 задачи 9):
, то согласно выводам задачи 9 связь признается линейной и тесной. Уравнение прямой линии регрессии найдем упрощенным способом (смотри п. 6 задачи 9): 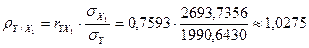 ;
; ;
; ;
;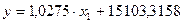 .
.
 приведены в зависимости от времени
приведены в зависимости от времени  . Если
. Если  - интервал времени (например, месяц, квартал, год и т. д.), то ряд динамики есть интервальный. Если же значения уровней приведены на определенную дату (например, начало месяца, конец квартала, начало года и т. д.), то ряд динамики есть моментный. Различают также ряды динамики с равноотстоящими и неравноотстоящими по времени уровнями. Ряд динамики принято представлять в виде таблицы:
- интервал времени (например, месяц, квартал, год и т. д.), то ряд динамики есть интервальный. Если же значения уровней приведены на определенную дату (например, начало месяца, конец квартала, начало года и т. д.), то ряд динамики есть моментный. Различают также ряды динамики с равноотстоящими и неравноотстоящими по времени уровнями. Ряд динамики принято представлять в виде таблицы:




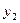

 сравнивается с предыдущем ему уровнем
сравнивается с предыдущем ему уровнем  . Во втором случае выбирается базисный уровень
. Во втором случае выбирается базисный уровень  (не обязательно первый) и все остальные уровни сравниваются с ним. Имеют место следующие
(не обязательно первый) и все остальные уровни сравниваются с ним. Имеют место следующие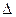




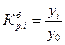


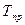



 или
или



 - временная разность между данным и следующим уровнем,
- временная разность между данным и следующим уровнем,  ;
;

 .
. .
.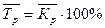 .
. .
.

 ,
,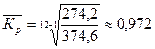 .
. .
. .
. .
.


