
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дополнительно вводим колонкуСодержание книги
Поиск на нашем сайте
Строим группированный статистический ряд.
Задача 2. По данным задачи 1 необходимо: а) построить полигон частот; б) построить гистограмму частот; в) построить кумулятивную кривую; г) по кумулятивной кривой определить вероятность p (19,7<X<23,55) попадания случайной величины в интервал (19,7;23,55) (то есть долю и процентное отношение числа элементов, находящихся в указанном интервале, к объему выборки). 1. Полигон частот есть ломаная с вершинами в точках с координатами 2. Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основания которых лежат на интервалах группировки, а площадь прямоугольников равна частоте соответствующего интервала. Исходя из определения заключаем: основание каждого из прямоугольников гистограммы равно b, а высота - 3. Кумулятивная кривая (или полигон относительных накопленных частот или кумулята) определяется как ломаная с вершинами в точках с координатами 4. Вероятность
где Строим полигон частот по колонкам 3 и 4 группированного статистического ряда (рисунок 4).
Рис.4 Строим гистограмму частот по колонкам 3 и 8 группированного статистического ряда из задачи 1 (рисунок 5). Строим кумулятивную кривую по колонкам 3 и 7 группированного статистического ряда из задачи 1 (рисунок 6). Используя определение и рисунок 6, получаем:
Итак, интервал (19,7;23,55) содержит около 81% элементов выборочной совокупности.
Задача 3. По данным задачи 1 найти а) моду, б) медиану, в) нижние и верхние квартили, децили, перцентили, г) сделать соответствующие выводы. 1. Модой называется значение признака, имеющее максимальную частоту. Интервал с нижней границей
где
Рис.5 2. Медианой группированного статистического ряда называется величина х, делящая вариационный ряд значений признака (то есть расположенных в порядке неубывания) на две равные по числу элементов части. Интервал с нижней границей
3. Квартили, децили и перцентили делят выборочную совокупность на 4, 10 и 100 равных по числу элементов частей. Различают верхние и нижние такие параметры. Их расчет и поиск интервала, их содержащих, аналогичен нахождению медианы:
- нижний параметр;
- верхний параметр, р равно 0,25 (квартиль), 0,1 (дециль), 0,01 (перцентиль).
Рис. 6 Составляем расчетную таблицу. В ней выделяем первые отрицательные разности и по ним смотрим интервалы, содержащие искомые параметры. Также выделяем максимальную частоту, которой соответствует модальный интервал. Напомним, что в рассматриваемой задаче объем выборки равен 100, а длина каждого интервала группировки равна 1.
Получаем:
Делаем выводы. 1. Наиболее часто встречающийся диаметр детали в выборочной совокупности составляет 21,1 мм. 2. В интервале (18;21,32) находится 50% деталей с минимальной величиной диаметра, а в интервале (23,32;26) – 50% деталей с максимальной величиной диаметра. 3. В интервалах (18;20,41), (18;19,64), (18;18,33) находятся соответственно 25%, 10% и 1% деталей с минимальным значением признака, а такая же доля деталей с максимальным значением признака принадлежит интервалам (22,32;26), (23,4;26), (25,75;26).
Задача 4. Для выборки из задачи 1 найти среднее значение и показатели вариации (среднее линейное отклонение, дисперсию, расчет которой произвести двумя способами, то есть по определению и по формуле разностей, среднее квадратическое отклонение, коэффициент вариации, асимметрию и эксцесс). Согласно соответствующим определениям, имеем:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.152.183 (0.008 с.) |

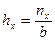 .
.
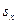
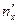
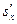
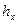
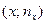 .
.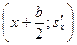 .
.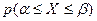 попадания случайной величины в интервал (α;β) находится следующим образом:
попадания случайной величины в интервал (α;β) находится следующим образом: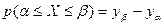 ,
,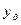 и
и 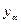 - ординаты точек кумулятивной кривой, абсциссы которых раны β и α соответственно.
- ординаты точек кумулятивной кривой, абсциссы которых раны β и α соответственно.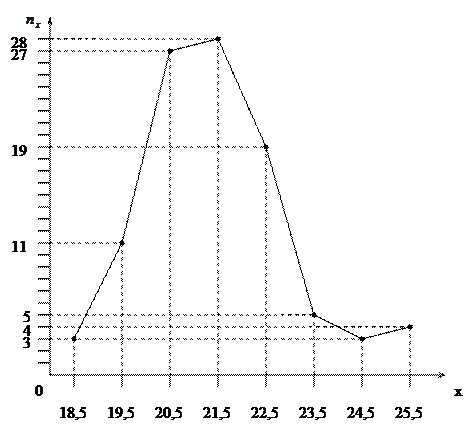
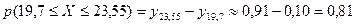 или 81%.
или 81%.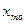 , длиной
, длиной 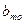 и частотой
и частотой 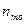 есть модальный (содержащий моду), если его частота – максимальна. Величина
есть модальный (содержащий моду), если его частота – максимальна. Величина 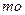 моды для группированного статистического ряда равна:
моды для группированного статистического ряда равна: ,
,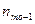 и
и 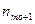 - частоты интервала, предшествующего и следующего за модальным соответственно.
- частоты интервала, предшествующего и следующего за модальным соответственно.
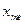 , длиной
, длиной 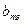 и частотой
и частотой 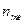 - медианный (содержит медиану), если для него первый раз, начиная от первого интервала, величина разности между полусуммой частот
- медианный (содержит медиану), если для него первый раз, начиная от первого интервала, величина разности между полусуммой частот 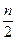 и накопленной частотой
и накопленной частотой 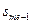 - накопленная частота интервала, предшествующего медианному, то медиана
- накопленная частота интервала, предшествующего медианному, то медиана  равна:
равна: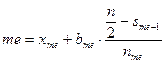 .
.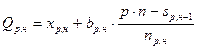
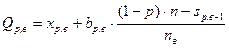





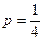
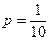
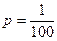
 (мм);
(мм);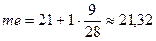 (мм);
(мм);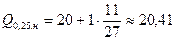 (мм),
(мм), 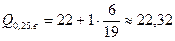 (мм);
(мм);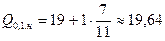 (мм),
(мм),  (мм);
(мм);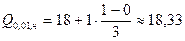 (мм),
(мм), 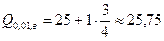 (мм).
(мм).


