Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интенсификация интеллекта и языки программированияСодержание книги
Поиск на нашем сайте Развиваемая в этой книге концепция улучшения работы ума опирается на гипотезу максимизации мозговой продуктивности (см. гл. 3). Исходя из этой гипотезы мы предполагаем, что главное (хотя и не единственное) средство для обеспечения гарантоспособной деятельности и предотвращения будущих технических и социальных чернобылей — совершенствование человеческого интеллекта [17]. Однако некоторые авторы считают проблему улучшения интеллекта некорректной и надуманной, поскольку “за всю историю развития человеческой цивилизации не отмечено сколь-нибудь заметное совершенствование человеческого интеллекта” [18]. На наш взгляд, подобное возражение основывается на недоразумении: ведь мы говорим не о генетически заданных предпосылках развития мышления (геном человека, как предполагают ученые, действительно не меняется на протяжении последних тысячелетий), а о механизмах социального наследования и передачи знаний и связанных с ними приобретенных возможностях интеллекта, которые можно значительно усилить. Предпринятое нами изучение проблемы улучшения работы ума есть развитие давней научной традиции, в рамках которой в связи с отсутствием устоявшейся терминологии разные ученые используют следующие сходные по смыслу, хотя и не полностью совпадающие понятия и выражения: “расширение способностей ума” (Декарт), “улучшение наших умозаключений”, “облегчение процесса нашего мышления” (Лейбниц); “усиление человеческого мышления” (Шредер), “облегчение мышления и придание ему большей точности и силы” (Фреге), “улучшение понимания” (Вертгеймер), “усиление мыслительных возможностей” (Брунер), “усиление природных психических процессов” (Верч), “увеличение КПД функционирования человеческого мозга”, “возрастание эффективности человеческого мышления”, “усиление знаниепорождающих, творческих функций естественного интеллекта человека”, “качественная интенсификация массового научного творчества” (Зенкин). Уместно привести мнение академика А. Ершова: “Человек неизмеримо усилит свой интеллект, если сделает частью своей натуры способность планировать свои действия, вырабатывать общие правила и способ их применения к конкретной ситуации, организовывать эти правила в осознанную и выразимую структуру, — одним словом, сделается программистом”. Ясно однако, что задача улучшения работы ума должна решаться не только применительно к программистам, но и к миллионам других людей. Известно, что “программист мыслит категориями, которые дает ему в распоряжение язык программирования” [19]. По мнению экспертов, влияние языка “независимо от нашего желания сказывается на нашем способе мышления” [20]. Язык оказывает глубокое воздействие “на навыки мышления и изобретательские способности”, причем “царящий в существующих языках беспорядок” непосредственно отражается на стиле и эффективности труда [19]. Чем определяется тот предел, до которого может усилить свой интеллект программист? Эта грань жестко регламентируется его личным интеллектуальным опытом и характеристиками тех языков, которые он использует в работе. Между тем все без исключения известные языки программирования наряду с многочисленными достоинствами имеют существенный недостаток — это кастовые языки ограниченного применения. Они не в состоянии обеспечить необходимое облагораживающее воздействие на интеллектуальную жизнь общества, преодолеть раздробленность индивидуальных интеллектов и обеспечить необходимое усиление могущества всемирного коллективного разума, соответствующее новым требованиям. Улучшение работы ума — проблема Наряду с классом языков программирования (которые, разумеется, должны продолжать функционировать в культуре) необходимо создать класс принципиально новых языков, для обозначения которых предлагается термин “суперязыки интеллектуального общения” (для краткости — суперязыки). Одно из наиболее драматических противоречий нынешней фазы развития цивилизации состоит в следующем. С одной стороны, немощь разума ставит под угрозу судьбу цивилизации, причем наука не имеет ответа на вопрос: как получить необходимый для спасения прирост интеллекта? С другой стороны, громадные интеллектуальные резервы человеческого мозга по-прежнему не используются, потому что люди “эксплуатируют” свой мозг из рук вон плохо, неграмотно, совсем не так, как того требуют его “проектные” (эргономические и нейробиологические) характеристики. Итак, зачем нужны суперязыки? Чтобы устранить это противоречие, преодолеть нынешний интеллектуальный тупик за счет выявления и научно-обоснованного использования скрытых резервов мозга. Социальный успех любого искусственного языка, его укорененность в культуре, возможность крупномасштабного расширения сферы его применения и международного признания зависят от общедоступности и полезности языка. Полезность суперязыков определяется тем, что они должны облегчить понимание и взаимопонимание, обеспечить стратегический интеллектуальный прорыв, позволяющий качественным образом увеличить умственную мощь цивилизации. Можно ли решить подобную задачу в принципе? Строго говоря, доказательный ответ на этот вопрос пока отсутствует. Вместе с тем можно высказать некоторые предположения. Письменный язык — это система нотаций, а нотация есть “средство мышления” [21]. Анализируя проблему улучшения нотаций, известный английский логик, математик и философ Альфред Норт Уайтхед пишет: “Освобождая мозг от всей необязательной работы, хорошая нотация позволяет ему сосредоточиться на более сложных проблемах и в результате увеличивает умственную мощь цивилизации” [21]. Обобщая вышеизложенное, можно сделать ряд замечаний. ! Способность или неспособность человечества решать жизненно важные глобальные, локальные и иные проблемы прямо зависит от эффективности всемирного разума и его локальных компонентов, от качества средств представления и формализации знаний, языковых средств понимания и взаимопонимания, удовлетворяющих критерию сверхвысокого понимания, эргономическому критерию Декарта. ! Чернобыль и другие инциденты со всей ясностью обнажили беспомощность нынешних форм планетарного интеллекта и поставили вопрос о разработке нового поколения интеллектуальных средств — суперязыков, способных обеспечить качественно новый уровень человеческого ума. ! Традиционные технократические методы разработки крупномасштабных промышленных объектов и социальных нововведений полностью исчерпали свои возможности, устарели и должны уступить место новым социотехническим методам, которые подразумевают системный подход к проектированию социосферы, техносферы и гарантоспособной человеческой деятельности. Выводы 1. Языки программирования играют заметную роль в человеческой культуре, являясь составным элементом компьютерной революции, которая, в свою очередь, есть необходимое условие перехода к информационному обществу. Наряду с этим все больше ощущается потребность в суперязыках, которые предназначены для кардинального улучшения работы ума, облегчения понимания и взаимопонимания, обеспечения более эффективного интеллектуального взаимодействия между людьми и в конечном итоге — улучшения человеческой деятельности (как теоретической, так и практической). 2. Некоторые суперязыки могут выполнять функции языков программирования, другие — нет. В роли суперязыков могут выступать только эргономичные визуальные языки. 3. 4. Выяснилось также, что языки программирования не могут обеспечить требуемый прирост интеллектуальной силы человеческих коллективов (локальных и глобальных). Из-за своего кастового характера и узости социальной базы языки программирования очень слабо влияют на улучшение коллективной работы ума в масштабах общества, на рост могущества социального интеллекта. Фактически они продемонстрировали свою непригодность для решения этой задачи. 5. Суперязыки должны сделать то, чего не могут языки программирования: стимулировать стратегический интеллектуальный прорыв, в максимально возможной степени увеличить умственную мощь человечества, обеспечить качественно новый уровень понимания и взаимопонимания и на этой основе — гарантоспособность планетарной и локальной человеческой деятельности. 6. Первым и, к сожалению, пока единственным примером суперязыка является техноязык ДРАКОН. Создание остальных суперязыков — дело будущего. Возможно, они будут появляться в результате эволюции (в сторону большей наглядности, доступности и общезначимости) графических языков новейших модификаций методологии RAD и CASE -технологий. Возможны и другие варианты. ДРАКОН — это всего лишь начальное звено в цепи суперязыков, которая обязательно должна наращиваться. 7. Язык ДРАКОН — это первый сознательно сделанный эргономический шаг в языковом строительстве. Эргономический — значит, во-первых, нацеленный на улучшение работы ума, во-вторых, опирающийся на всю мощь науки о человеческих факторах — эргономики и когнитивной науки. Сказанное можно резюмировать в форме краткого лозунга: ДРАКОН — это эргономическая революция в “языкостроении”. 8. Использование эргономики в языкостроении открывает перед этой наукой новые вдохновляющие перспективы, выявляет недостаточность нынешнего уровня эргономических знаний и требует дальнейшего развития ее идей. 9. Использование ДРАКОНА в качестве стандарта для описания структуры деятельности (как человеческой, так и делегированной) рассматривается как пробный шаг в направлении решения важнейшей цивилизационной задачи — проектирования гарантоспособной деятельности. Глава 19: Ученый, ты объясняешь нам науку, но кто объяснит нам твое объяснение? Джордж Байрон Почему Джойн фон Нейман провалился Математика — одна из разновидностей человеческой деятельности, поэтому логично поставить вопрос об эргономизации математики. Актуальность этой проблемы определяется следующим. Современная наука и система образования немыслимы без математики, но, к сожалению, математика чрезвычайно трудна и продолжает усложняться. Изучение математики требует колоссальных трудозатрат. Однако речь не только об учащихся. Появляющееся новое математическое знание стало столь разветвленным, что охватить его одному человеку или даже коллективу единомышленников (например, известной группе Николас Бурбаки) “физически невозможно”. Даже великий Джон фон Нейман признавался, что знает не больше чем 1/3корпуса математики и, чтобы проверить себя, попросил С. Улама проэкзаменовать его. Тот вспоминает: “Я устроил ему некоторое подобие докторантского экзамена в различных областях, стараясь выделить те вопросы, на которые он не мог бы ответить. Я нашел пробелы в дифференциальной геометрии, теории чисел, алгебре, где его ответы были неудовлетворительными” [1]. А ведь фон Нейман был выдающимся математиком! Но если трудности испытывают фигуры такого масштаба, с какими же поистине невероятными трудностями сталкивается подавляющее большинство математиков? Недаром говорят, что “в условиях современной математики математик не знает, как это ни парадоксально, математики” [1]. Что же тогда можно сказать о математических знаниях нематематиков и многочисленных армиях студентов? Проблема в том, что для большинства нематематических специальностей требования к математической подготовке постоянно возрастают, поскольку возрастает роль математики в современной науке и технике, теории и практике. В итоге получается, что люди не обладают знаниями, которые необходимы им для эффективного выполнения профессиональных обязанностей. Отпугивающая многих трудность изучения математики и вызванный ею недобор математических знаний неизбежно приводит к снижению интеллектуального потенциала общества, еще более усугубляя интеллектуальный кризис цивилизации. Попытка “запихнуть” в человеческую голову больше, чем она способна переварить за известный промежуток времени, ведет к экстенсификации учебного процесса, перегрузкам учащихся и педагогов, низкой эффективности обучения. Получается замкнутый круг, из которого в рамках традиционных подходов фактически нет выхода. Существует ли пропасть Чтобы преодолеть или хотя бы ослабить названные трудности, необходимо: ! улучшить понимаемость (когнитивное качество) математической литературы и за счет этого облегчить изучение математики; ! улучшить взаимопонимание между специалистами, работающими в разных отраслях и отделах математики (а их свыше трех тысяч [1]), а также в прикладных областях, тесно с нею связанных; ! уменьшить интеллектуальные усилия (интегральные умственные трудозатраты), которые общество расходует на изучение и решение математических проблем (при сохранении заданных стандартов качества).
Легко сообразить, что перечисленные задачи имеют эргономический характер. При разработке принципов эргономизации математики полезно учесть мировой опыт развития и комбинирования математической символики от древнейших времен до наших дней, но самое главное, уяснить, что эргономизация не есть нечто внешнее по отношению к математике. Как раз наоборот, эргономизация — это неотъемлемая внутренняя компонента исторического процесса развития математических идей. Тем не менее остается фактом, что сегодня эргономика и математика почти не имеют точек соприкосновения (применение математических методов в эргономике не в счет). Их разделяет пропасть взаимного непонимания. Другой удивительный факт состоит в том, что математики на протяжении всей истории применяли и применяют эргономические методы. Однако этот процесс носил и носит неосознанный, стихийный и кустарный характер, ощутимо снижая когнитивное качество математических текстов, ухудшая понимание и взаимопонимание в математическом сообществе. Грубо говоря, эргономическая беспечность (а если отбросить деликатность — эргономическая неграмотность) традиционных математических методов представляет собой одну из причин неоправданно высокого интеллектуального барьера, окружающего величественный дворец математической науки. Для обозначения этого барьера появился даже специальный термин — математический терроризм [2]. Мы исходим из того, что в наш междисциплинарный век пренебрежение к эргономическим методам следует признать устаревшим. К тому же оно вступает в противоречие с уроками истории. Чтобы сделать эту мысль более наглядной, проиллюстрируем ее на примере развития правил записи алгебраических уравнений, выбрав в качестве точки отсчета алгебру Диофанта. Алгебра Диофанта Греческий математик Диофант (III век нашей эры) был последним великим математиком античности. До него уравнения решались в словесной либо в геометрической форме. Он впервые использовал в алгебре буквенную символику. Но введенные им буквенные обозначения были сокращениями соответствующих математических терминов, а не алгебраическими символами в нашем понимании. Тем не менее новшества Диофанта имели революционный характер. Он ввел обозначения неизвестной величины, ее первых шести положительных и отрицательных степеней, отрицательные числа, знак “минус” и знак “равенство”. Благодаря этому Диофанту удалось получить ряд важных результатов. Он даже сумел предвосхитить подстановки Эйлера [3, 4]. Однако современному читателю символика Диофанта кажется странной, запутанной и очень непривычной. Попробуем запастись терпением и совершим небольшую прогулку по джунглям диофантовой алгебры, ограничившись одним-единственным вопросом: как Диофант записывал уравнения? Прежде всего, попытаемся выяснить: как будут выглядеть наши современные знаки
если их перевести на язык Диофанта? Ответ дает табл. 8. Таблица 8
Таблица 9
Для обозначения чисел Диофант использует общепринятую у греков символику [5] (табл. 9). Греческие числа образуют непозиционную десятичную систему: как
При записи свободного члена уравнения Диофант сначала ставит символ М° (признак свободного члена), а затем его числовое значение (табл. 11). Таблица 10
Таблица 11
С учетом сказанного приведем несколько примеров записи уравнений в символике Диофанта. Обратите внимание: чтобы избавиться от нуля, во втором и третьем примерах Диофанту пришлось перенести свободный член в правую часть уравнения (табл. 12). Таблица 12
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.015 с.) |

 Проблема создания суперязыков приобрела особую актуальность в последнее время, когда выявилась жесткая связь между интеллектом и выживанием и несостоятельность традиционных методов интеллектуальной работы.
Проблема создания суперязыков приобрела особую актуальность в последнее время, когда выявилась жесткая связь между интеллектом и выживанием и несостоятельность традиционных методов интеллектуальной работы. ,
,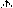





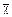















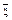



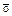





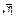




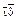 , так и
, так и  может значить только 14. Отсутствие позиционной системы вносит большие когнитивные затруднения: задача 4 × 10 = 40 (
может значить только 14. Отсутствие позиционной системы вносит большие когнитивные затруднения: задача 4 × 10 = 40 ( ) у греков не имеет ничего общего с “родственной” задачей
) у греков не имеет ничего общего с “родственной” задачей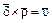 ). По этому поводу немецкий психолог Фридхарт Кликс восклицает: “Насколько проще метод нашей позиционной системы, насколько меньше затрат при решении одинаковых задач!” [5].
). По этому поводу немецкий психолог Фридхарт Кликс восклицает: “Насколько проще метод нашей позиционной системы, насколько меньше затрат при решении одинаковых задач!” [5]. Каждый член уравнения Диофант пишет так: сначала указывается степень неизвестного, потом числовой коэффициент; перед отрицательными членами ставится знак недостатка (по-нашему, минус), перед положительным — ничего (плюсом Диофант не пользуется) (табл. 10).
Каждый член уравнения Диофант пишет так: сначала указывается степень неизвестного, потом числовой коэффициент; перед отрицательными членами ставится знак недостатка (по-нашему, минус), перед положительным — ничего (плюсом Диофант не пользуется) (табл. 10).