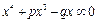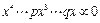Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эргономический анализ алгебры ДиофантаСодержание книги
Поиск на нашем сайте
Попытаемся оценить способ записи уравнений, использованный Диофантом, с точки зрения современных когнитивных представлений. Не претендуя на составление полной “дефектной ведомости”, укажем лишь несколько эргономических недостатков диофантовой алгебры. 1. Когда человек смотрит на запись уравнения, он должен решить несколько визуальных задач, обеспечивающих правильное зрительное восприятие и понимание сути дела, причем сделать это “без излишней траты умственных сил”. Первая задача — разбить зрительную сцену на два главных смысловых блока (левую и правую части уравнения). Для этого нужно выполнить три зрительных операции: ! бегло просмотрев все символы уравнения, найти среди них знак равенства; ! сделать вывод: зрительная зона, находящаяся левее этого знака, есть левая часть уравнения; ! сделать вывод: зона, лежащая правее, есть правая часть.
Современный знак равенства “=” с пробелами до и после него имеет удачную эргономическую конфигурацию, как нельзя лучше подходящую для этой цели. По форме он резко отличается от других знаков и эффектно “разламывает” уравнение на две части, благодаря чему человеческий глаз моментально решает первую визуальную задачу. Что касается алгебры Диофанта, то греческая буква иота i, используемая как знак равенства, слишком невзрачна и невыразительна — она теряется среди других букв. Из-за этого зрительное выделение и опознание двух частей равенства заметно усложняется.
В последней формуле присутствуют три пары из двух смежных букв. Все они трактуются по-разному, что создает неоправданную нагрузку на память человека: ! запись ! запись ! запись
Столь сложные правила расшифровки зрительной сцены вносят дополнительные и никому не нужные трудности в процесс зрительного восприятия. 3. Три класса объектов (неизвестные, цифры и операции) имеют сходные обозначения (всюду — буквы), что затрудняет визуальное различение указанных классов и кристаллизацию соответствующих понятий. 4. Не существует обозначений для нуля, плюса и степеней неизвестной выше шестой. 5. Степени неизвестной величины обозначаются не путем вариации одного знака (x, x 2, x 3, x 4, x 5, x 6), но имеют неоправданные различия и отсутствие общих элементов. В итоге нет визуальной подсказки, облегчающей опознание и выявление “родственных черт” у сходных понятий (степеней). 6. Отсутствует единая символика для чисел и показателей степени. Например, цифра 3 обозначается через Проведенный анализ показывает, что по эргономическим показателям символика Диофанта значительно уступает современным обозначениям. Эргономизация алгебры Алгебра Диофанта для своего времени была крупнейшим достижением. Однако ее постигла печальная участь. Оригинал на греческом языке в Европе был утерян и вновь найден только в XV веке [4]. К счастью, идеи Диофанта получили распространение в арабском мире и вернулись в Европу кружным путем — через арабское культурное влияние. При этом многое было утеряно и переоткрыто заново. Важным этапом на пути эргономизации европейской алгебры была замена греческих цифр на арабские. Самый древний европейский манускрипт, содержащий эти десять цифр, — “Вигиланский кодекс”, написанный в Испании в 976 г. Однако по ряду причин, которых мы не касаемся, арабская система счисления распространялась в Европе очень медленно и стала общепринятой лишь к 1500 г. [6]. К сожалению, имело место и попятное движение. Целый ряд эргономических находок Диофанта на несколько столетий был забыт. В частности, оказалась утраченной его буквенная символика, уступившая место словесным описаниям. Например, Леонардо Пизанский (1180—1240) называет неизвестную res (вещь) или radix (корень), квадрат неизвестной — census (имущество) или quadratus (квадрат); данное число — numerus. Все это — латинские переводы соответствующих арабских слов [6]. Наваждение слов преследовало математиков многие века. Поскольку не существовало символов даже для самых простых арифметических действий, каждый автор по-своему записывал сложение и вычитание, возведение в степень и извлечение корня. Требовалось немало усилий, чтобы разобраться в таком сложном переплетении форм записи. Поэтому ученые доверяли больше словам, чем знакам, тяготели больше к словесным описаниям, чем к формулам.
Смысл уравнения ясен из переводной табл. 13. Обратите внимание: в данном случае явное обозначение для неизвестной величины отсутствует — она в уравнении не записывается, а только подразумевается! Это серьезный эргономический недостаток. Есть и другой дефект: окончание подкоренного выражения никак не обозначено — его надо запоминать, что создает неоправданную нагрузку на память читателя. Таблица 13
Однако двинемся дальше. В 1489 г. в учебнике арифметики Яна Видмана впервые в печатном издании появились символы + и –, введенные чуть раньше немецкими алгебраистами (коссистами). Франсуа Виет (1540—1603) придумал знаки для произвольных величин, называемых сегодня параметрами, и предложил правило: неизвестные обозначать гласными буквами, а параметры — согласными (табл. 14). Таблица 14
A cubus + B in A 7 aequatur C Последнее выражение можно легко понять с помощью переводной табл. 15. Нетрудно видеть, что запись уравнений у Виета неэргономична, громоздка и словообильна. Таблица 15
aaa – 3. baa + 3. bba = 2. bbb Следующее эргономическое новшество принадлежит Рене Декарту. Он обозначил неизвестные величины буквами х, у, z, а известные — буквами a, b, c и ввел обозначения степеней: х 3, х 4, а 3, а 4. Правда, квадраты он иногда выражал с помощью символов xx, aa. Обозначение корня несколько отличается от современного: знак Осознание полезности Подведем некоторые итоги. Эргономизация алгебры очень важна. Как отмечает голландский историк математики Дирк Стройк, “новые результаты часто становятся возможными лишь благодаря новому способу записи... Подходящее обозначение лучше отображает действительность, чем неудачное, оно оказывается как бы наделенным собственной жизненной силой, которая в свою очередь порождает новое. За усовершенствованием алгебраических обозначений Виета поколение спустя последовало применение алгебры к геометрии у Декарта” [6]. С ним согласен В. Катасонов: «Весь XVI век проходит под знаком настойчивых поисков удобной (читай — эргономичной!) алгебраической символики, которая позволила бы создать некое “исчисление” для решения задач... без излишней траты умственных сил, механически следуя простым правилам». Суть эргономизации алгебры не только и не столько в том, что она выработала очень компактные и достаточно удобные обозначения, но прежде всего в том, что эргономичные знаки и (что самое главное) их эргономичные комбинации образуют эргономичные зрительные сцены (диосцены), которые точно и строго отражая математическую реальность, вместе с тем гораздо лучше согласуются с нейробиологическими характеристиками человеческого глаза и мозга, что создает важные предпосылки для улучшения творческой продуктивности человеческого ума. Известно, что “прогресс науки... связан с созданием и совершенствованием символики. В свою очередь, сам этот прогресс зависит от того, насколько компактна и совершенна та знаковая система, которая отображает существенные свойства и черты реальности” [7]. Конечно, каждый отдельно взятый символ не может играть слишком большой роли. Но вся совокупность символов в целом, взаимоотношения между которыми складываются по вполне определенным правилам, — это уже целый язык, новая знаковая система. В таком едином ансамбле знакам присущи новые эргономические и иные свойства, которых не имеет каждый из них в отдельности. Эргономическая сущность замены словесных описаний на эффективные и компактные алгебраические формулы состоит в том, что происходит “удивительная рационализация визуального поля” [7]. В результате в оптическом поле одномоментного восприятия, визуального охвата оказывается значительно большая информация в удобной и доступной для восприятия форме. Это означает, что имеет место эффект симультанизации, который, как мы знаем, является одним из наиболее мощных рычагов, обеспечивающих ускорение работы мозга. Согласно взглядам Лазаря Карно, математические знаки “не являются только записью мысли, средством ее изображения и закрепления, — нет, они воздействуют на саму мысль, направляют ее и бывает достаточно переместить их на бумаге согласно известным, очень простым правилам, чтобы безошибочно достигнуть новых истин”. Логика знаковых преобразований наталкивает людей “на глубокие, не всегда привычные взаимосвязи явлений” [7]. Кроме того эргономизация алгебры включает в себя все ходы мысли, связанные с дроблением и вычленением новых понятий, доведением их до логического совершенства. Приведем пример. Алгебра Декарта неэргономична еще и потому, что он использовал неудачное определение понятия “коэффициент”, полагая, что все буквенные коэффициенты в алгебраических формулах положительны. Это ограничение имело вредные последствия. Например, если p > 0 и q > 0, уравнение в записи Декарта полностью отвечает современным требованиям и является вполне эргономичным (если забыть про неудачный знак равенства):
Если же знак коэффициента произволен, Декарт вводит странные многоточия [4]:
Эти никому не нужные многоточия, усложняющие символику, являются следствием неудачного определения понятия “буквенный коэффициент”. Чтобы устранить недостаток, надо улучшить определение, т. е. сделать его более эргономичным. Для этого будем считать, что буквы в уравнениях обозначают любое действительное число[27]. При таком определении нелепые многоточия становятся ненужными и исчезают, превращаясь (как и положено) в знаки + и –. Данный пример показывает, что эргономизация понятий в свою очередь может оказывать благотворное влияние на эргономичность обозначений.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.013 с.) |

 2. Следующая визуальная задача — разбить каждую часть уравнения на смысловые блоки, т. е. выделить и опознать члены уравнения. Сегодня мы решаем эту задачу, фиксируя взором зрительные зоны, расположенные между знаками сложения и вычитания. Последние, выполняя функцию разделителей, моментально расчленяют уравнение, превращая его в гирлянду, состоящую из отдельных членов, “склеенных” с помощью символов + и –. У Диофанта дело обстоит гораздо хуже. Использование знака в качестве минуса трудно признать удачным. А полное отсутствие знака “плюс” — это уже бедствие, которое приводит к визуальной неоднозначности.
2. Следующая визуальная задача — разбить каждую часть уравнения на смысловые блоки, т. е. выделить и опознать члены уравнения. Сегодня мы решаем эту задачу, фиксируя взором зрительные зоны, расположенные между знаками сложения и вычитания. Последние, выполняя функцию разделителей, моментально расчленяют уравнение, превращая его в гирлянду, состоящую из отдельных членов, “склеенных” с помощью символов + и –. У Диофанта дело обстоит гораздо хуже. Использование знака в качестве минуса трудно признать удачным. А полное отсутствие знака “плюс” — это уже бедствие, которое приводит к визуальной неоднозначности. В самом деле, современное выражение х 2 + 3 х по Диофанту записывается так:
В самом деле, современное выражение х 2 + 3 х по Диофанту записывается так: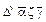
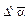 обозначает х 2;
обозначает х 2;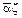 обозначает операцию сложения, причем в записи складываются члены
обозначает операцию сложения, причем в записи складываются члены 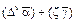 ;
;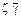 обозначает умножение х ´ 3.
обозначает умножение х ´ 3. , а x 3— через
, а x 3— через 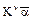 , но в последнем выражении цифра 3 отсутствует.
, но в последнем выражении цифра 3 отсутствует. Однако мало-помалу формульная запись начала пробивать себе дорогу. Но, Боже, что это были за формулы! Например, уравнение
Однако мало-помалу формульная запись начала пробивать себе дорогу. Но, Боже, что это были за формулы! Например, уравнение  записывалось в XV веке во Франции таким образом [7]:
записывалось в XV веке во Франции таким образом [7]: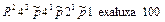
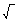
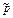
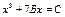
 В табл. 14 planum и solidum — паразитные слова, которые можно безболезненно опустить[26]. Сделав это, получим
В табл. 14 planum и solidum — паразитные слова, которые можно безболезненно опустить[26]. Сделав это, получим Тем не менее дело потихоньку двигалось вперед. Английский математик Р. Рекорд (1510—1558) придумал знак равенства =. Томас Гарриот (умер в 1621 г.) сделал следующий эргономический шаг, полностью исключив словесные описания. Уравнение
Тем не менее дело потихоньку двигалось вперед. Английский математик Р. Рекорд (1510—1558) придумал знак равенства =. Томас Гарриот (умер в 1621 г.) сделал следующий эргономический шаг, полностью исключив словесные описания. Уравнение  в записи Гарриота имело “почти современный” вид
в записи Гарриота имело “почти современный” вид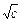 означает у Декарта кубический корень. Есть и другие недостатки: Декарт “испортил” знак равенства, изображая его как µ [4].
означает у Декарта кубический корень. Есть и другие недостатки: Декарт “испортил” знак равенства, изображая его как µ [4].