Переключатель и переключающий цикл

Предположим, в алгоритме нужно организовать разветвление на несколько направлений. Задачу можно решить двумя способами: с помощью иконы “вопрос” (рис. 46 а) и с помощью переключателя (рис. 46 б).

Переключатель — составной визуальный оператор (рис. 2, макроикона 3), имеющий один вход и один выход, содержащий одну икону “выбор” и несколько (две и более) икон “вариант” (рис. 1, иконы И5, И6). Внутри иконы “выбор” делается надпись, обычно в утвердительной форме, которая обозначает вопрос, имеющий строго определенное число ответов (два и более). Ответы записываются в иконах “вариант”. Таким образом, число вариантов равно числу ответов. Говоря формально, в иконе “выбор” записывается переменная, в иконах “вариант” — ее значения. На рис. 46 б переменная “Светофор” принимает три значения: зеленый, желтый, красный.

Переключатель позволяет создать особый тип цикла — переключающий цикл (рис. 2, макроикона 5). Для этого нужно оторвать выход правой ветви переключателя, загнуть его вверх и присоединить стрелку в нужное место (рис. 47).

На рис. 48 изображен цикл с переключателем, однако это не переключающий цикл, а обычный. Как их отличить? В первом случае переключатель имеет два выхода, во втором — только один. Есть еще одно отличие. Если вверх загибается выход иконы “вопрос” — это обычный цикл (ДО, ПОКА или гибридный). А если кверху идет выход переключателя — перед нами переключающий цикл.

Цикл Для

На рис. 49 и 50 показаны два варианта решения простой математи­ческой задачи. В первом случае используется цикл ДО, во втором — цикл ДЛЯ. Цикл ДЛЯ — составной визуальный оператор (рис. 2, макроикона 6), содержащий иконы “начало цикла ДЛЯ” и “конец цикла ДЛЯ” (рис. 1, иконы И12, И13), между которыми располагаются одна или несколько других икон. Внутри иконы “начало цикла ДЛЯ” указываются переменная цикла, ее начальное и конечное значения и шаг. Порядок записи этих величин определяется выбранным вариантом текстового синтаксиса. На рис. 50 изображен вариант, по умолчанию принимающий, что шаг равен 1.

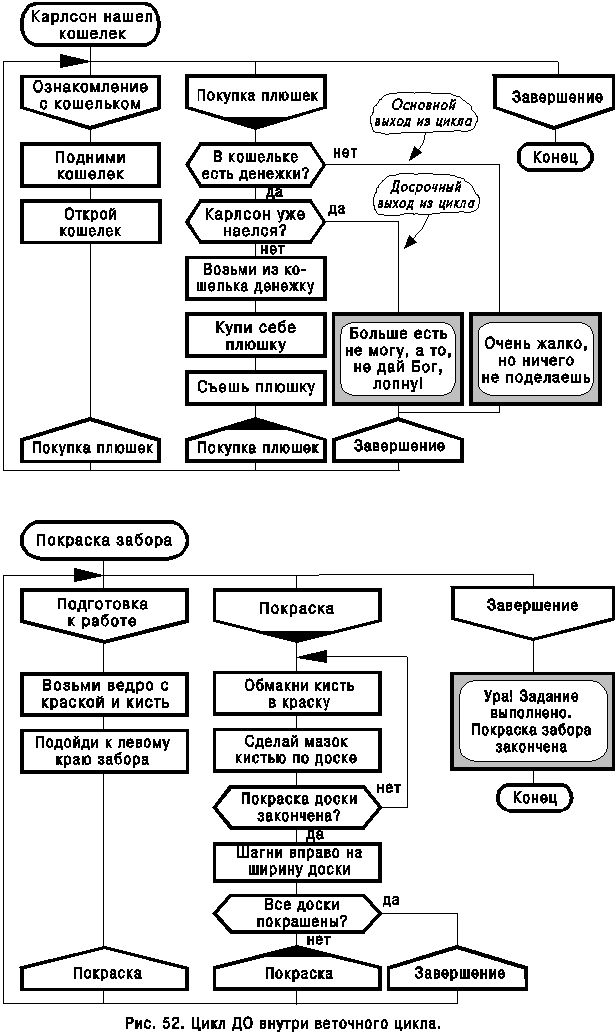
Веточный цикл

Циклы, описанные выше, могут использоваться как в примитиве, так и в силуэте. В этом параграфе речь пойдет о веточном цикле, который встречается только в силуэте.

Веточный цикл образуется, когда метка в иконе “адрес” указывает либо на свою ветку, либо на ветку, которая находится левее. Например, икона-адрес “Покупка плюшек” на рис. 51 указывает на свою ветку. Внутри веточного цикла могут появляться циклы других типов. На рис. 52 изображена конструкция “цикл в цикле”, у которой внутри веточного цикла находится цикл ДО.

При замене примитива на эквивалентный ему силуэт гибридный цикл нередко превращается в веточный цикл. В этом легко убедиться, сравнив эквивалентные алгоритмы на рис. 41 и 53.

Главный маршрут силуэта

В этом параграфе мы продолжим изучение веточных циклов и попытаемся ответить на вопрос: как найти главный маршрут веточного цикла? Для этого нужно проанализировать понятие “главный маршрут силуэта” (рис. 54).

Линейный (неразветвленный) силуэт имеет один-единственный маршрут, который и является главным. Он проходит по шампурам всех веток и по всем иконам силуэта (рис. 54 а).

Формула маршрута для силуэта имеет особенность: одноименные иконы “адрес” и “имя ветки” обозначаются одной буквой, которая повторяется в формуле дважды. Например, силуэт на рис. 54 а имеет формулу

 

где парные буквы обозначают переход с первой ветки на вторую (С — С) и со второй на третью (D — D).

Ветка называется одноадресной, если она имеет одну икону “адрес”. Если все ветки одноадресные, силуэт считается одноадресным.

Линейный силуэт всегда одноадресный. Однако одноадресный силуэт может быть и разветвленным. В последнем случае его главный маршрут следует по шампурам всех веток, однако он не проходит по всем иконам (рис. 54 б).

Если хотя бы одна ветка имеет более одного адреса, может сложиться ситуация, когда какие-то ветки не попадают на главный маршрут. На рис. 54 в икона-адрес D лежит на побочном маршруте. Это приводит к тому, что ветка D также оказывается на побочном маршруте. В результате главный маршрут проходит по шампурам всех веток, кроме ветки D (рис. 54 в).

Веточные циклы образуются только в многоадресных силуэтах, в одноадресных их в принципе не может быть. Они бывают нескольких типов:

! одноветочные (если цикл помещается в одной ветке);

! двухветочные (если цикл занимает две ветки);

! трехветочные (цикл в трех ветках)

и т. д.

Как работает одноветочный цикл? Предположим, до начала выполнения цикла на рис. 54 г имеют место условия

Предположим также, что веточный цикл выполняется два раза, после чего условие Е принимает значение “нет”. Это значит, что при третьем проходе по ветке В произойдет выход из цикла по пути “ Е нет С ”. В такой ситуации формула главного маршрута для силуэта на рис. 54 г принимает вид:

Как выглядит главный маршрут на дракон-схеме? Ответ изображен жирной линией на рис. 54 г. Мы видим, что главный маршрут как бы разветвляется в иконе Е и проходит через оба ее выхода. Разумеется, это условность, которая означает следующее. Сначала (когда Е = да) главный маршрут идет по шампуру, затем (когда выполняется условие окончания цикла Е = нет) главный маршрут проходит через правый выход иконы Е.

Чтобы построить одноветочный цикл, нужно в левой иконе “адрес” записать Х, где Х — имя данной ветки. Для выхода из цикла следует добавить вторую икону “адрес” и записать в ней Y, где Y — имя следующей (по порядку исполнения) ветки.

Если в веточном цикле слишком много икон, он может не поместиться в одной ветке. К счастью, его можно разделить на части. Например, веточный цикл на рис. 54 д содержит пять икон: Е, F, G, H, R (иконы “имя ветки” и “адрес” не в счет). Поместим иконы Е и F в ветку В, а иконы G, H, R — в ветку С. В результате цикл станет двухветочным. Главный маршрут силуэта с двухветочным циклом имеет разветвление в иконе R. Условие R = да позволяет вернуться к началу цикла. Если R = нет, главный маршрут ведет нас к концу алгоритма (рис. 54 д).

Таким образом, двухветочный цикл — это цикл, содержащий две ветки Х и Y, причем в ветке Х имеется икона-адрес Y, а в ветке Y — икона-адрес Х.

На рис. 54 е представлена ситуация “цикл в цикле”: веточный цикл С находится внутри веточного цикла В. Из рисунка видно, что в этом случае главный маршрут “разветвляется” дважды: в иконах R и J.

Если выполняется условие R = да, происходит повторение внутреннего цикла С. При сочетании условий производится выход из цикла С и повторение внешнего цикла В. Наконец, сочетание условий означает, что выполнение цикла В и алгоритма в целом заканчивается.

Выводы

1. В различных текстовых языках при описании циклов применяются разные наборы ключевых слов, имеющих к тому же разную семантику. Неразбериху усугубляют отличия в логике окончания цикла. Например, в языке Си для циклов while и do-while условие окончания цикла соответствует значению false или 0, условие продолжения — значению true или 1. В языке Паскаль картина иная: в цикле while-do выход из цикла соответствует значению false, а в цикле repeat-until по каким-то загадочным причинам применяется диаметрально противоположный принцип: выход из цикла производится, когда логическое выражение принимает значение true. Все эти путаные правила программист обязан знать и неукоснительно выполнять.

2. Отсутствие унификации ключевых слов и разнобой в определении условий выхода из цикла является серьезным недостатком: программисты вынуждены зубрить ключевые слова и значения условий, причем освоение каждого следующего языка требует новой зубрежки.

3. С точки зрения визуального программирования, указанные трудности являются надуманными и легко устраняются. Надо лишь отказаться от сложившихся привычек и устаревших стереотипов мышления, связанных с текстовым программированием. Визуализация качественно меняет ситуацию, поскольку текст больше не является единственным носителем информации.

4. Визуальные образы уменьшают нагрузку на память программиста, ликвидируют ошибки, вызванные неправильным пониманием семантики ключевых слов, отменяют ненужные ограничения, предоставляют пользователю богатую палитру выразительных средств и в конечном итоге обеспечивают более высокую понимаемость алгоритмов и программ.

5. Визуализация циклов — весьма полезный инструмент, так как сложные вложенные циклы со многими выходами часто бывают источником трудных ошибок. Многие из них возникают из-за путаницы, связанной с устаревшей привычкой описывать циклы словами. Сегодня никто не пытается заменить конструкторские и строительные чертежи словесными описаниями. По мнению автора, текстовая форма записи циклов во многих случаях является таким же анахронизмом, как словесное описание механического чертежа или электрической схемы.

 

Глава 9:
Визуализация логических
формул

Существует форма представления информации наглядная, броская, понятная всем с детства. Такой формой является графика.

Валерий Венда

Визуализация функции И

— Где можно купить щенка?

— В нашем городке они продаются на рынке, но сегодня рынок закрыт. К тому же щенков продают не каждый день. Щенки до­вольно дорогие и какие-то невзрачные — не знаю, понравятся ли они вам.

Из подслушанного разговора ясно, что покупка щенка возможна в том и только в том случае, когда выполняются четыре условия (рис. 55):

! рынок открыт (обозначим это условие через Р);

! у покупателя деньги есть (Q);

! щенки есть в продаже (R);

! щенок понравился (S).

 

В итоге получаем логическую функцию

 

где Х означает “Можно купить щенка?” (рис. 55).

В традиционных языках программирования значениями логических переменных считаются пары (ИСТИНА, ЛОЖЬ) или (1, 0). С эргономи­ческой точки зрения, такой подход нельзя признать удачным. В самом деле, использование “шибко мудреных” слов ИСТИНА и ЛОЖЬ или таинственных цифр 1 и 0 в примере о щенках (как и в любом другом конкретном примере) является надуманным, дезориентирующим и не содействует пониманию существа вопроса.

Чтобы поправить дело, в качестве значений логических переменных и логических функций гораздо лучше выбрать простые и ясные слова “да” и “нет”, семантика которых не требует пояснений и понятна даже ребенку. Исходя из этого, в языке ДРАКОН логические функции, переменные и выражения рассматриваются как да-нетные вопросы. Логическая функция И определяется как функция, которая принимает значение “да”, если все логические переменные имеют значение “да”. В остальных случаях функция приобретает значение “нет” (рис. 55)[17].

Существуют два способа изображения функции И на языке ДРАКОН: текстовый и визуальный. В первом случае используют одну икону “вопрос”, внутри которой пишут логическое выражение, состоящее из логических переменных, соединенных знаками логической операции И (рис. 56 слева). В другом случае на одной вертикали рисуют N икон “вопрос”, где N — число логических переменных, причем в каждой иконе записывают одну логическую переменную (рис. 56 справа).

Визуальная формула на рис. 56 показывает, что оба способа эквивалентны. Примеры на рис. 57 подтверждают это. Для практического использования рекомендуется визуальный способ, так как он более нагляден и позволяет быстрее найти ошибку в сложном алгоритме. Следует подчеркнуть, что текстовый способ не является запрещенным, но пользоваться им следует с осторожностью и лишь в тех случаях, когда пользователь убежден в своих способностях гарантировать отсутствие ошибок. Опыт показывает, что большинство людей выбирает визуальный способ как более легкий. Однако подготовленные специалисты, знакомые с основами математической логики, иногда предпочитают текстовый метод. Таким людям можно посоветовать освоить оба метода.

 

Визуализация функции ИЛИ

Логическая функция ИЛИ принимает значение “да”, если хотя бы одна логическая переменная имеет значение “да”. Функция принимает значение “нет”, если все логические переменные имеют значение “нет” (рис. 58).

На языке ДРАКОН функцию ИЛИ можно записать двумя способами. Если выбран текстовый способ, рисуют одну икону “вопрос”, содержащую логическое выражение (рис. 59 слева). При визуальном способе используют несколько икон “вопрос”, у которых объединяют нижний выход; в каждой иконе пишут одну логическую переменную (рис. 59 справа). Из рис. 59 и 60 видно, что оба метода эквивалентны.

Визуализация функции НЕ

Функция W = называется функцией НЕ, если логические переменные Z и W принимают инверсные значения, т. е. удовлетворяют условиям:

если Z = да, то W = нет;

если Z = нет, то W = да.

Визуальные формулы на рис. 61 показывают, что знак логического отрицания можно исключить из дракон-схемы, если поменять местами слова “да” и “нет” на выходах иконы “вопрос” (при этом иконы, находящиеся в плечах развилки, следует оставить на своих местах).

Упражнения на рис. 62—66 помогут читателю закрепить материал.