
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсорбцией называют процесс поглощения газов или паров из газовых или паро-газовых смесей жидкими поглотителями (абсорбентами).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При физической абсорбции поглощаемый газ (абсорбтив) не взаимодействует химически с абсорбентом. Если же абсорбтив образует с абсорбентом химическое соединение, то процесс называется хемосорбцией. Физическая абсорбция в большинстве случаев обратима. На этом свойстве абсорбционных процессов основано выделение поглощенного газа из раствора — десорбция. Сочетание абсорбции с десорбцией позволяет многократно применять поглотитель и выделять поглощенный компонент в чистом виде. В промышленности процессы абсорбции применяются главным образом для извлечения ценных компонентов из газовых смесей и для очистки этих смесей от вредных примесей перед их выбросом в атмосферу. При абсорбции содержание газа в растворе зависит от свойств газа и жидкости, давления, температуры и состава газовой фазы (парциального давления растворяющегося газа в газовой смеси). В состоянии равновесия при постоянных температуре и общем давлении зависимость между парциальным давлением газа А (или его концентрацией) и составом жидкой фазы для идеальных газов однозначна и выражается законом Генри - парциальное давление РА растворенного газа пропорционально его мольной доле ХА в растворе:
Или растворимость газа (поглощаемого компонента А) в жидкости при данной температуре пропорциональна его парциальному давлению над жидкостью
где Р*А - парциальное давление поглощаемого газа, находящегося в равновесии с раствором, имеющим концентрацию ХА (в мол. долях); Х*А - концентрация газа в растворе (в мол. долях), равновесном с газовой фазой, в которой парциальное давление поглощаемого компонента равно РА; Е - коэффициент пропорциональности, называемый коэффициентом, или константой Генри.
Числовые значения коэффициента Генри для данного газа зависят от природы поглотителя и газа и от температуры, но не зависят от общего давления в системе. Значения Е увеличивается с увеличением температуры, поэтому процессы абсорбции часто проводят при возможно низких температурах. Парциальное давление Р*А, согласно закона Дальтона равно:
где У*А – мольная доля А в газовой смеси, равновесной с жидкой фазой; Р - общее давление в системе
и тогда Отношение Е/Р = m называется коэффициентом распределения или константой фазового равновесия. При сильном разбавлении любой раствор приближается к идеальному, поэтому закон Генри применим только в области разбавленных растворов и на практике применяется для описания процесса абсорбции плохо растворимых газов. Для хорошо растворимых газов этот закон применим только при относительно низких концентрациях. При более высоких концентрациях растворимость газов обычно ниже, чем следует из закона Генри. Примером хорошо растворимых газов являются аммиак NH3, фтористый водород HF, хлористый водород HCl; умеренно растворимых – диоксид серы SO2, хлор Cl2; плохо растворимых – кислород, азот, углекислый газ. При химическом взаимодействии растворяемого газа с жидким абсорбентов процесс абсорбции называется хемосорбцией. При хемосорбции концентрация абсорбируемого компонент в жидкой фазе быстро уменьшается за счет образования нового химического соединения, что приводит к соответствующему увеличению движущей силы и интенсификации процесса абсорбции. В результате скорость процесса химической абсорбции зависит не только от скорости массообмена, но и от скорости химической реакции взаимодействия поглощаемого компонента и абсорбента. Адсорбция Механизм процесса адсорбции Адсорбцией называется концентрирование вещества в поверхностном слое в результате его самопроизвольного перехода из объема фазы. Процесс адсорбции обычно наблюдается в 2-х фазных системах: · Газ – твердое; · Жидкость - твердое. Равновесие в процессе адсорбции определяется двумя процессами: 1. Притяжением молекул (ионов) к поверхности раздела фаз под действием межмолекулярных сил. 2. Тепловым движением, стремящимся восстановить равенство концентраций в поверхностном слое и объеме фазы. Количественно процесс адсорбции характеризуется числом молей или массой вещества, накапливающегося на границе раздела фаз в расчете на единицу площади или объема твердой фазы. Фундаментальным вкладом в учение об адсорбции явилась теория Ленгмюра. Эта теория позволяет учесть ограниченность адсорбционного объема или поверхности адсорбента по поглощаемому веществу. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение является основным в теории Ленгмюра и уточняется следующими допущениями: 1) адсорбция локализована (молекулы не перемещаются по поверхности) на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбата - образуется мономолекулярный слой; 2) адсорбционные центры энергетически эквивалентны - поверхность адсорбента эквипотенциальна; 3) адсорбированные молекулы не взаимодействуют друг с другом.
Для получения уравнения изотермы обратимся к основному положению теории Ленгмюра. Примем, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:
А* + В ↔АВ*
где А* - адсорбционные центры на поверхности адсорбента; В – адсорбируемые молекулы; АВ* - образующийся на поверхности комплекс.
По мере увеличения концентрации вещества В реакция сдвигается в сторону образования комплекса и свободных адсорбционных центров становится меньше. Константа адсорбционного равновесия (без учета коэффициентов активности реагирующих веществ) равна:
В этом соотношении С*АВ=А и С*А =А∞ - А, (2) где А – величина адсорбции (количество поглощенного вещества на единице поверхности или массы адсорбента); А∞ - максимальная емкость адсорбционного слоя. Подставляя уравнение (2) в уравнение (1), получим:
или
После преобразований:
окончательно получим
Выражение (3) называется уравнением изотермы адсорбции Ленгмюра. Так как концентрации газов и паров практически пропорциональны парциальным давлениям, то для них изотерма адсорбции Ленгмюра принимает вид:
где РВ – парциальное давление вещества В в газовой смеси. Необходимо отметить, что константа адсорбционного равновесия в уравнении Ленгмюра (К и КР) характеризует энергию взаимодействия адсорбата с адсорбентом. Чем сильнее это взаимодействие, тем больше константа адсорбционного равновесия. Важны экстраполяционные следствия из соотношений (3) и (4). При малых концентрациях или давлениях, когда СВ ® 0, получаем: К×СВ ®0 и А = А¥×К×СВ Величина адсорбции линейно растет с увеличением концентрации. При больших концентрациях и давлениях, когда К×СВ >>1 и Кр×рВ >>1, уравнения (3) и (4) переходят в соотношение: А = А¥ (5)
Соотношения (5) отвечают насыщению, когда вся поверхность адсорбента покрывается мономолекулярным слоем адсорбата. При адсорбции газов из их смесей в соответствии с уравнением изотермы Ленгмюра величины адсорбции суммируются, а концентрация свободных центров является общей для равновесной многокомпонентной системы. В этом случае изотерма адсорбции для i –го компонента запишется следующим образом:
Из уравнения (6) следует, что увеличение парциального давления одного компонента подавляет адсорбцию других, и тем сильнее, чем больше его адсорбционная константа равновесия. Уравнение Ленгмюра можно использовать только при отсутствии адсорбции вещества сверх мономолекулярного слоя. Это условие выполняется достаточно строго при хемосорбции, физической адсорбции газов при небольших давлениях и температурах выше критической (при отсутствии конденсации на поверхности адсорбента), а часто и при адсорбции из растворов.
В большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй, третий и последующие адсорбционные слои. Эта возможность реализуется, когда газы и пары адсорбируются при температурах ниже критической, т. е. образуются полимолекулярные слои вещества на поверхности адсорбента, что можно представить как вынужденную конденсацию пара под действий поверхностных сил. В результате если в области образования мономолекулярного слоя величина адсорбции существенно замедляет свой рост с увеличением давления пара, то в области давлений, близкой к давлению насыщенного пара, она резко начинает возрастать и адсорбция заканчивается объемной конденсацией пара при p = ps (ps-давление насыщенного пара). Современная же форма уравнения полимолекулярной адсорбции — основного уравнения обобщенной теории Ленгмюра — была предложена лишь примерно двадцать лет спустя Брунауэром, Эмметом и Теллером. В соответствии с начальными буквами фамилий авторов обсуждаемая теория получила название теории БЭТ. В этой теории дополнительным допущением к тем, которые были положены в основу вывода уравнения изотермы Ленгмюра, является представление об образовании на поверхности адсорбента «последовательных комплексов» адсорбционных центров с одной, двумя, тремя и так далее молекулами адсорбата. Согласно теории БЭТ изотерма полимолекулярной адсорбции описывается уравнением:
где К – постоянная, равная отношению констант адсорбции и конденсации пара (константа конденсации пара величина обратная давлению насыщенного пара). К=Кр×рs При уменьшении парциального давления р/рs<<1
изотерма полимолекулярной адсорбции превращается изотерму Лэнгмюра (мономолекулярная адсорбция).
Скорость процесса адсорбции Процесс адсорбции в одних случаях может протекать очень быстро, в других - сравнительно медленно. Под кинетикой процесса адсорбции понимается изменение величины адсорбции А со временем τ: A=f(τ) dA/dτ=f’(τ)
Производная характеризует скорость адсорбции. Эти уравнения называют уравнениями кинетической кривой в интегральной и дифференциальной форме. Скорость адсорбции на однородной поверхности с образованием мономолекулярного слоя (ленгмюровская адсорбция) складывается из скоростей двух противоположных процессов. Скорость прямого процесса определяется скоростью закрепления молекул адсорбата на поверхности адсорбента V1, а обратного — скоростью удаления молекул с поверхности V 2. Первая скорость пропорциональна числу столкновений молекул адсорбата ν1 с единицей поверхности адсорбента, доле свободной поверхности (1—θ) и доле молекул α, способных к закреплению на поверхности. Скорость обратного процесса (десорбции) пропорциональна числу уходящих молекул ν2 с единицы площади насыщенной поверхности и степени заполнения поверхности θ. В результате скорость адсорбции выразится суммарным уравнением:
где ν0 – количество активных на единице поверхности адсорбента. После решения дифференциального уравнения получаем:
где кс – константа скорости адсорбции.
Рассмотрим, от каких факторов зависит константа скорости адсорбции Кс. Для Кс может быть записано следующее выражение, вытекающее из уравнения (7):
т.е. Кс пропорциональна скоростям процессов адсорбции и десорбции. Число столкновений молекул адсорбата ν1 с единицей поверхности адсорбента может быть определена с помощью выражения из молекулярно-кинетической теории:
где n – число молекул в единице объема; u – средняя скорость молекул в заданном направлении (из фазы к границе раздела); M – молекулярная масса; NA – число Авогадро; R – универсальная газовая постоянная; T – температура.
Число уходящих молекул ν2 с единицы площади насыщенной поверхности равно числу молекул, обладающих энергией Едес (энергия активации десорбции), достаточной для отрыва от поверхности, т. е. ν2 пропорционально фактору Больцмана:
Учитывая уравнение (8) можно записать:
Выражение (9) вместе с ранее полученными позволяет проанализировать зависимости константы скорости адсорбции от различных факторов.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.98.29 (0.011 с.) |


 ,
, ,
,

 (1)
(1)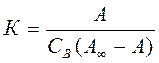


 (3)
(3) , (4)
, (4) (6)
(6) ,
,
 (7)
(7)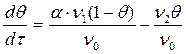
 или
или 
 , (8)
, (8) ,
,
 (9)
(9)


