
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При этом виде страхования нетто-премия вычисляется по формулеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
п -летнее смешанное страхование жизни
Нетто-премия вычисляется по формуле:
Полное страхование жизни, отсроченное на т лет
При этом виде страхования нетто-премия вычисляется по формуле:
п- летнее временное страхование жизни, отсроченное на т лет
Полное страхование жизни с непрерывно возрастающим пособием
19. Расчет нетто-премий при полном страховании жизни с выплатой страхового пособия в конце последнего года жизни. РАСЧЕТ НЕТТО-ПРЕМИЙ ДЛЯ ОСНОВНЫХ ДИСКРЕТНЫХ ВИДОВ СТРАХОВАНИЯ
Исходя из определения дискретных видов страхования, и понятия актуарной стоимости можно получить следующие формулы для вычисления нетто-премий: 1. Полное страхование жизни с выплатой страхового пособия в конце последнего года жизни. Нетто-премия вычисляется как
Где
является дискретным анализом непрерывной упрощающей функции
20. Расчет нетто-премий при п-летнем временном и смешанном страховании жизни с выплатой страхового пособия в конце последнего года жизни. п - летнее временное страхование жизни с выплатой пособия в конце года смерти
3. п - летнее смешанное страхование жизни с выплатой пособия в конце года смерти
где
4. Полное страхование жизни с выплатой страхового пособия в конце последнего года жизни, отсроченное на т лет
5. Полное страхование жизни с ежегодно возрастающем пособием и выплатой пособия в конце последнего года жизни
Обозначив
Здесь
21. Связь между непрерывным и дискретным видами страхования жизни.
Дискретное страхование жизни- страховая сумма выплачивается в конце года смерти. Вычисления можно проводить непосредственно по таблицам продолжительности жизни. Вычислив нетто-премии при дискретном страховании жизни, можно вычислить и нетто-премии при соответствующих видах непрерывного страхования. Для того чтобы связать между собой непрерывные и дискретные виды страхования необходимо сделать определенные предположения о законе распределения времени жизни для дробных возрастов. Обычно предполагают, что этот закон – равномерный. Известно, что в этом случае случайные величины
Приведенные выше формулы позволяют вычислять разовые нетто-премии по непрерывным видам страхования через характеристики
22.. Анализ суммарного иска в модели долгосрочного страхования жизни. Пусть в момент времени
и компания не разорится, если будет выполнено условие вида:
где
которая аналогична соответствующей формуле для краткосрочного страхования жизни. То есть расчет вероятности неразорения при долгосрочном страховании производится так же, как и при краткосрочном страховании с величинами убытков Тогда плата за страховку будет иметь вид:
где В простейшем случае, когда страховая надбавка делится пропорционально математическим ожиданиям, получаем:
При более сложных моделях долгосрочного страхования не всегда удается выразить: а) вероятность неразорения в виде простой формулы вида (32); б) нетто-премии и страховые надбавки в виде (34).
|
||||
|
Последнее изменение этой страницы: 2016-09-17; просмотров: 602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.247.78 (0.01 с.) |

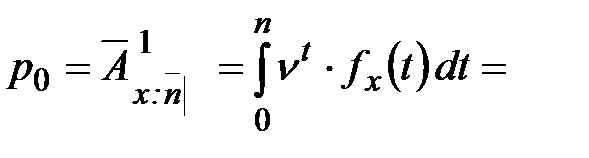
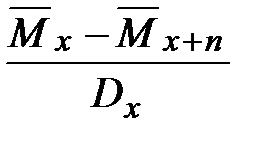 . (16)
. (16)
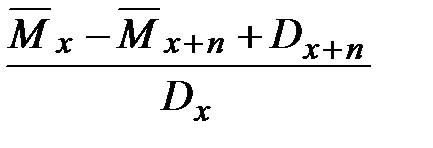 . (17)
. (17)
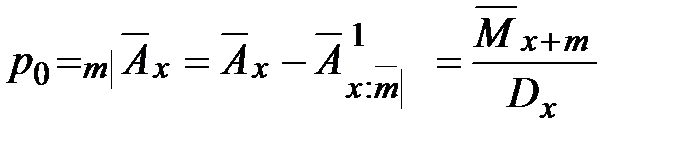 . (18)
. (18)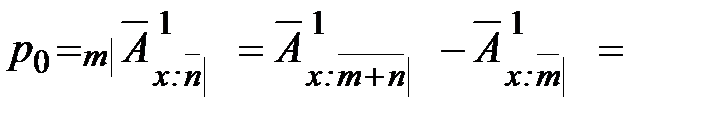
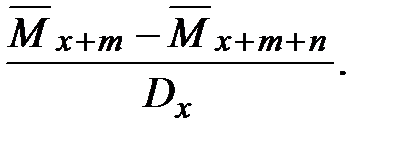 (19)
(19)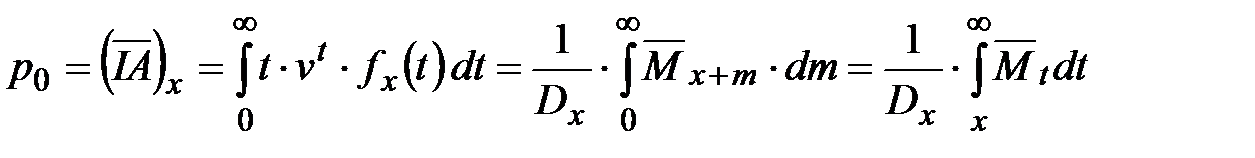 . (20)
. (20)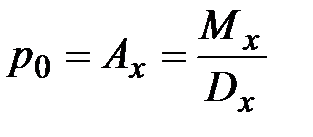 . (21)
. (21)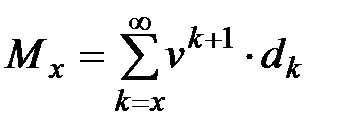 , (22)
, (22)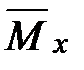 .
.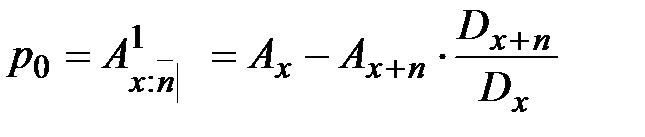 . (23)
. (23)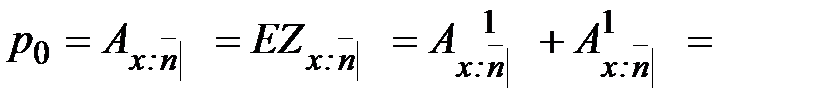
 . (24)
. (24) .
.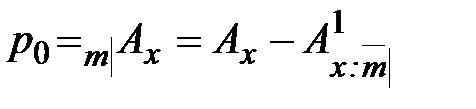
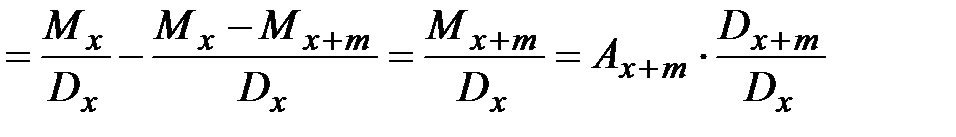 . (25)
. (25)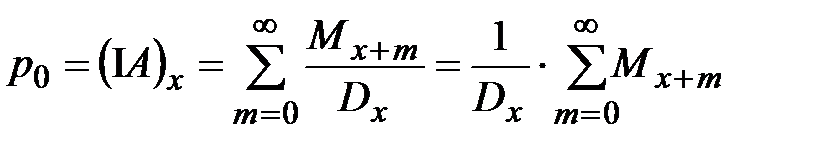 . (26)
. (26)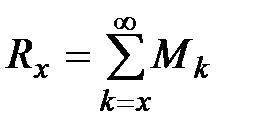 , можем записать
, можем записать  в виде
в виде .
.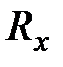 - это дискретная упрощающая функция.
- это дискретная упрощающая функция. и
и  независимы, и
независимы, и 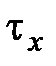 имеет равномерное распределение на
имеет равномерное распределение на 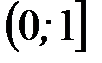 . Тогда можем получить следующие формулы, связывающие нетто-премии для соответствующих непрерывных и дискретных видов страхования:
. Тогда можем получить следующие формулы, связывающие нетто-премии для соответствующих непрерывных и дискретных видов страхования: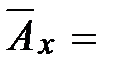
 . (27)
. (27)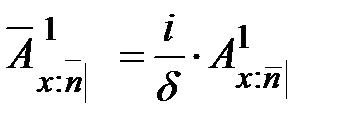 , (28)
, (28)
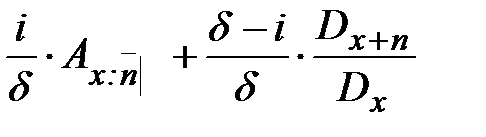 , (29)
, (29)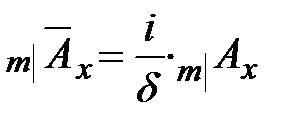 , (30)
, (30)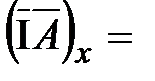
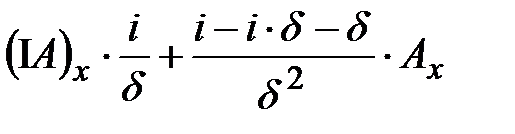 . (31)
. (31) ,
, 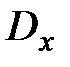 ,
, 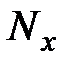 , которые достаточно просто вычисляются по данным, приводимым в общих таблицах продолжительности жизни.
, которые достаточно просто вычисляются по данным, приводимым в общих таблицах продолжительности жизни.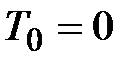 страховая компания заключила
страховая компания заключила  договоров страхования жизни. Обозначим через
договоров страхования жизни. Обозначим через 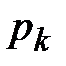 - премии, а через
- премии, а через  - величину страхового пособия, выплачиваемого по
- величину страхового пособия, выплачиваемого по  - ому договору в случайный момент времени
- ому договору в случайный момент времени 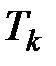 . Расположим величины
. Расположим величины  . Тогда в момент времени
. Тогда в момент времени  капитал компании можно вычислить как
капитал компании можно вычислить как ,
, ,
, - современная стоимость выплаты
- современная стоимость выплаты  по
по 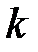 - ому договору страхования. Вероятность неразорения будет вычисляться по формуле:
- ому договору страхования. Вероятность неразорения будет вычисляться по формуле: , (32)
, (32)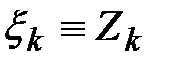 .
. , (33)
, (33)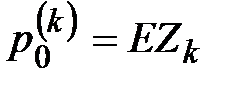 - нетто-премия по
- нетто-премия по 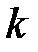 - ому договору, а
- ому договору, а 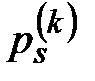 - соответствующая страховая надбавка, которая вычисляется аналогично краткосрочному страхованию жизни.
- соответствующая страховая надбавка, которая вычисляется аналогично краткосрочному страхованию жизни. . (34)
. (34)


