
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Таким образом, плотность распределения вероятностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вычисление платы за страховку
Пусть в компании застраховано
и вероятность разорения определяется как
В случае нормального распределения получаем
в плату за страховку включаtv некоторую надбавку То есть плата за страховку будет теперь иметь вид:
Тогда капитал компании будет равен
где Найдем вероятность неразорения компании
И если мы хотим, чтобы вероятность неразорения компании была равна
или
величина добавочной суммы Так как в выражение (12) входит среднее квадратическое отклонение
Распределение пропорционально ожидаемому убытку Разделим сумму
Просуммируем (13) по
или
и
Тогда
Здесь
относительная страховая надбавка.
Распределение пропорционально дисперсиям
Недостатком назначения индивидуальных премий по правилу (13) является то, что оно несправедливо по отношению к договорам, которые имеют малую дисперсию Поэтому можно разделить сумму
Просуммировав по
или
Отсюда
Следовательно,
и относительная страховая надбавка
Распределение пропорционально средним квадратическим отклонениям
Если же разделить сумму
то, просуммировав по
или
Отсюда следует, что
Следовательно,
и
С точки зрения страховой компании все равно, какое из трех правил (13), (15) или (17) применять для начисления надбавок
16. МОДЕЛИ ДОЛГОСРОЧНОГО СТРАХОВАНИЯ ЖИЗНИ
Долгосрочное страхование жизни, в отличие от краткосрочного страхования, характеризуется тем, что при расчетах принимают во внимание изменение стоимости денег с течением времени. Годовая процентная ставка, используемая при этом, носит название технической процентной ставки или технического процента. Технический процент выбирается страховщиком в таком размере, чтобы при самых неблагоприятных обстоятельствах обеспечить выбранную доходность инвестиций. Поэтому теория долгосрочного страхования существенно опирается на методы расчетов, рассматриваемых в финансовой математике.
Общую модель страхования определяют две функции: а) б) Величину страхового взноса с единицы страховой суммы называют тарифной ставкой или тарифом. .
Страхование с выплатой страхового пособия в конце года смерти
Здесь речь идет о дискретных аналогах,когда выплата пособия производится в конце года смерти застрахованного, то есть в момент времени а) дискретного полного страхования жизни:
б)
в)
г) полного дискретного страхования жизни, отсроченного на
д) полного страхования жизни с переменной страховой выплатой, например, с ежегодно возрастающим пособием
17. Принципы назначения нетто-премий. Полное страхование жизни.
Полное страхование жизни
Согласно формулам (1) и (9) получаем
и нетто-премия будет равна математическому ожиданию
Обозначив
А если ввести обозначение:
то
Функцию Для упрощения записи вводят и выражения:
тогда
Величины
18. Расчет нетто-премий при п-летнем чисто накопительном, временном и, смешанном
непрерывном страховании жизни. п -летнее чисто накопительное страхование жизни
Нетто-премия будет вычисляться как:
Если же в № 8 воспользоваться упрощающими функциями, то:
Видно, что аппроксимация законов продолжительности жизни моделью де Муавра несколько искажает результаты вычисления нетто-премий. п -летнее временное страхование жизни
ВИДОВ СТРАХОВАНИЯ
Исходя из определения дискретных видов страхования, и понятия актуарной стоимости можно получить следующие формулы для вычисления нетто-премий: 1. Полное страхование жизни с выплатой страхового пособия в конце последнего года жизни. Где
является дискретным анализом непрерывной упрощающей функции
20. Расчет нетто-премий при п-летнем временном и смешанном страховании жизни с выплатой страхового пособия в конце последнего года жизни. п - летнее временное страхование жизни с выплатой пособия в конце года смерти
3. п - летнее смешанное страхование жизни с выплатой пособия в конце года смерти
где
4. Полное страхование жизни с выплатой страхового пособия в конце последнего года жизни, отсроченное на т лет
5. Полное страхование жизни с ежегодно возрастающем пособием и выплатой пособия в конце последнего года жизни
Обозначив
Здесь
21. Связь между непрерывным и дискретным видами страхования жизни.
Дискретное страхование жизни- страховая сумма выплачивается в конце года смерти. Вычисления можно проводить непосредственно по таблицам продолжительности жизни. Вычислив нетто-премии при дискретном страховании жизни, можно вычислить и нетто-премии при соответствующих видах непрерывного страхования. Для того чтобы связать между собой непрерывные и дискретные виды страхования необходимо сделать определенные предположения о законе распределения времени жизни для дробных возрастов. Обычно предполагают, что этот закон – равномерный. Известно, что в этом случае случайные величины
Приведенные выше формулы позволяют вычислять разовые нетто-премии по непрерывным видам страхования через характеристики
22.. Анализ суммарного иска в модели долгосрочного страхования жизни. Пусть в момент времени
и компания не разорится, если будет выполнено условие вида:
где
которая аналогична соответствующей формуле для краткосрочного страхования жизни. То есть расчет вероятности неразорения при долгосрочном страховании производится так же, как и при краткосрочном страховании с величинами убытков
Тогда плата за страховку будет иметь вид:
где В простейшем случае, когда страховая надбавка делится пропорционально математическим ожиданиям, получаем:
При более сложных моделях долгосрочного страхования не всегда удается выразить: а) вероятность неразорения в виде простой формулы вида (32); б) нетто-премии и страховые надбавки в виде (34). Полная пожизненная рента
Простейшая пожизненная рента пренумерандо описывается следующим образом: начиная с момента времени Обозначим через х возраст человека в момент времени
которая является случайной величиной. Здесь Так как
поэтому расчет характеристик пожизненной ренты можно свести к расчету характеристик соответствующего дискретного страхования жизни. Найдем актуарную современную стоимость пожизненной ренты (нетто-премию):
или
Для расчета защитной надбавки
где Формула (4) получен методом суммарной выплаты, когда пожизненная рента рассматривается как сумма случайного числа если при страховании рент речь пойдет о ренте постнумерандо, когда страховые выплаты будут производиться в конце соответствующего периода, то вычисление современной стоимости будет производиться по формуле:
24. Временная пожизненная рента.
Временная п - летняя пожизненная рента выплачивается начиная с момента времени
Учитывая, что современная стоимость п – летнего дискретного смешанного страхования жизни определяется как:
получаем:
Поэтому современная актуарная стоимость такой ренты будет вычисляться как
где Для расчета защитной надбавки
Можем
25. Отсроченная пожизненная рента.
Отсроченная на m лет пожизненная рента представляет собой серию выплат единичной суммы, начиная с момента времени
Так как
то
Поэтому актуарная стоимость этой ренты будет равна
или
26. Актуарная современная стоимость и актуарная наращенная сумма.
некий пенсионный фонд, в который
Величину Следовательно, для получения единичной суммы в момент времени
Величина Коэффициенты
и
Тогда и введенные выше актуарные стоимости рент можно записать как
Здесь можно отметить, например, что
27. Пожизненные постоянные p - срочные ренты.
Ежегодные ренты,встречаются значительно реже, чем ренты, выплачиваемые несколько раз в год (полугодовые, ежеквартальные, ежемесячные).
Полная пожизненная рента
Полная пожизненная р – срочная рента пренумерандо описывается следующим образом: начиная с момента времени
Здесь
Тогда приведенная стоимость такой ренты в момент времени
а актуарная стоимость будет равна
Временная пожизненная рента
В этом случае период выплат будет ограничен некоторым сроком в n лет. То есть, если человек проживет еще n лет В предположении о равномерном распределении времени жизни для дробных возрастов можем получить следующую формулу для вычисления актуарной стоимости такой ренты
Здесь
Если в равенстве (17) перейти к пределу при
х - целое число лет.
28. Непрерывные пожизненные ренты.
Пусть в полной пожизненной ренте, выплачиваемой с частотой
С учетом того, что
Тогда актуарная приведенная стоимость такой ренты будет равна
Можем
В случае временной непрерывной пожизненной ренты платежи производятся не более, чем
а актуарная стоимость:
29. Схема расчета периодических нетто-премий. Периодические нетто-премии при полном дискретном страховании жизни. СХЕМА РАСЧЕТА НЕТТО-ПРЕМИЙ
Предположим, что страховая премия выплачивается в виде серии платежей в течение некоторого срока с момента заключения договора страхования. При такой периодической уплате взносов застрахованный выполняет свои обязательства в рассрочку. Однако стоимость обязательств компании не зависит от способа уплаты страховых премий. При расчете величины периодически уплачиваемых премий необходимо учитывать как процентный доход от инвестиций, так и демографические факторы (смертность). Последний фактор оказывает существенное влияние на величину взносов, так как не все застрахованные успевают уплатить все предусмотренные контрактом взносы. В общем виде, схема расчета нетто-премий может быть представлена следующим образом. Пусть
которое представляет собой условие равенства обязательств застрахованного и страховой компании на момент заключения договора страхования. Отметим, что, как и ранее, полная периодическая премия Применим теперь общую схему (1) к различным вариантам страхования.
Таким образом, плотность распределения вероятностей
она приближенно описывает долю умерших в возрасте от x до x +1 лет от исходной группы в График функции свойства функции f (x):
1. 2. 3. Таким образом, кроме
2.Интенсивность смерти.Макрохарактеристики продолжительности жизни. интенсивность смертности- э то величина, которая характеризует вероятность смерти в интервале
Статистическим аналогом интенсивности смертности
характеризующая долю тех представителей исходной группы, доживших до возраста x лет, которые умрут в течение ближайшего года. Для случайной величины
Для работы со случайной величиной В Приложении приведена общая или упрощенная таблица продолжительности жизни (aggregate tables), которая содержит информацию о статистических свойствах времени жизни случайно выбранного человека, относительно которого известен только его возраст. В таблицу включены следующие характеристики: а) б) в) г) д) е) В качестве шага таблицы рассматривается 1 год
Аналитический закон распределения- Де Муавр (1724 г.) постулировал существование максимального возраста
тогда
3.. Распределение остаточного времени жизни. Основные величины, связанные с оста- точным временем жизни При страховании жизни страхователь имеет дело с конкретными людьми, дожившими до определенного возраста x. Поэтому необходимо рассмотрение случайной величины
определяющей остаточное время жизни человека, дожившего до х лет. Закон распределения вероятностей этой случайной -
вероятность смерти человека, достигшего возраста x лет, в течение ближайших t лет. Дополнительная вероятность
это вероятность того, что человек в возрасте x лет проживет еще не менее В частном случае, при
вероятность того, что человек в возрасте х лет умрет в течение ближайшего года, и
вероятность того, что человек в возрасте х лет проживет, по крайней м
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-17; просмотров: 541; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.220.6 (0.015 с.) |

 человек. Возьмем в качестве платы по
человек. Возьмем в качестве платы по  - ому договору величину
- ому договору величину 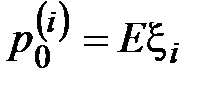 . Тогда резервный фонд (капитал) компании равен
. Тогда резервный фонд (капитал) компании равен ,
, .
. .
. , которая бы компенсировала элементы случайности
, которая бы компенсировала элементы случайности  .
.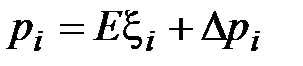 . (11)
. (11) ,
, .
. .
. , то
, то  должен быть равен квантилю
должен быть равен квантилю 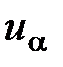 , то есть
, то есть ,
,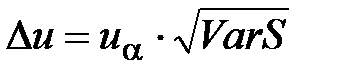 - (12)
- (12) .
. , то добавочная сумма
, то добавочная сумма  действительно учитывает риск, связанный с непредсказуемостью убытков.
действительно учитывает риск, связанный с непредсказуемостью убытков. пропорционально ожидаемому убытку
пропорционально ожидаемому убытку 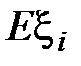 , то есть
, то есть . (13)
. (13) :
: ,
,
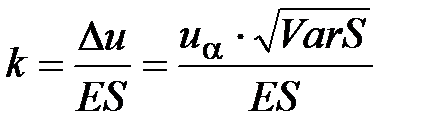 .
. . (14)
. (14) - нетто-премия,
- нетто-премия,  - страховая надбавка,
- страховая надбавка, - (14’)
- (14’) , и потому оплачивают в большей степени случайности, связанные с договорами с большей дисперсией.
, и потому оплачивают в большей степени случайности, связанные с договорами с большей дисперсией.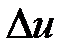 пропорционально дисперсиям:
пропорционально дисперсиям: . (15)
. (15)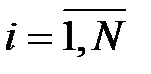 , получаем
, получаем ,
, .
. .
. (16)
(16) . (16’)
. (16’)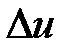 пропорционально средним квадратическим отклонениям:
пропорционально средним квадратическим отклонениям: , (17)
, (17) ,
, .
. .
.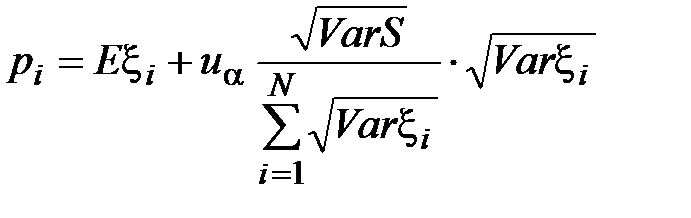 (18)
(18)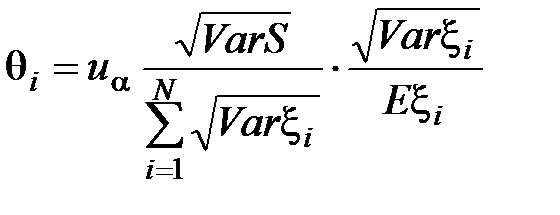 . (18')
. (18') , так как в любом случае она получит одну и ту же страховую сумму
, так как в любом случае она получит одну и ту же страховую сумму .
. - величина страхового пособия, выплачиваемого в момент времени
- величина страхового пособия, выплачиваемого в момент времени  наступления страхового случая;
наступления страхового случая;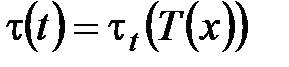 - момент выплаты страхового пособия – функция остаточного времени жизни застрахованного.
- момент выплаты страхового пособия – функция остаточного времени жизни застрахованного. . Тогда, для:
. Тогда, для: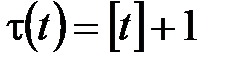 ,
,  ; (1´)
; (1´) - летнего дискретного временного страхования жизни:
- летнего дискретного временного страхования жизни: (3´)
(3´) - летнего дискретного смешанного страхования жизни:
- летнего дискретного смешанного страхования жизни: ,
, 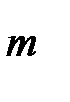 лет:
лет: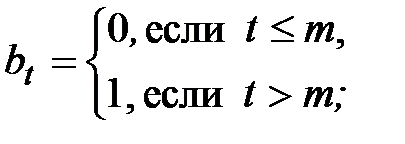 (5´)
(5´)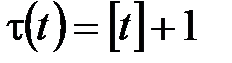 ,
,  . (7´)
. (7´) :
: , (10)
, (10) .
. , можем получить:
, можем получить: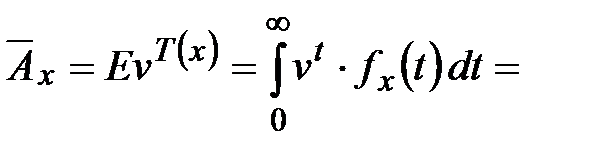
 .
. (11)
(11) .
. называют замещающей или упрощающей, используется также и термин – коммутационная функция.
называют замещающей или упрощающей, используется также и термин – коммутационная функция.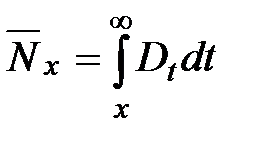 , (12)
, (12) , (13)
, (13) . (14)
. (14) и
и  также называются замещающими или упрощающими функциями. Они протабулированы в некоторых таблицах продолжительности жизни.
также называются замещающими или упрощающими функциями. Они протабулированы в некоторых таблицах продолжительности жизни.
 . (15)
. (15) (57,51%).
(57,51%).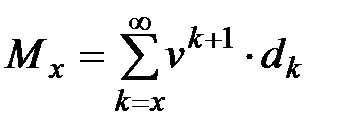 , (22)
, (22)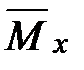 .
.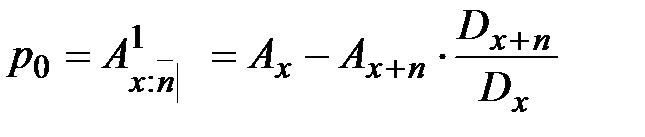 . (23)
. (23)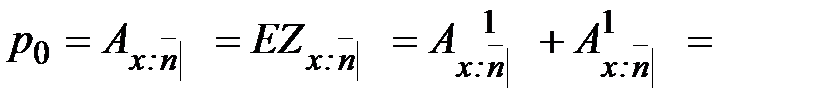
 . (24)
. (24) .
.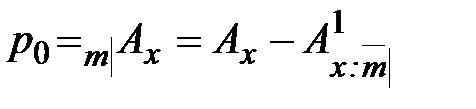
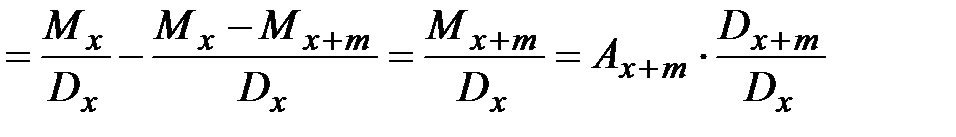 . (25)
. (25)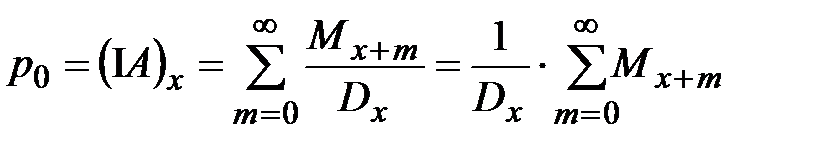 . (26)
. (26)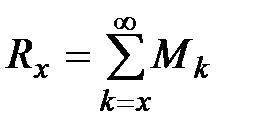 , можем записать
, можем записать  в виде
в виде .
.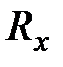 - это дискретная упрощающая функция.
- это дискретная упрощающая функция. и
и  независимы, и
независимы, и 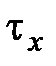 имеет равномерное распределение на
имеет равномерное распределение на 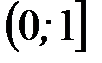 . Тогда можем получить следующие формулы, связывающие нетто-премии для соответствующих непрерывных и дискретных видов страхования:
. Тогда можем получить следующие формулы, связывающие нетто-премии для соответствующих непрерывных и дискретных видов страхования: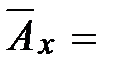
 . (27)
. (27)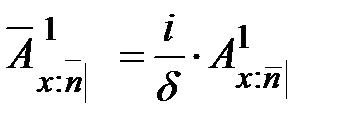 , (28)
, (28)
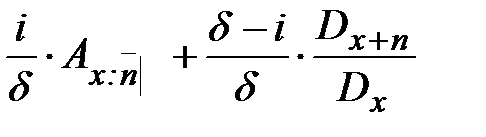 , (29)
, (29)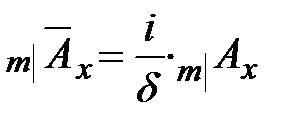 , (30)
, (30)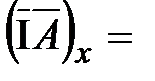
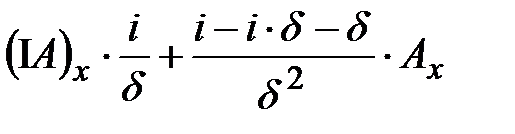 . (31)
. (31) ,
, 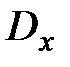 ,
, 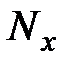 , которые достаточно просто вычисляются по данным, приводимым в общих таблицах продолжительности жизни.
, которые достаточно просто вычисляются по данным, приводимым в общих таблицах продолжительности жизни.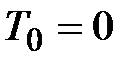 страховая компания заключила
страховая компания заключила  договоров страхования жизни. Обозначим через
договоров страхования жизни. Обозначим через 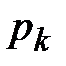 - премии, а через
- премии, а через  - величину страхового пособия, выплачиваемого по
- величину страхового пособия, выплачиваемого по  - ому договору в случайный момент времени
- ому договору в случайный момент времени 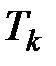 . Расположим величины
. Расположим величины  . Тогда в момент времени
. Тогда в момент времени  капитал компании можно вычислить как
капитал компании можно вычислить как ,
, ,
, - современная стоимость выплаты
- современная стоимость выплаты  по
по 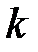 - ому договору страхования. Вероятность неразорения будет вычисляться по формуле:
- ому договору страхования. Вероятность неразорения будет вычисляться по формуле: , (32)
, (32)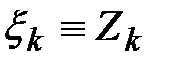 .
. , (33)
, (33)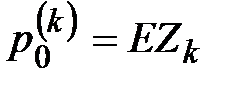 - нетто-премия по
- нетто-премия по 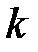 - ому договору, а
- ому договору, а 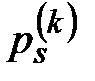 - соответствующая страховая надбавка, которая вычисляется аналогично краткосрочному страхованию жизни.
- соответствующая страховая надбавка, которая вычисляется аналогично краткосрочному страхованию жизни. . (34)
. (34) , человек один раз в начале каждого года начинает получать определенную постоянную сумму, которую примем в качестве единицы измерения денежных сумм. Выплаты этой суммы производятся только во время жизни человека.
, человек один раз в начале каждого года начинает получать определенную постоянную сумму, которую примем в качестве единицы измерения денежных сумм. Выплаты этой суммы производятся только во время жизни человека. , где
, где  - остаточная продолжительность жизни. То есть имеем дело с годовой рентой пренумерандо со случайным числом выплат
- остаточная продолжительность жизни. То есть имеем дело с годовой рентой пренумерандо со случайным числом выплат 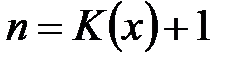 . Найдем современную стоимость такой ренты
. Найдем современную стоимость такой ренты , (1)
, (1)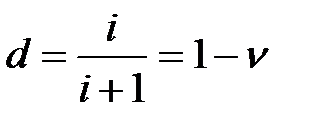 - годовая ставка дисконтирования.
- годовая ставка дисконтирования. - современная стоимость полного дискретного страхования жизни, то
- современная стоимость полного дискретного страхования жизни, то , (2)
, (2) , (3)
, (3)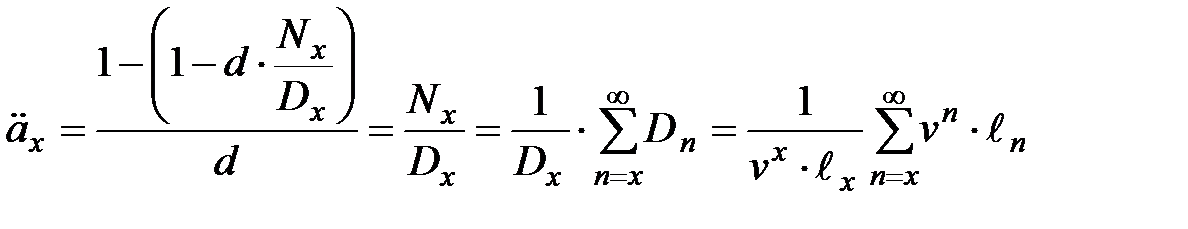 . (4)
. (4) и оценки вероятности разорения компании необходимо уметь вычислять и дисперсию
и оценки вероятности разорения компании необходимо уметь вычислять и дисперсию  , а именно
, а именно , (5)
, (5)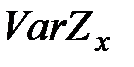 вычисляется так же, как и в предыдущей главе.
вычисляется так же, как и в предыдущей главе. детерминированных слагаемых. Можно применить и другой метод – метод текущего платежа, который рассматривает эту ренту как сумму детерминированного числа случайных слагаемых.
детерминированных слагаемых. Можно применить и другой метод – метод текущего платежа, который рассматривает эту ренту как сумму детерминированного числа случайных слагаемых. .
. (6)
(6)
 .
.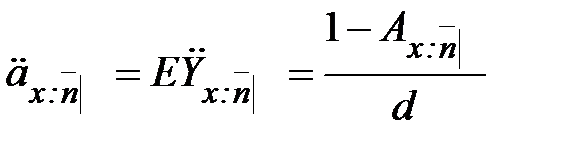 (7)
(7) - нетто-премия при дискретном смешанном страховании жизни.
- нетто-премия при дискретном смешанном страховании жизни. , а именно
, а именно .
. выразить и через характеристики жизни, рассмотренные ранее:
выразить и через характеристики жизни, рассмотренные ранее: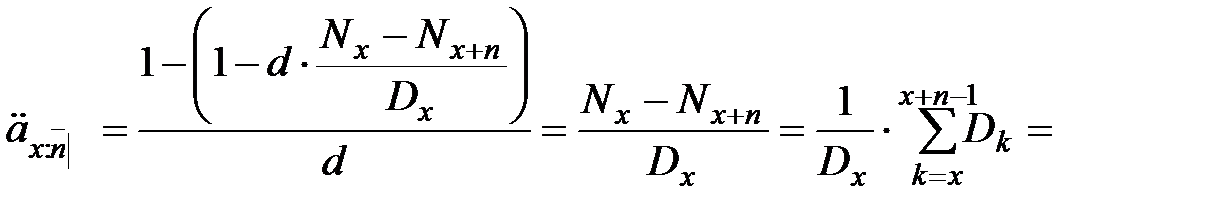
 , (8)
, (8) , до тех пор, пока человек жив. Тогда современная стоимость такой ренты равна
, до тех пор, пока человек жив. Тогда современная стоимость такой ренты равна (9)
(9)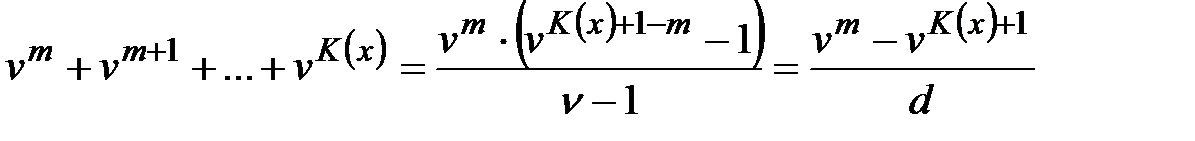 ,
, . (10)
. (10)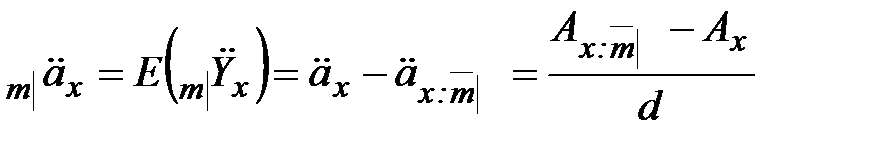 , (11)
, (11) . (12)
. (12)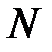 человек в момент времени
человек в момент времени  вносят по единичной сумме. К моменту времени
вносят по единичной сумме. К моменту времени 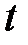 эта сумма возрастет до
эта сумма возрастет до 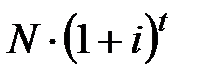 . Однако, если в момент времени
. Однако, если в момент времени  все
все  человек имеют возраст x лет, то к моменту времени
человек имеют возраст x лет, то к моменту времени 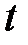 в живых останется в среднем
в живых останется в среднем  человек. Поэтому на каждого оставшегося в живых участника фонда будет приходиться сумма
человек. Поэтому на каждого оставшегося в живых участника фонда будет приходиться сумма . (13)
. (13) называют актуарным наращением или актуарным накоплением. Она больше обычного множителя наращения
называют актуарным наращением или актуарным накоплением. Она больше обычного множителя наращения 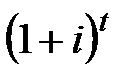 , так как происходит уменьшение числа живых участников фонда, претендующих на соответствующую им долю средств данного фонда.
, так как происходит уменьшение числа живых участников фонда, претендующих на соответствующую им долю средств данного фонда.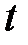 , каждый из
, каждый из 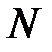 застрахованных должен внести в момент времени
застрахованных должен внести в момент времени 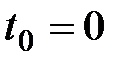 сумму
сумму . (14)
. (14)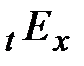 называется актуарным коэффициентом дисконтирования для человека в возрасте х на отрезке
называется актуарным коэффициентом дисконтирования для человека в возрасте х на отрезке  . Этот коэффициент, при равной величине выплат, всегда меньше современной стоимости обычной финансовой ренты, так как взносы по страховой ренте собираются со всех, а выплаты производятся только дожившим до сроков ее выплаты.
. Этот коэффициент, при равной величине выплат, всегда меньше современной стоимости обычной финансовой ренты, так как взносы по страховой ренте собираются со всех, а выплаты производятся только дожившим до сроков ее выплаты. и
и 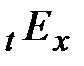 можно выразить и через упрощающую функцию
можно выразить и через упрощающую функцию  :
: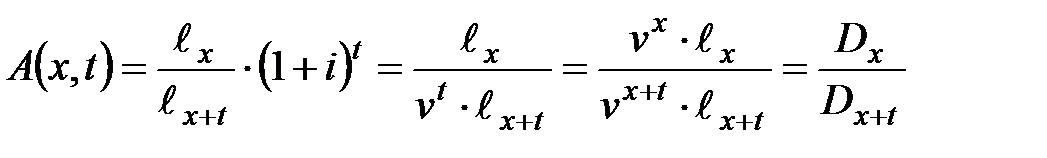 ,
, .
. ,
, ,
, .
. представляет собой среднюю сумму, которую надо внести, чтобы получить единичную сумму в каждый из моментов
представляет собой среднюю сумму, которую надо внести, чтобы получить единичную сумму в каждый из моментов  .
. лет будет получать
лет будет получать  раз в год по
раз в год по 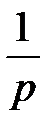 у.е. в начале каждой из
у.е. в начале каждой из  х долей года, то есть в моменты времени
х долей года, то есть в моменты времени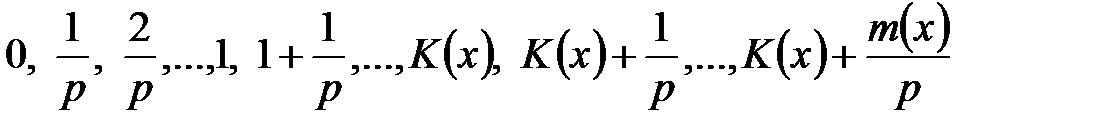 .
. - целое число из промежутка
- целое число из промежутка  такое, что
такое, что .
. будет вычисляться как
будет вычисляться как , (15)
, (15) . (16)
. (16) , то будет произведено
, то будет произведено  выплат; а если же человек умрет до достижения возраста n лет
выплат; а если же человек умрет до достижения возраста n лет  , то будет произведено
, то будет произведено  выплат величиной
выплат величиной  у.е. каждая.
у.е. каждая. . (17)
. (17)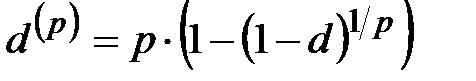 - номинальная ставка дисконтирования, обращаемая с частотой
- номинальная ставка дисконтирования, обращаемая с частотой  - номинальная процентная ставка.
- номинальная процентная ставка. , получим аналогичную формулу и для полной пожизненной ренты:
, получим аналогичную формулу и для полной пожизненной ренты: . (18)
. (18)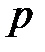 ,
,  . За малый промежуток времени
. За малый промежуток времени  поступит сумма
поступит сумма  . Тогда приведенную стоимость полной непрерывной пожизненной ренты в момент времени
. Тогда приведенную стоимость полной непрерывной пожизненной ренты в момент времени  можем вычислить как
можем вычислить как .
. , можем написать:
, можем написать: .
. . (19)
. (19)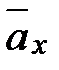 выразить и через упрощающие функции
выразить и через упрощающие функции . (20)
. (20) . Тогда приведенная стоимость такой ренты будет равна
. Тогда приведенная стоимость такой ренты будет равна , (21)
, (21) . (22)
. (22) - искомая нетто-премия. Тогда современная актуарная стоимость обязательств застрахованного
- искомая нетто-премия. Тогда современная актуарная стоимость обязательств застрахованного  будет функцией
будет функцией  , то есть
, то есть  . Актуарная современная стоимость финансовых обязательств компании
. Актуарная современная стоимость финансовых обязательств компании 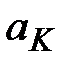 также является функцией
также является функцией  :
:  . И для вычисления
. И для вычисления  необходимо применить принцип финансовой эквивалентности обязательств страховой компании и застрахованного, а это означает, что необходимо решить уравнение:
необходимо применить принцип финансовой эквивалентности обязательств страховой компании и застрахованного, а это означает, что необходимо решить уравнение: , (1)
, (1)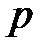 состоит из нескольких частей: периодическая нетто-премия
состоит из нескольких частей: периодическая нетто-премия  и расходы, возмещающие организационные затраты.
и расходы, возмещающие организационные затраты. (4)
(4) новорожденных.
новорожденных. (или
(или  ) называют кривой смертей.
) называют кривой смертей. .
. ,
, .
. и плотность распределения вероятностей
и плотность распределения вероятностей  может быть использована в качестве первичной характеристики продолжительности жизни, так как с помощью
может быть использована в качестве первичной характеристики продолжительности жизни, так как с помощью  можно вычислить функцию выживания
можно вычислить функцию выживания  .
. человека, дожившего до x лет:
человека, дожившего до x лет: . (5)
. (5)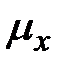 , является величина
, является величина ,
,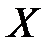 определяют и такие числовые характеристики как математическое ожидание
определяют и такие числовые характеристики как математическое ожидание 
 и дисперсия
и дисперсия  , которые можно вычислить по формулам:
, которые можно вычислить по формулам: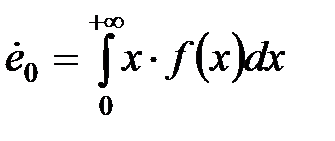 ,
, .
.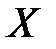 страховщики должны располагать показателями, которые позволяют им оценить риск смерти или дожития до определенного срока для лиц различного пола и возраста. Основной источник - таблицы смертности, которые составляются в каждой стране с определенной периодичностью на основе информации, собираемой в результате переписи населения.
страховщики должны располагать показателями, которые позволяют им оценить риск смерти или дожития до определенного срока для лиц различного пола и возраста. Основной источник - таблицы смертности, которые составляются в каждой стране с определенной периодичностью на основе информации, собираемой в результате переписи населения. - среднее число живых представителей некоторой группы из
- среднее число живых представителей некоторой группы из  новорожденных к возрасту x лет;
новорожденных к возрасту x лет;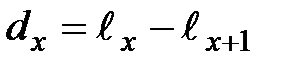 - число представителей группы, умерших в возрасте от x до
- число представителей группы, умерших в возрасте от x до  лет;
лет; - доля тех представителей группы, доживших до возраста x лет, которые умрут в течение ближайшего года;
- доля тех представителей группы, доживших до возраста x лет, которые умрут в течение ближайшего года; - среднее суммарное число лет, прожитых представителями группы в возрасте от x до
- среднее суммарное число лет, прожитых представителями группы в возрасте от x до 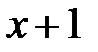 лет;
лет; - среднее суммарное число лет, прожитых представителями группы в возрасте от x лет и более;
- среднее суммарное число лет, прожитых представителями группы в возрасте от x лет и более; - среднее остаточное время жизни.
- среднее остаточное время жизни. для людей и предположил, что X подчиняется равномерному закону распределения вероятностей в интервале
для людей и предположил, что X подчиняется равномерному закону распределения вероятностей в интервале 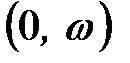 :
: ,
, . (6)
. (6)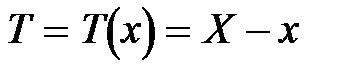 , (7)
, (7)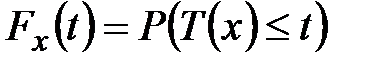 . В страховой математике обозначают как
. В страховой математике обозначают как  :
: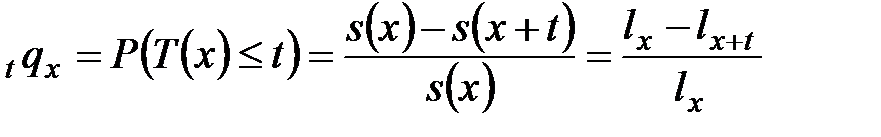 - (8)
- (8) обозначается как
обозначается как  :
: -
- лет.
лет. индекс
индекс  опускают:
опускают:




