Поиск решения и подбор параметров

Для анализа данных в состав Microsoft Excel встроены такие средства как Подбор параметров и Поиск решения. Подбор параметров предназначен для нахождения по известному значению функции y=f(x) неизвестного значения величины х. Поиск решения позволяет среди всех возможных допустимых решений найти оптимальное решение при заданных ограничениях. Рассмотрим использование данных средств на примерах.

 

Поиск решения

Поиск управленческого решения зачастую бывает связан с решением оптимизационных задач, которые имеют следующие основные особенности:

- задана целевая функция, которую требуется максимизировать или минимизировать, или приравнять результат к конкретному значению;

- на неизвестные наложены ограничения в форме неравенств или уравнений;

- ряд неизвестных должен быть неотрицателен.

Большой класс оптимизационных задач составляют задачи, математической моделью которых является модель линейного программирования. В таких моделях целевая функция является линейной функцией и ограничения заданы в виде линейных неравенств и уравнений. В Excel есть мощное средство решения оптимизационных задач, в частности задач линейного программирования - Поиск решения. Рассмотрим две типичные задачи такого рода.

Задача 1:

В таблице приведены данные о предприятии, производящем продукцию двух видов Р₁ и Р₂ из сырья трех видов S₁, S₂, S₃. Запасы сырья равны соответственно b₁, b₂, b₃. Расход i-го вида сырья S₁ на единицу j-го вида продукции Р_j равен a_ij. Доход, получаемый предприятием от реализации единицы j-го вида продукции Р_j равен с_j.

Sj	bi	P1	P2
S1	b1= 70	a11=1	a12=7
S2	b2=54	a21=3	a22=2
S3	b3=41	a31=2	a32=3
	cj

Найти план производства, обеспечивающий предприятию максимум дохода с помощью средства Поиск решения.

Решение данной задачи целесообразно выполнить в три этапа.

Первый этап: Сформулируйте экономико-математическую модель задачи (определите неизвестные, целевую функцию, ограничения на неизвестные). Для этого выполните следующие действия:

· В предлагаемом примере неизвестные величины х₁ и х₂.обозначают соответственно планируемое количество продукции первого вида Р₁ и планируемое количество продукции второго вида Р₂, которые должны обеспечить предприятию максимальный доход. Эти величины должны быть неотрицательны.

· Целевая функция (линейная форма) представляет суммарный доход предприятия от реализации продукции и равна

z=3x₁+7x₂ (1).

· Расход сырья вида S₁, S₂, и S₃ на производство продукции ограничен его запасами b₁, b₂, b₃. Таким образом, возникают ограничения:

1x₁+7x₂≤70;

3x₁+2x₂≤54; (2)

2x₁+3x₂≤41.

В результате приходим к математической формулировке задачи: среди неотрицательных решений системы линейных неравенств (2) найти решение, дающее максимум целевой функции z (1).

Второй этап: Введите исходные данные сформулированной модели на рабочий листследующим образом (рис.7.1):

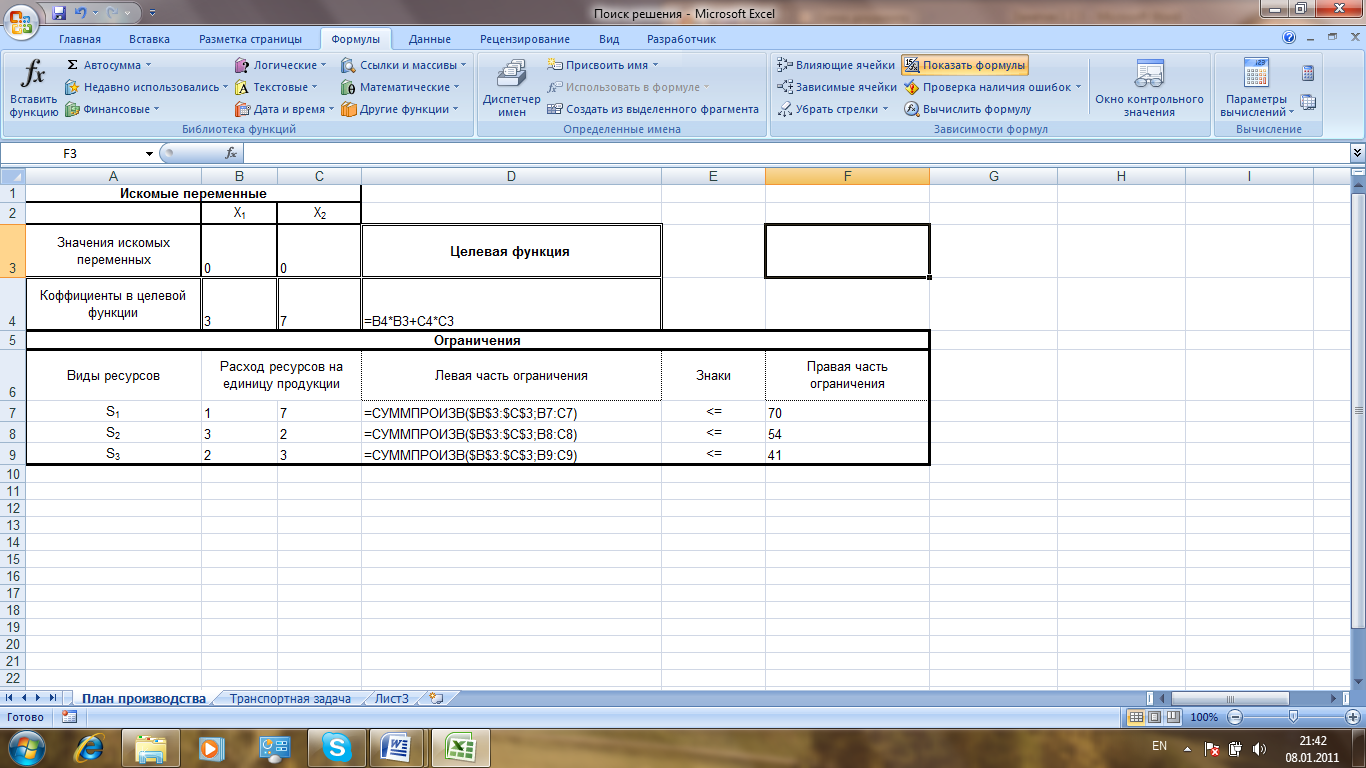
Рисунок 7.1.. Информационная среда для решения задачи линейного программирования

Сначала введите заголовки для всех исходных данных, участвующих в задании модели.

- В ячейку B1 введите заголовок Искомые переменные.

- В ячейки В2 и С2 введите соответственно обозначения для количества производимой продукции первого и второго вида х₁ и х₂ (мы помним, что это неизвестные величины, значения которых при заданных условиях хотим найти).

- В ячейку А3 введите текст Значения искомых переменных.

- В ячейку А4 введите текст Коэффициенты в целевой функции.

- В ячейке D3 введите текст Целевая функция.

- В ячейку А5 введите текст Ограничения.

- В ячейку А6 введите текст Виды ресурсов.

- В ячейки А7, А8, А9 соответственно введите названия вида сырья S₁, S₂, и S_{3 .}

Отформатируйте таблицу так, как показано на рис.1.

Таким образом, в этой модели диапазон ячеек B3:C3 будет содержать оптимальное количество продукции вида Р₁ и вида Р₂. В качестве начальных значений принимаются нули. После применения Поиска решения в них будет помещен результат решения задачи. Ячейки B3 и C3 называются изменяемыми ячейками, т.к. значения в них будут изменяться в ходе решения для того, чтобы максимизировать результат в оптимизируемой (целевой) ячейке D4. Поиск решения позволяет задавать до 200 изменяемых ячеек. Изменяемые ячейки не должны содержать формул и их изменение влияет на результат в оптимизируемой ячейке.

Диапазон ячеек B4:C4 должен содержать стоимость единицы продукции первого и второго вида, в терминах математической модели – это коэффициенты в целевой функции.

D4 – оптимизируемая ячейка должна содержать формулу, определяющую суммарный доход предприятия от продажи произведенной продукции.

Диапазон ячеек B7:C9 должен содержать количество сырья вида S₁, S₂, и S₃ используемого на единицу выпускаемой продукции вида Р₁ и вида Р₂.

В диапазоне ячеек D7:D9 вычисляется объем используемого сырья. Очевидно, что количество использованного сырья не может превышать количество имеющегося на складе. Количество сырья на складе содержится в диапазоне ячеек F7:F9.

Введите в созданную форму остальной текст и исходные данные (см. рис.7. 1), а затем добавьте формулы:

1. В ячейку D4 введите формулу =B4*B3+C4*C3, определяющую суммарный доход предприятия от реализации продукции. Поскольку доход нужно максимизировать, то ячейку D4 назовем оптимизируемой или целевой ячейкой.

2. В ячейку D7 введем формулу, вычисляющую количество сырья вида S₁, необходимого для производства продуктов вида Р₁ и вида Р₂. Эта формула представляет собой сумму произведений значений ячеек диапазона B3:C3 на соответствующие значения ячеек из диапазона B7:В9. Формулу можно записать самим, а можно воспользоваться функцией СУММПРОИЗВ. В случае использования функции выполните следующие действия:

a. Активизируйте ячейку D7.

b. Вызовите Мастер функций, нажав в строке формул кнопку f_x.

c. В появившемся диалоговом окне Мастер функций шаг 1 из 2 в окне Категория выделите Математические, а в окне Выберите Функцию щелкните мышью по СУММПРОИЗВ и нажмите на кнопку ОК.

d. Во втором диалоговом окне установите курсор ввода символов в поле ввода Массив 1. Затем протащите мышь при нажатой левой кнопке мыши по ячейкам B3:C3, предварительно отодвинув активное диалоговое окно с этих ячеек.

e. Установите курсор ввода символов в поле ввода Массив 2. Затем протащите мышь при нажатой левой кнопке мыши по ячейкам B7:C7, предварительно отодвинув активное диалоговое окно с этих ячеек, и нажмите на кнопку ОК или клавишу Enter. Таким образом, функция введена в ячейку D7 и имеет вид =СУММПРОИЗВ(B3:C3; B7:C7).

f. Аналогичные функции должны быть введены в ячейки D8 и D9. Они отличаются от введенной в D7 функции диапазоном ячеек второго массива, а первый массив во всех трех случаях одинаков. Поэтому выполним копирование введенной функции с помощью маркера автозаполнения в ячейки D8, D9, но предварительно в параметрах функции сделайте абсолютными имена ячеек B3 и C3. Для этого выделите ячейку D7 и установите курсор ввода символов в строку формул сначала перед буквой В и нажмите на клавиатуре функциональную клавишу F4, а затем установите курсор ввода символов перед буквой С и снова нажмите на клавиатуре функциональную клавишу F4, а затем Enter. Формула должна иметь вид, как на рис. 7.1.

На этом ввод ограничений и формул закончен. Обратите внимание на то, что в таблице на рис.7.1 выбран режим отображения формул, то есть нажата кнопка Показать формулы, и введенные формулы видны в ячейках. В обычном режиме в ячейках отображаются результаты, полученные после расчета формул, а сами формулы можно увидеть только в строке формул.

Третий этап: Этот шаг связан с поиском наилучшего решения и требует выполнения следующих действий:

- Сохраните построенную модель на жестком диске при помощи команды Office, Сохранить как в своей папке под именем Планирование производства.

- Выделите оптимизируемую ячейку D4.

- Выполните команду Данные, Анализ, Поиск решения [1]. После этого появится диалоговое окно Поиск решения (рис. 2).

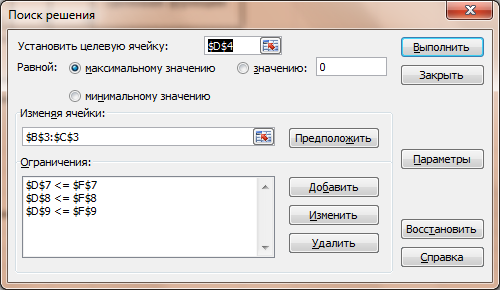
- В поле Установить целевую ячейку уже находится ссылка на оптимизируемую ячейку, так как она была выделена перед вызовом Поиска решения. При необходимости эту ссылку можно изменить обычным образом. Программа Поиск решения может оптимизировать результат только в одной ячейке. Напомним, что в целевой ячейке должна находиться формула, которая содержит ссылки на изменяемые ячейки рабочего листа.

- Выберите тип взаимосвязи между целевой ячейкой и решением путем выбора переключателя в группе Равной – Максимальному значению. В этом случае отыскивается максимальный результат для целевой ячейки.

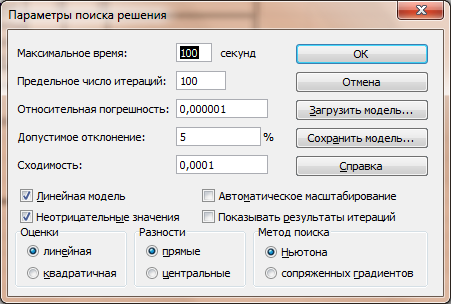
Рисунок 7.2. Диалоговое окно Поиска решения

- Перейдите в поле Изменяя ячейки и укажите смежные ячейки B3:C3, которые должны изменяться в процессе поиска наилучшего решения. Для этого протащите мышь при нажатой левой кнопке мыши по ячейкам B3:C3.

- Введите ограничения, нажав на кнопку Добавить. Откроется диалоговое окно Добавление ограничения.

- Введите первое ограничение. Для этого установите курсор ввода символов в поле Ссылка на ячейку и щелкните левой кнопкой мыши по ячейке D7. Справа от поля Ссылка на ячейку в раскрывающемся списке, выберите знак отношения между левой и правой частью введенного ограничения. В нашем случае – это знак ≤. Установите курсор ввода в поле Ограничение и щелкните левой кнопкой мыши по ячейке F7.

- Нажмите кнопку Добавить, чтобы ввести следующее ограничение.

- Ввести остальные ограничения.

- После ввода последнего ограничения в диалоговом окне Добавление ограничения нажмите на кнопку Ок. Появится заполненное диалоговое окно Поиск решения.

- Введите дополнительные параметры для решения задачи линейного программирования (рис. 3):

a. Откройте окно Параметры поиска решения, нажав кнопку Параметры в окне Поиск решения.

b. Установите флажок Линейная модель.

c. Установите флажок Неотрицательные значения.

d. Нажмите кнопку Ок. Вновь появится заполненное окно Поиск решения.

- Нажмите кнопку Выполнить. По окончании поиска решения появится диалоговое окно Результаты поиска решения. С его помощью можно сформировать отчет.

 

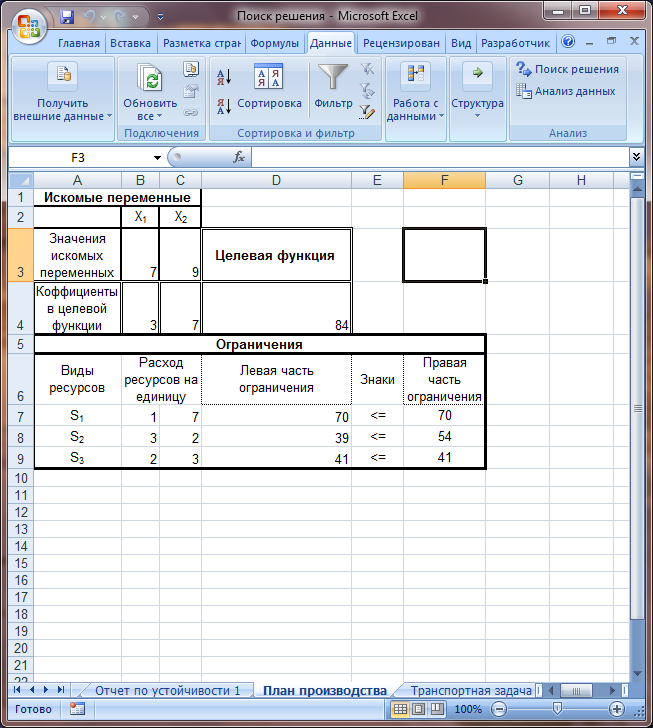
Рисунок 7.3. Диалоговое окно Параметры поиска решения

- Выберите переключатель Сохранить найденное реш ение и нажмите кнопку ОК.

- Таблица с окончательным решением представлена на рис. 7.4. Самостоятельно проанализируйте полученные результаты и сделайте выводы.

-

 

Рисунок 7.4. Решение задачи планирования производства.

Задача 2.

Рассмотрим решение еще одной задачи линейного программирования, которую также можно решать с помощью механизма Поиск решения, – транспортной задачи. Исходные данные транспортной задачи заданы таблицей, в которой:

- В первом столбце указано, сколько единиц груза может доставить поставщик;

- В первой строке указано, сколько единиц груза хочет получить потребитель;

- В остальных ячейках таблицы указаны удельные транспортные затраты на перевозку единицы груза.

bj ai

 

 

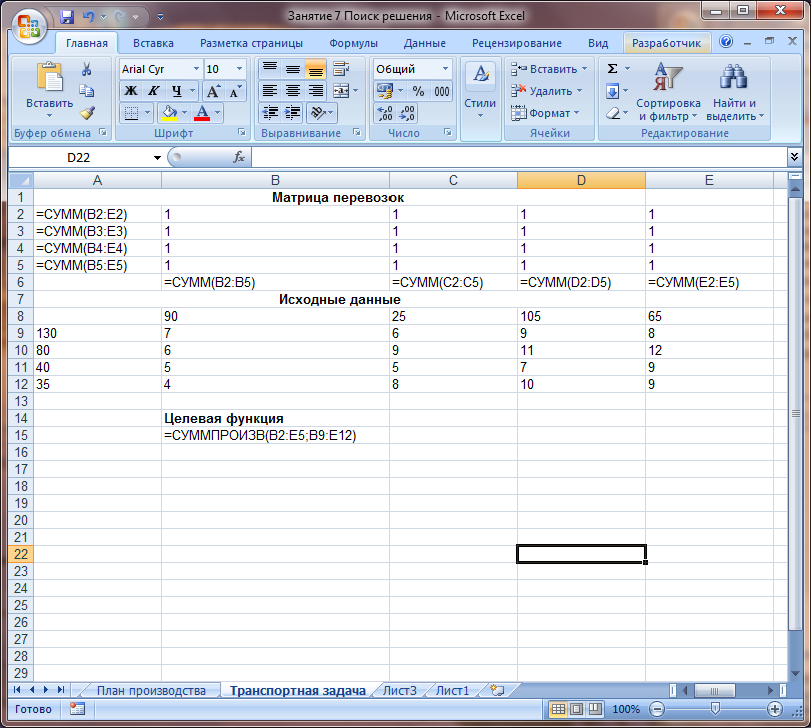
Используя средство Поиск решения, найти оптимальный план перевозок, минимизирующий стоимость перевозок при условии, что все поставщики вывезут груз, а все потребители его получат в полном объеме.

Этапы решения задачи:

Первый этап: Сформулируйте экономико-математическую модель задачи (определите неизвестные, целевую функцию, ограничения на неизвестные).

- В предлагаемом примере 16 неизвестных величин х₁₁, х₁₂, х₁₃, х₁₄, х₂₁, х₂₂, х₂₃, х₂₄, х₃₁, х₃₂, х₃₃, х₃₄, х₄₁, х₄₂, х₄₃, х₄₄,обозначают количество единиц груза, перевезенных от i-го поставщика j-му потребителю, где i, j изменяются от 1 до 4. Эти величины должны быть неотрицательны.

- Целевая функция (линейная форма) представляет суммарную стоимость перевозок, которую следует минимизировать:

z=7х₁₁+6х₁₂+9х₁₃+8х₁₄+6х₂₁+9х₂₂+11х₂₃+12х₂₄+
5х₃₁+5х₃₂+7х₃₃+9х₃₄+4х₄₁+8х₄₂+10х₄₃+9х₄₄ (1).

- Все грузы должны быть перевезены, все потребности должны быть удовлетворены. Таким образом, возникают ограничения (2):

х₁₁+ х₁₂+ х₁₃+ х₁₄=130;

х₂₁+ х₂₂ +х₂₃ +х₂₄=80; (2)

х₃₁+ х₃₂ +х₃₃ +х₃₄=40;

х₄₁ +х₄₂ +х₄₃ +х₄₄=35;

х₁₁+х₂₁+х₃₁+х₄₁=90;

х₁₂+ х₂₂ +х₃₂ +х₄₂=25;

х₁₃+ х₂₃ +х₃₃ +х₄₃ =105;

х₁₄+х₂₄ +х₃₄ +х₄₄=65.

В результате приходим к математической формулировке задачи: среди неотрицательных решений системы линейных уравнений (2) найти решение, дающее минимум целевой функции z (1).

Второй этап: Введите исходные данные сформулированной модели на рабочий лист следующим образом:

- Сначала введите заголовки для всех исходных данных, участвующих в определении модели (рис.7.5.).

- Введите исходные данные – коэффициенты при неизвестных в целевой функции в диапазон ячеек B9:E12, количество груза у поставщиков в ячейки A9:A12 и потребности в грузе у потребителей в ячейки B8:E8.

- Для формирования левых частей уравнений (2), являющихся ограничениями, введите формулы в ячейки А2:А5 и в ячейки В6:Е6, как показано на рис.7.5.

- В ячейку В15 введите целевую функцию.

Таким образом, в этой модели диапазон ячеек B2:Е5 будет содержать оптимальный план перевозок x_ij. В качестве начальных значений, для того чтобы изменяемые ячейки были видны, возьмем единицы. После применения Поиска решения в них будет помещен результат решения задачи. Ячейки B2:Е5 называются изменяемыми ячейками, т.к. значения в них будут изменяться в ходе решения для того, чтобы минимизировать результат в оптимизируемой (целевой) ячейке В15.

 

Рисунок 7.5. Электронная таблица для решения транспортной задачи

Диапазон ячеек B9:Е12 содержит стоимости перевозок единицы груза от отправителя i к потребителю j, в терминах математической модели – это коэффициенты в линейной форме.

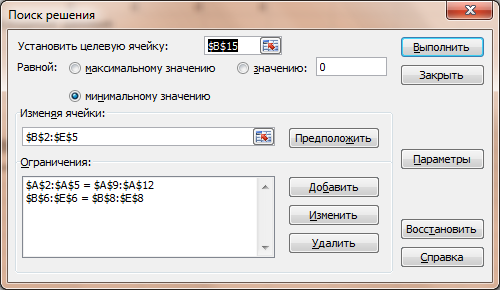
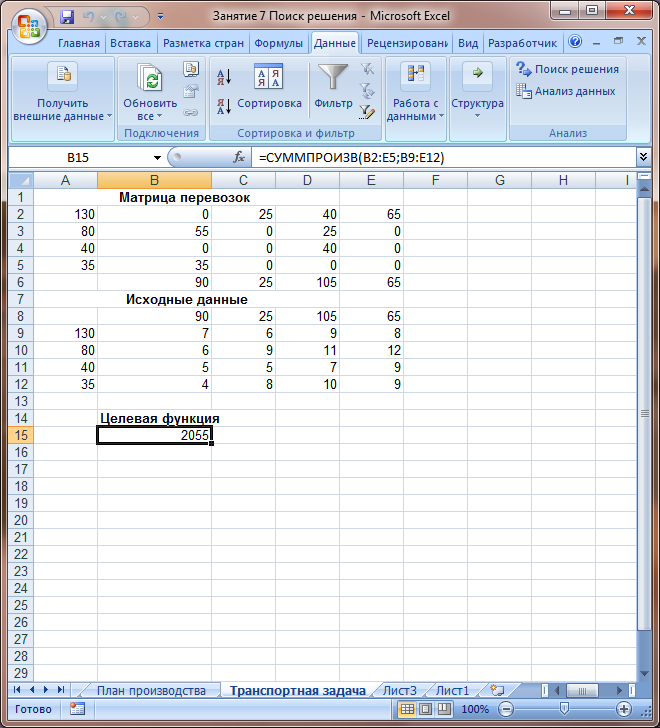
В15 – оптимизируемая ячейка содержит формулу, определяющую суммарную стоимость перевозок.

Диапазон ячеек А9:А12 содержит количество груза, отправляемого поставщиками.

Диапазон ячеек В8:Е8 содержит количество груза, которое хотят принять потребители.

В диапазоне ячеек А2:А5 вычисляются суммы поставок отправителей. Очевидно, что суммарное количество отправленного груза для каждого поставщика из условий задачи в точности должно быть равно имеющемуся количеству груза каждого поставщика. Количество груза содержится в диапазоне ячеек А9:А12.

В диапазоне ячеек В6:Е6 вычисляется суммарное количество груза, поставляемое каждому потребителю. Очевидно, что суммарное количество полученного груза для каждого потребителя из условий задачи в точности равно заказу потребителя. Количество груза, требующееся каждому потребителю, содержится в диапазоне ячеек В8:Е8.

Третий этап: Этот шаг связан с поиском наилучшего решения и требует выполнения следующих действий:

1.Сохраните построенную модель на жестком диске при помощи команды Office, Сохранить как в своей папке под именем Транспортная задача.

2.Выделите оптимизируемую ячейку В15.

3.Выполните команду Данные, Анализ, Поиск решения. После этого появится диалоговое окно Поиск решения.

4.В поле Установить целевую ячейку уже находится ссылка на оптимизируемую ячейку, так как она была выделена перед вызовом Поиска решения.

5.Выберите тип взаимосвязи между целевой ячейкой и решением путем выбора переключателя в группе Равной – Минимальному значению.

6.Перейдите в поле Изменяя ячейки и укажите смежные ячейки В2:Е5, которые должны изменяться в процессе поиска наилучшего решения. Для этого протащите мышь при нажатой левой кнопке мыши по этим ячейкам.

7.Введите ограничения, нажав на кнопку Добавить. Откроется диалоговое окно Добавление ограничения.

8.Введите первое ограничение. Для этого установите курсор ввода символов в поле Ссылка на ячейку и протащите мышь по ячейкам А2:А5.

9.Справа от поля Ссылка на ячейку в раскрывающемся списке, выберите знак отношения между левой и правой частью введенного ограничения. В нашем случае – это операция =.

10. Установите курсор ввода символов в поле Ограничение и протащите мышь по ячейкам А9:А12.

11. Нажмите кнопку Добавить, чтобы ввести следующее ограничение.

12. После ввода второго ограничения (В6:Е6 = В8:Е8) в диалоговом окне Добавление ограничения нажмите на кнопку Ок. Появится заполненное диалоговое окно Поиск решения.

13. Введите дополнительные параметры для решения задачи линейного программирования:

a. Откройте окно Параметры поиска решения.

b. Установите флажок Линейная модель.

c. Установите флажок Неотрицательные значения.

d. Нажмите кнопку Ок. Вновь появится заполненное окно Поиск решения.

14. Нажмите кнопку Выполнить. По окончании поиска решения появится диалоговое окно Результаты поиска решения. С его помощью можно сформировать отчет.

15. Выберите переключатель Сохранить найденное решение и нажмите кнопку ОК. Проанализируйте полученные результаты и сделайте выводы.