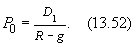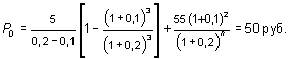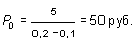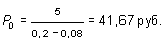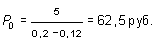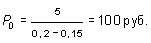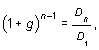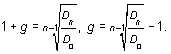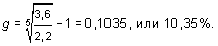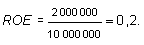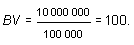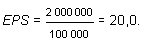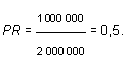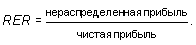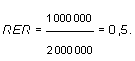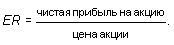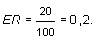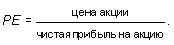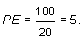Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
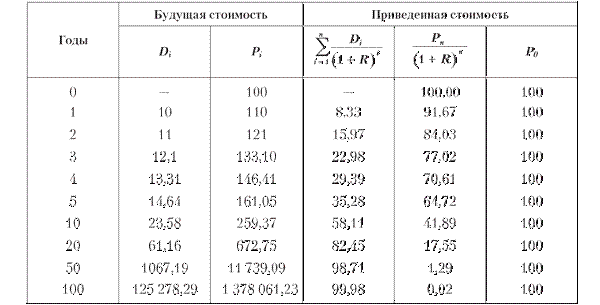
Будущая и приведенная стоимости дивидендов и цены акций «Танис», руб.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Данные таблицы свидетельствуют о том, что с течением времени доля цены в приведенной стоимости акции постепенно уменьшается и уже к десятому году составляет менее 50%; к сотому году приведенная стоимость почти полностью определяется величиной дивидендов. Поскольку акция является бессрочной бумагой, то величина последней составляющей в формуле (13.42) при неограниченном росте n стремится к нулю. Следовательно, текущую цену акции можно представить как приведенную стоимость бесконечного потока дивидендов:
Справедливости ради следует сказать, что практическое использование формулы (13.44) весьма проблематично, так как невозможно определить размер дивидендов на длительный, а тем более бесконечный период времени. Кроме того, многие инвесторы планируют свои действия на ограниченный период времени. Портфель ценных бумаг инвестора постоянно обновляется ¾ для достижения своих целей инвестору необходимо продавать одни ценные бумаги и покупать другие. Таким образом, более реалистичной является ситуация, когда инвестор покупает акции, а через какое-то время их продает. В этом случае расчет цены акции осуществляется по формуле (13.42). Задача инвестора состоит в том, чтобы как можно точнее спрогнозировать величину ожидаемых дивидендов и изменение будущей цены акции. Наиболее простой способ решения проблемы заключается в том, что мы предполагаем постоянные темпы роста цены и дивидендов. Если компания стремится поддерживать постоянный темп роста дивидендов, то можно записать следующее: D2 = D1 ´ (1 + g) D3 = D2 ´ (1 + g) = D1 ´ (1 + g)2, Di = D1 ´ (1 + g)i-1, (13.45) где D 1, D 2, … Di ¾ дивиденды первого, второго, … i -го года; g ¾ темп прироста дивидендов. Подставляя в формулу (13.42) соответствующие значения Di, получаем:
Обозначим:
тогда:
Мы видим, что выражение (13.47) представляет собой сумму первых n членов геометрической прогрессии, которая может быть определена по формуле
Подставляя вместо a 1 и q соответствующие значения, получаем:
Отсюда:
Если рассматривать акцию как бессрочную ценную бумагу, то при неограниченном возрастании числа членов (n ®¥) и при | q | < 1 сумма Sn стремится к пределу:
Подставляя вместо а 1 и q соответствующие значения, имеем:
Ранее было показано, что при неограниченном возрастании числа n (n ®¥) последняя часть в формуле (13.49)
Заметим, что формула (13.52) справедлива при g = сonst и R > g.
Пример 32. На фондовом рынке продаются акции акционерного общества «Ориент». Ожидаемые дивиденды в следующем году ¾ 5 руб. на акцию, а ожидаемая цена акции ¾ 55 руб. Прогнозируемые темпы прироста дивидендов и курсовой цены ¾ 10% в год. Требуемая норма прибыли на акцию ¾ 20% годовых. Определить цену акции, если инвестор собирается держать акцию: а) три года, б) неограниченное время.
Решение. а) Используя формулу (13.49), получаем:
б) Используя формулу (13.52), получаем:
Как видим, применение формул (13.49) и (13.51) приводит к одним и тем же результатам. Иначе и быть не может, так как цена акций должна быть одинакова независимо от того, на какой срок приобретает ее инвестор ¾ на короткое или длительное время. На основании формулы (13.52) нетрудно заключить, что при требуемой норме доходности и ожидаемого уровня дивидендов первого года цена акции будет зависеть от темпа роста дивидендов.
Пример 33. Ожидаемые дивиденды на акцию компании «Ориент» в следующем году прогнозируются в размере 5 руб. Требуемая норма прибыли на акцию составляет 20% годовых. Определить цену акции, если темп прироста дивидендов прогнозируется в размере: а) 8% в год; б) 10% в год; в) 12% в год; г) 15% в год.
Решение. Используя формулу (13.52), получаем: а) б) в) г) Мы видим, что по мере того, как темп прироста дивидендов (g) приближается к требуемой норме прибыли (R), цена акции возрастает. Задача инвестора состоит, следовательно, в том, чтобы правильно определить темп роста дивидендов. Для прогнозирования темпа роста дивидендов можно использовать данные о выплате дивидендов за прошлые годы. Например, известно, что дивиденды на акцию компании «Фарма» составляли: 1995 г. ¾ 2,2 руб., 1996 г. ¾ 2,4 руб., 1997 г. ¾ 2,5 руб., 1998 г. ¾ 3 руб., 1999 г. ¾ 3,1 руб. 2000 г. ¾ 3,6 руб. Если предположить, что темп роста дивидендов является в этом периоде постоянным, то, как было показано ранее, дивиденд любого года можно определить через дивиденд базисного года по формуле (13.45): Dn = D1 ´ (1 + g)n-1,
В нашем примере D 1 = 2,2 руб.; D 6 = 3,6 руб.;
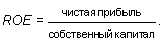
Ожидаемые темпы роста дивидендов можно спрогнозировать также на основе использования данных бухгалтерской отчетности исследуемой компании. Покажем это на конкретном примере. Пример 34. По результатам истекшего года чистая прибыль компании «Вента» составила 2,0 млн долл. На выплату дивидендов было направлено 1 млн долл. Остальная прибыль была направлена на развитие производства. Собственный капитал компании на конец года составляет 10 млн долл. Компанией выпущено и размещено 100 тыс. обыкновенных акций номиналом 75 долл. По имеющимся данным рассчитываем ряд коэффициентов, которые будут нам необходимы для выполнения поставленной задачи. Норма прибыли на собственный капитал, или рентабельность собственного капитала (return on equity):
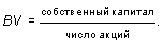
Балансовая стоимость акции (book value per share):
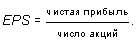
Чистая прибыль на акцию (earnings per share):
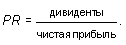
Коэффициент выплаты дивидендов (payout ratio):
Коэффициент реинвестиций (retained earnings ratio):
Ясно, что PR + RER = 1. Коэффициент «прибыль-цена акции» (earnings-price ratio):
Обратный коэффициент «отношение цены акции к доходу» (price-earnings ratio):
Предположим, что «Вента» будет и дальше получать прибыль в размере 20% на собственный капитал и 50% этой прибыли инвестировать. Это значит, что балансовая стоимость собственного капитала компании увеличится на следующий год на 10% (0,2 ´ 0,5). Если предположить, что рентабельность собственного капитала и коэффициент дивидендных выплат останутся неизменными (т. е. 20% и 50%), то прибыль и дивиденды в расчете на акцию также увеличатся на 10%, т. е. темп прироста дивидендов составит: g = ROE ´ RER = 0,2 ´ 0,5 = 0,1, или 10%. Таким образом, основываясь на результатах работы компании «Вента», можно предположить, что темпы прироста дивидендов составят 10% в год. Посмотрим, какие результаты будет иметь компания «Вента», если ожидаемые темпы прироста дивидендов и рассчитанные выше показатели останутся неизменными в течение ближайших пяти лет (табл. 13.4). Таблица 13.4
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 4243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.132.147 (0.012 с.) |

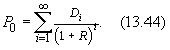
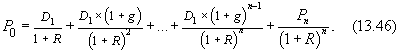
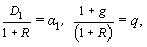
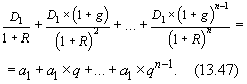
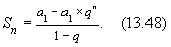
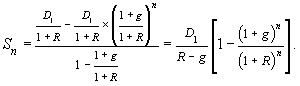
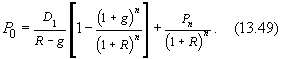
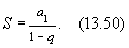
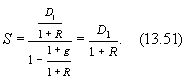
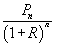 стремится к нулю. Следовательно:
стремится к нулю. Следовательно: