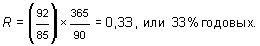Доходность за период владения

Инвестор может держать облигацию не до погашения, а продать ее до срока погашения. В этом случае требуется определить доходность за период владения. Расчет доходности облигаций при этом фактически не отличается от методов расчета доходности к погашению. Разница лишь в том, что инвестор получает не сумму погашения (номинальная облигация), а продажную цену облигации, которая может отличаться от номинала. Поэтому в приведенных выше формулах вместо номинала облигации будет фигурировать цена продажи облигации.

 

Пример 15.

Инвестор приобрел бескупонную облигацию номиналом 1000 руб. за 600 руб. и продал ее через 2 года за 800 руб. Определить доходность за период владения.

Используя формулу (13.18), получаем:

 

Пример 16.

Государственная краткосрочная облигация номиналом 100 руб. была куплена инвестором за 85 руб. и продана через 90 дней за 92 руб. Определить доходность за период владения.

Используя формулу (13.21), имеем:

 

Пример 17.

Инвестор приобрел облигацию номиналом 1000 руб. за 930 руб. Через 2 года он продал облигацию за 950 руб. За время владения облигацией он получал процентный доход в размере 200 руб. за каждый год. Определить доходность облигации.

Для решения задачи можно использовать метод последовательных приближений. Однако неплохие результаты, как отмечалось выше, дает формула для нахождения приблизительного уровня доходности. Используя формулу (13.17), получаем:

 

Реализованный процент

Предположим, что инвестор определил для облигации величину доходности к погашению. Он считает, что этот уровень доходности является приемлемым, и инвестор решил оставить облигацию у себя до погашения. В таком случае задача инвестора заключается не только в том, чтобы получать купонные платежи, но и реинвестировать полученные суммы, чтобы обеспечить теоретически определенный уровень доходности.

 

Пример 18.

Облигация номиналом 1000 руб. погашается через 5 лет. Ставка купона ¾ 15% годовых, выплата процентов один раз в год. Инвестор приобрел облигацию за 800 руб. Инвестор рассчитывает, что сможет реинвестировать процентные доходы под 20% годовых. Спрашивается, какую сумму будет иметь инвестор после погашения облигации?

Доходы инвестора от владения облигацией будут складываться от ежегодных процентных платежей и основной суммы (номинала) облигации при ее погашении.

Если бы инвестор не реинвестировал процентные доходы, то при погашении облигации он имел бы 1750 руб. (150 + 150 + 150 + 150 + 1150). Доходность облигации составила бы формула (13.18):

Однако инвестор реинвестирует доходы. Получив 150 руб. в конце первого года, владелец облигации инвестирует эту сумму (например, кладет ее в банк) из расчета 20% годовых сроком на четыре года.

Применяя формулу будущей стоимости (13.1), получаем, что через четыре года (к моменту погашения облигации) эта сумма возрастает до:

150(1 + 0,2)⁴ = 311,04 руб.

Сумма, полученная в конце второго года и инвестированная на срок 3 года, составит:

150(1 + 0,2)³ = 259,2 руб.

Выплата третьего года возрастает до:

150(1 + 0,2)² = 216 руб.

Соответственно, выплата четвертого года будет равна:

150(1 + 0,2) = 180 руб.

В конце пятого года владелец получит 1150 руб. (номинальная облигация и процентный доход). Следовательно, он будет иметь на руках сумму:

311,04 + 259,2 + 216 + 180 + 1150 = 2116,24 руб.

Таким образом, доходность облигации при условии реинвестирования получаемых доходов составит:

Доходность, полученная с учетом реинвестирования доходов (или получения процента на процент), обычно называется как полностью наращенная или капитализируемая ставка доходности. Эту величину называют также реализованным процентом, ставкой рыночной капитализации или ожидаемой нормой прибыли.

Наглядное представление о том, какова разница в уровне доходности, которая достигается при условии реинвестирования получаемых доходов или без реинвестирования, дает график на рис. 13.5.

Рис. 13.5. График доходности облигаций

Величина реализованного процента имеет существенное значение для любого инвестора. Особенно она важна для инвестиционных программ, которые имеют большую величину текущего дохода, когда инвестор должен сам заниматься реинвестированием этих доходов.

Заметим, что приведенный выше метод вычисления реализованного процента дает возможность определить цену облигации. Мы установили, что владелец облигации к концу пятого года будет иметь на руках 2116,24 руб. Спрашивается, какую сумму нужно инвестировать сегодня (например, положить в банк) под 20% годовых, чтобы через пять лет получить 2116,24 руб.? Применяя формулу (2), имеем:

Мы получили тот же самый результат, что и раньше, в примере 1, когда применяли метод дисконтирования доходов.

 

1. Производные ценные бумаги и их характеристика: конвертируемые акции и облигации, варранты, депозитарные расписки.

Производные ценные бумаги - это бездокументарная форма выражения имущественного права (обязательства), возникающего в связи с изменением цены лежащего в основе данной ценной бумаги биржевого актива. Упростив это определение, можно было бы сказать, что производная ценная бумага - это ценная бумага на какой-либо ценовой актив: на цены товаров (обычно биржевых товаров: зерна, мяса, нефти, золота и т.п.); на цены основных ценных бумаг (на индексы акций, на облигации); на цены кредитного рынка (процентные ставки); на цены валютного рынка (валютные курсы).2

В настоящее время эти ценные бумаги получили название деривативы, зачастую называемые также «финансовыми пузырями». Главными видами деривативов являются: конвертируемые облигации, варранты, фьючерсы, опционы, депозитарные расписки и др. разновидности. Операции с производными бумагами проводятся во всех развитых странах, как на первичном, так и на вторичном рынках.