Правила построения сетевых графиков, нахождение критического пути

Правила построения сетевых графиков, нахождение критического пути

По сравнению с другими математическими методами исследования операций, метод сетевого (или календарного) планирования проектов относительно молод, но его ярко выраженная практическая направленность обеспечила ему популяр­ность сразу после рождения.

В 1956 году специалисту в области вычислительной техники из фирмы «Дю­пон» М. Уолкеру, совместно с Д. Келли разработал простой и эффективный метод планирования работ. Метод был основан на построении так называемых сетевых графиков и по­лучил название «метод критического пути», сокращенно МКП (англоязычный ва­риант— CriticalPathMethod — СРМ ).

В США был создан метод анализа и оценки программ ( PERT, от ProgrammeEvaluationandReviewTechnique).

Основное различие между методами СРМ и PERT заключалось в том, что в первом из них длительности входящих в проект работ полагались детерминиро­ванными, а во втором рассчитывалась вероятностная оценка длительности работ. Впоследствии оба метода были объединены под общим названием PERT-СРМ (наиболее распространенный русскоязычный вариант — метод сетевого плани­рования и управления).

К настоящему времени технология сетевого планирования и управления уже достаточно хорошо отлажена и отлично зарекомендовала себя в таких областях деятельности, как разработкам подготовка к производству новых видов изделий, строительство и реконструкция, проведение научно-исследовательских и опыт­но-конструкторских работ, и, наконец, разработка программных продуктов.

Этап структурного планирования начинается с разбиения исследуемой операции (программы, проекта) на четко определенные шаги (работы), необходимые для достижения цели операции. Затем определяются оценки продолжительности ра­бот и строится сетевой график. Сетевой график состоит из элементов двух видов — работ и событий, и позво­ляет в наглядной форме представить структуру проекта с точки зрения входящих в него работ. Другими словами, сетевой график отображает взаимосвязи между работами внутри проекта и порядок их выполнения.

С математической точки зрения он является направленным графом, в кото­ром каждая работа представляется ориентированной дугой, а каждое событие — вершиной (узлом). Каждое событие определяется как момент времени, когда завершается одна работа (или группа работ) и начинается другая. Любая работа, включенная в сетевой график, считается описанной (заданной), если указаны номера событий, между которыми она заключена, и ее длительность.

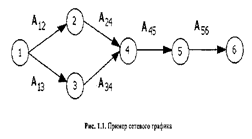
В качестве примера на рис. 1.1 приведен сетевой график, отображающий (в упрощенном виде) структуру работ при создании программного продукта, состоящего из двух относительно самостоятельных модулей.

Изображенные на рисунке дуги соответствуют следующим видам работ:

А₁₂ — разработка алгоритма первого модуля;

А₁₃ — разработка алгоритма второго модуля;

А₂₄ — программирование первого модуля;

А₃₄ — программирование второго модуля;

А₄₅ — комплексная отладка модулей;

А₅₆ — разработка программной документации.

Основные правила построения сетевого графика.

 

1. Каждая работа представляется одной и только одной дугой, то есть ни одна работа не должна появляться в графике дважды. При этом любая работа в случае необходимости может быть разбита на две или более частей, каждой из которых будет соответствовать своя дуга. Например, программирование модуля можно представить как две работы: ввод текста программы и ее от­ладку.

2. Ни одна пара работ не должна определяться одинаковыми начальным и конеч­ным событиями (в противном случае две различные работы будут идентифи­цированы одинаково). Возможность такого неоднозначного задания работ су­ществует в тех случаях, когда две (или более) работы могут выполняться од­новременно.

3. Ни одно событие не может произойти до тех пор, пока не будут закончены все входящие в него работы. Например, комплексная отладка модулей не может быть начата до завершения программирования каждого из них, то есть собы­тие 4 на рис. 1.1 не произойдет до завершения работ А₂₄ и А₃₄.

4. Ни одна работа, выходящая из данного события, не может начинаться до тех пор, пока не произойдет данное событие; например, программирование пер­вого модуля (работа А₂₄) не может начаться, если не закончена разработка его алгоритма (то есть пока не произошло событие 3). Чтобы исключить нео­днозначность, вводят фиктивную работу и фиктивное промежуточное собы­тие. Затраты времени и ресурсов на выполнение фиктивной работы прини­маются равными нулю.

Сетевой график позволяет прежде всего оценить (определить) временные ха­рактеристики проекта и входящих в него работ. В этом отношении наиболее важ­ное значение в построении плана проекта имеют так называемые критические работы .

Работа считается критической, если задержка ее начала приводит к задер­жке срока окончания проекта в целом. Некритическая работа отличается тем, что промежуток времени между ее ранним началом и поздним окончанием больше ее фактической продолжительности. Другими словами, любая некритическая рабо­та имеет резерв времени. Критический путь представляет собой непрерывную последовательность критических работ, связывающую исходное и завершающее события сети (се­тевого графика).

С содержательной точки зрения длительность критического пути определяет минимально возможную продолжительность проекта в целом (то есть для пост­роенного сетевого графика работ быстрее завершить проект не получится). Если вычисленная длительность Критического пути вас не устраивает, необходимо пе­ресмотреть структуру сетевого графика.

Но, Kak было указано выше, для построения критического пути требуется вы­явить все критические работы проекта. Для этого необходимо найти такие рабо­ты, для которых резерв времени равен нулю.