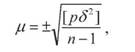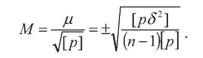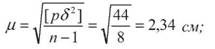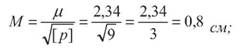Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип арифметичної серединиСодержание книги
Поиск на нашем сайте
Нехай виміряли n разів величину X, то згідно формули (23) можемо записати
Додамо члени рівняння (30), і суму розділимо на їх число n, отримаємо
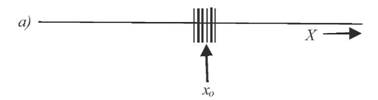
Величина вимірів -C, або просто середнім арифметичним, яке позначимо через Xo Тоді отримаємо Xo-X=JA!. (32) n Згідно формули (28) Тому формула (32) прийме вигляд lim xo = X, n— тобто, проста арифметична середина прямує до її істинного значення при необмеженому зростанні числа вимірів. Пояснити це можна приведеними схемами на рис. 40.
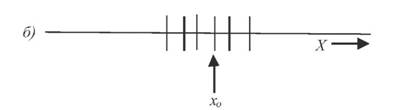
Рис. 40. Результати багаторазових вимірів одної і тої ж величини У випадку, коли величина Xлежить близько до Xo то різниця буде малою (рис 40, а), тоді як у випадку представленому на рис.40, б різниця буде великою. Другими словами, чим більше розсіювання результатів, тим більша повинна бути похибка величини xo. При цьому вважають, що систематичні похибки відсутні. Середня квадратична похибка одного виміру Карл Фрідріх Гаусс запропонував оцінку точності проведених вимірів в геодезії виконувати за формулою:
Дану похибку К.Ф. Гаусс назвав середньоквадратичною. Середня квадратична похибка є надійним критерієм оцінки точності вимірів. Вона має наступні позитивні властивості. На величину середньої квадратичної похибки сильно впливають великі по абсолютній величині похибки, які по суті і визначають якість виконаних вимірів. Це відбувається тому, що кожна похибка підноситься до квадрату, а їх сума значно зростає за рахунок великих по абсолютній величині похибок. Середня квадратична похибка виявляється стійким критерієм оцінки точності вимірів. Формула (34) передбачає, що число похибок п прямує до безконечності. По величині середньої квадратичної похибки можна визначити граничну похибку Лг, яка може бути при даних умовах вимірів. За таким правилом можна визначати граничну похибку, коли похибки вимірів відповідають вище приведеним чотирьом властивостям випадковим похибкам. Інколи для визначення величини граничної похибки використовують формулу
При досить великому числі вимірів п, граничну похибку обчислюють за формулою
Слід зауважити, що формула (35) значно розширює дію граничної похибки. Тому в технічних інструкціях з виконання геодезичних вимірювань в основному встановлюється більш жорсткіший допуск, тобто
В деяких випадках доцільно користуватися відносною середньою квадратичною похибкою. Відносна похибка вимірювання дорівнює відношенню абсолютної похибки до істинного або дійсного значення виміряної величини й виражається в частках одиниці. Так, якщо довжина лінії d виміряна із середньою квадратичною похибкою md, то наглядно точність вимірювань характеризується дробом, тобто
де M - ціле число знаменника. Відносні похибки зручні для порівняння лінійних характеристик кількох результатів. Справді, порівнюючи абсолютні похибки, важко відразу вирішити, в якому з двох вимірювань отримано вірогідніші результати. Визначення похибок функцій виміряних величин На практиці завжди приходиться виконувати оцінку точності не самих виміряних величин, а функцій виміряних величин, наприклад їх суми або різниці, добутку або ділення. Із теорії похибок відомо наступне. 1. Функція добутку виміряної величини на постійне число. F = k х x, (39) де x - результат виміру; k - постійне число. Середня квадратична похибка такого добутку обчислюється за формулою mF = k х mx. (40) [1] Функція суми величин x, y, z,...,ы (в тому числі і алгебраїчних), виміряних незалежно від другої.
тобто похибка суми однаково точних величин зростає пропорційно кореню квадратному із числа виміряних величин. 3. Функція добутку незалежно виміряних величин.
Тоді
На основі формули (45) видно, що для оцінки точності добутку незалежно виміряних величин необхідно сумувати квадрати не абсолютних, а відносних середніх квадратичних похибок вимірювань. Приклад. Необхідно обчислити середню квадратичну похибку площі F прямокутника, сторони якого b і h визначені із середніми квадратичними похибками mb і mh.
F = bxh (46)
Нерівноточні виміри величии Коли величину вимірюють різними приладами з різною точністю або прийомами, то кінцевий результат буде нерівноточним. При обчисленні середнього значення із нерівноточних результатів враховують вагу кожного результату. Вага - це число, яке характеризує точність будь-якого результату по відношенню до інших результатів. Середнє арифметичне із нерівноточних вимірів називають загальною арифметичною серединою або середнім ваговим.
Нехай при вимірюванні лінії отримали п кінцевих результатів. Отримані результати відрізняються між собою тільки числом вимірів. P1 раз і отримали середній (кінцевий) результат dj P2 раз і отримали середній (кінцевий) результат d2 P3 раз і отримали середній (кінцевий) результат d3 рп раз і отримали середній (кінцевий) результат dn Тоді вагове середнє обчислюють за формулою
Приклад. Виміряна одна і та ж лінія три, два і чотири рази. Середні значення довжини лінії отримали наступні: У випадку, коли b = h, mb = mh = m; dj = 234,76; d2 = 234,70; d3 = 234,74. Знайти середнє вагове. В довільній формі призначають d' =234,65, та обчислюють різниці
Встановлено, що вага виміру обернено пропорційна квадрату середньої квадратичної похибки, тобто
Загальна вага арифметичної середини дорівнює сумі ваг окремих груп вимірів, тобто
При оцінці точності нерівноточних вимірів використовують поняття про середню квадратичну похибку вимірювання, вага якого рівна одиниці
де § - відхилення від середнього вагового результату кожної групи вимірів. Наприклад S1 = do- di; S2 = do- d2; S3 = do- d3; і т. д. Середня квадратична похибка середнього вагового обчислюється за формулою
Наприклад, необхідно обчислити середню квадратичну похибку ваги і загальної арифметичної середини за результатами вище приведеного прикладу табл^ Таблиця 3
9 +2 44 1 • Обчислюють середню квадратичну похибку вимірювання
2. Обчислюють середню квадратичну похибку середнього вагового Кінцевий результат середнього вагового d =234,74 ± 0,008 м; o Відносна середня квадратична похибка обчислюється за формулою
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1060; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.106.100 (0.011 с.) |

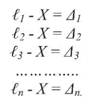 (30)
(30)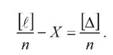 (31)
(31)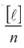 називається середнім арифметичним результатів
називається середнім арифметичним результатів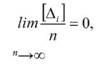
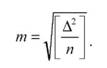
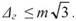
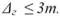
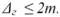
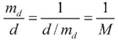
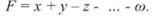
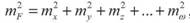
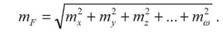
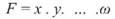
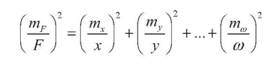

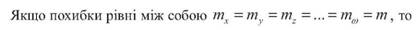
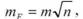
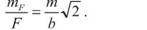
 ' (48)
' (48)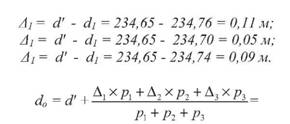
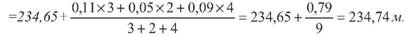
 (49)
(49)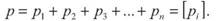 (50)
(50)