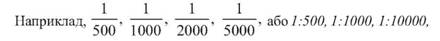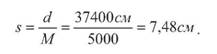Встановлення величини поправки за кривизну Землі

При вивченні фігури Землі встановлено, що вона в наближеному варіанті має геометричну форму сфери. Виникає питання, а яку ділянку рівневої поверхні Землі з необхідною точністю для практичних робіт можна вважати площиною?

Розглянемо частину рівневої поверхні Землі, яка приймається за сферу радіусом R (рис. 7).

На рис. 7 довжина дуги сфери А1 і B1 позначена через s. В точках А1 і B1 проведені радіуси R сфери, які мають продовження до дотичної в точках А і В, АВ = d. Знайдемо, чому дорівнює похибка від заміни дуги s відрізком дотичної d. Різницю між довжиною дотичної d і дугою обчислюють за формулою

Рис.7. Частина сфери

 

 

Оскільки дуга s опирається на центральний кут ф, то

(2)

тоді

(3)

Величину tg—розкладемо в ряд і зупинимося на другому члені, тобто

 

де ф - центральний кут виражений в радіанній мірі, який обчислюється за формулою

 

а тому формула (4) прийме вид

 

Підставляючи (6) в (3), отримаємо

 

Аналізуючи формулу (7) приходимо до висновку, що дотична d довша за дугу s.

Знайдемо відносну похибку різниці Ad за формулою

 

Якщо прийняти R=6371,ll km та надати різні значення s, то можна обчислити величини за формулами (7) і (8). Результати обчислень представимо в табл.1.

Таблиця 1

Результати абсолютних і відносних похибок при заміні дуги s відрізком дотичної d

S, km	Ad, cm	Ad	S, km	Ad,	Ad
s	cm	s
	0,21	1:4 870 000			1:195 000
	1,64	1:1 218 000			1:49 000
	5,55	1:541 000			1:12 200
	13,1	1:30 400			1:5 410

 

Аналізуючи результати табл.1 можна зробити наступні висновки.

Сучасний рівень техніки геодезичних вимірювань довжин ліній 10 - 20 km характеризує найвищу точність відносної похибки, біля 1:1000 000.

Дугу сферичної поверхні Землі довжиною s = 20 km можна замінити дотичною d тому, що відносна похибка різниці дуги і дотичної менша (1:1 218 000) сучасних технічних можливостей вимірювань (1:1 000 000).

3. Ділянку рівневої поверхні Землі діаметром 20 км, або площею 300 - 320 км2, можна прийняти за площину з незначною похибкою, а кривизною поверхні Землі в цих границях можна нехтувати.

Розглянемо вплив кривизни Землі на вертикальне положення точки. На рис. 8 приведений фрагмент сфери, на якій s - дуга сфери, t - дотична в точці А до сфери та Ah похибка впливу кривизни Землі на вертикальне положення точки В.

Розглядаючи рис. 8, на основі теореми Піфагора можна записати

 

звідки

(10)

Якщо замість t підставити s, то величину Ah обчислюють за формулою

(11)

 

Рис. 8. Вплив кривизни Землі на вертикальне положення точки

Враховуючи те, що одиниця значно менша величини 2R, то кінцеве значення Ah можна записати

 

За формулою (12) виконаємо розрахунки, а результати приведемо в табл.2.

Таблиця 2

Вплив кривизни Землі на висоту точки

s, km	Ah, m	s, km	Ah, m	s, km	Ah, m
	0,0785		7,85		196,1981
	1,9619		31,3917		784,7926

 

Аналізуючи табл. 2 можна зробити наступний висновок. Похибкою за вплив кривизни Землі на вертикальне положення точки нехтувати не слід тому, що висоти обчислюють з точністю до

0,1 mm.

Вивчення топографічних карт

Числовий масштаб

Оскільки фігура Землі за своїми розмірами є надто великою, то виготовлення її моделі в натуральну величину неможливо. При виготовленні будь-якої моделі добиваються, щоб вона була подібна оригіналу в зменшеному або в збільшеному (що рідко трапляється) виді і з точністю похибок вимірювання. Щоб цього досягнути необхідно проектувати і будувати модель в горизонтальній проекції. Масштабом називається ступінь зменшення горизонтальних прокладень ліній місцевості при зображені їх на плані або карті. Масштаб записується дробовим числом. В чисельнику обов'язково ставлять одиницю, а в знаменнику число в скільки разів зменшується горизонтальне прокладення ліній на місцевості.

1:25 000. Таким чином, виміряна лінія на місцевості наноситься на план або карту в зменшеному виді відповідно у 500, 1000, 2000, 5000, 10 000 і 25 000 разів. Правдива і наступна інформація. Якщо на плані або карті викреслити відрізок довжиною 1 см, то цьому відрізку на місцевості буде відповідати відрізок 500, 1000, 2000, 5000, 10 000 і 25 000 см.

Основна формула масштабу має наступний вигляд

d = s X M, (13)

де s -кількість сантиметрів на плані або карті; M - знаменник масштабу

Задача 1. На карті масштабу 1:10 000 довжина відрізка s = 2,34 см. Визначити довжину відповідного йому горизонтального прокладання лінії на місцевості d. Згідно формули (13), отримаємо

d = 2,34 см х10 000 = 23400 см =234 м.

Задача 2. Довжина горизонтального прокладення лінії на місцевості d = 374 м. Визначити її довжину на карті масштабу 1:5000. За формулою (13) визначаємо s

 

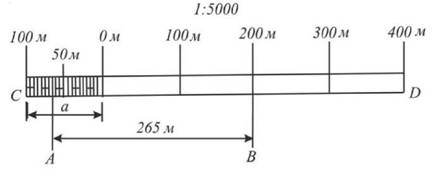
На основі вище приведеного можна зробити наступні висновки.

Чим більший знаменник M числового масштабу, тим масштаб мілкіший.

Чим менший знаменник M числового масштабу, тим масштаб крупніший.

Масштаб 1:50 000 мілкіший масштабу 1:25 000 в два рази, а масштаб 1:2000 крупніший масштабу 1:10 000 в п'ять разів.

Лінійний масштаб

При користуванні числовим масштабом необхідно виконувати певний обсяг обчислювальних робіт, а це при великих об'ємах значно обтяжливо. Тому часто користуються лінійним масштабом. Лінійний масштаб за своєю конструкцією простий у виготовлені та користуванні (рис. 9).

Рис. 9. Лінійний масштаб

 

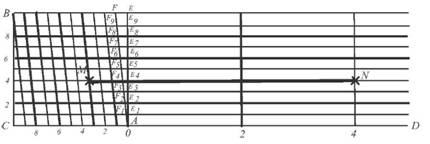
Для побудови на папері лінійного масштабу необхідно накреслити лінію CD, на якій відкласти відрізки однакової довжини, наприклад 2 см. Зліва одне ділення ділять на 10 частин і отримують десяті частини, які в свою чергу дорівнюють 2 мм. Кожних 2 мм поділили на дві частини і отримали величину найменшого ділення рівного 1 мм. Підписують лінійний масштаб згідно прийнятого числового масштабу. Для масштабу 1:5000 в двох сантиметрах на плані або карті буде відповідати на місцевості 100 м, а одне найменше ділення відповідає 5 м. Тому віддаль AB = 265 м. Одне велике ділення а = 2 см називається основою масштабу. Якщо основа відповідає 2 см, то такий масштаб називають нормальним.

Лінійний масштаб за своєю точністю не перевищує 0,5 найменшого ділення масштабу плану. В нашому випадку ця точність буде становити 2,5 м. Як бачимо точність лінійного масштабу відповідно низька, а тому його можна використовувати безпосередньо при рекогностуванні місцевості під час побудови планового і висотного геодезичного обґрунтування, вибору площі для розробки проектів сівозмін, меліоративного осушення та зрошення територій, попереднього вибору осі автомобільної дороги і т. ін.

Поперечний масштаб

Поперечний масштаб є самим точним, а тому його постійно використовують в інженерних розрахунках. Будують лінійку поперечного масштабу наступним чином. На відрізку CD будують декілька основ масштабу а рівних 2 см (рис. 10).

В точках фіксації основ встановлюють перпендикуляри і підписують 0, 2, 4, 6, і 8. Одну основу зліва від підписаного 0 лінійки ділять на 10 рівних поділок і отримують десяті частини основи. Для того, щоб отримати соті частини основи необхідно одну десяту частину поділити на 10 частин. Це досягається тим, що проводять десять ліній паралельних між собою і лінії CD та на однакових відстанях одна від другої. На верхній лінії від

Рис.10. Лінійка поперечного масштабу

 

перпендикуляру з підписом 0 відкладаємо величину відрізка рівного 0,1 частини основи. В нашому випадку таким відрізком буде FE. Точку F сполучають з точкою А і отримують трансверсаль AF. Через нанесені точки ділення на 10 частин відрізків CA і BF проводять паралельні лінії трансверсалі AF. Утворений прямокутний трикутник AEF поділений на 10 частин і кожна така частина є 0,01 вибраної основи. Таким чином відрізки відповідають сотим основі наступні: F1E1 = 0,01 CA; F4E4 = 0,04 CA; F7E7 = 0,07 CA; F2E2 = 0,02 CA; F5E5 = 0,05 CA; FgE8 = 0,08 CA; F3E2 = 0,03 CA; FfE6 = 0,06 CA; F9E9 = 0,09 CA. Для вимірювання віддалей між двома точками на топографічній карті поступають наступним чином. Одну ніжку вимірника ставлять в центр однієї точки, а другу ніжку вимірника ставлять в центр другої точки та не змінюючи розхилу вимірника кладуть його на лінію CD лінійки поперечного масштабу так, щоб одна ніжка співпала з перпендикуляром основи, а друга була обов'язково в районі десятих ділень основи. Пересувають розхил вимірника вверх і паралельно лінії CD так, щоб ніжка вимірника співпала з трансверсалю. Після цього рахують цілі основи, які відділяють комою і після коми записують кількість десятих та сотих. Досвідчені виконавці на око визначають тисячні долі основ.

Наприклад, в нашому випадку між точками M і N на топографічному плані масштабу 1:5000 лінійці поперечного масштабу відповідає 2,34 основ (рис. 10). Оскільки основа має

довжину 2 см, то її на місцевості буде відповідати 100 м. Щоб визначити скільки буде метрів між точками M і N на місцевості необхідно 2,34x100 м = 234 м. Згідно правилу віддаль визначають шляхом множення кількості основ на кількість метрів в одній основі, Таким чином відрізок MN приведений на лінійці поперечного масштабу для планів і карт різних масштабів буде відповідати різним віддалям (рис. 10). Наприклад, для нижче приведених масштабів віддалі, становлять:

1:500 відповідно 10 м x2,34 = 23,4 м;

1:1000 відповідно 20 м x2,34 =46,8 м;

1:2000 відповідно 40 м x2,34 = 93,60 м;

1:5000 відповідно 100 м x2,34 = 234 м;

1:10 000 відповідно 200 м x2,34 = 468 м;

1:25000 відповідно 500 м x2,34 = 1170 м.

Точність масштабу

В геодезичній практиці часто ставлять питання, а з якою точністю виконані виміри? Очевидно точність масштабу це відстань на місцевості яка відповідає довжині відстані найменшого відрізка, який людина може розпізнати на топографічному плані, або карті відповідного масштабу

Відомо, що на плані можна розпізнати неозброєним оком відрізок довжиною 0,1 мм. Такий відрізок відповідає уколу зробленого гострою голкою на аркуші паперу. Тому довжина горизонтального прокладення лінії місцевості, яка відповідає на карті даного масштабу 0,1 мм, називається точністю масштабу. Так, точність масштабів 1:500, 1:1000, 1:2 000 і 1:5 000 дорівнює відповідно 0,05 м, 0,1 м, 0,2 м і 0,5 м.