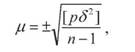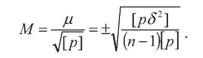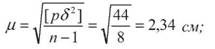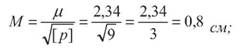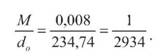Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування проекцій в геодезіїСодержание книги
Поиск на нашем сайте
Геодезія Передмова Вивчення поверхні землі 1.1. Форма і розміри Землі 1.2. Застосування проекцій в геодезії 1.3. План, карта і профіль місцевості за заданим напрямком 1.4. Визначення планового і висотного положення точки на земній поверхні 1.5. Встановлення величини поправки за кривизну Землі Вивчення топографічних карт 2.1. Числовий масштаб 2.2. Лінійний масштаб 2.3. Поперечний масштаб 2.4. Точність масштабу 2.5. Розграфка і номенклатура топографічних карт 2.6. Прямокутна система координат Гаусса-Крюгера Орієнтування 3.1. Вимірювання дирекційних кутів за топографічною картою 3.2. Приклад вимірювання дирекційних кутів за топографічною картою Зображення місцевості на топографічних картах 4.1. Основні форми рельєфу місцевості 4.2. Зображення рельєфу місцевості горизонталями 4.3. Проведення горизонталей за висотами точок 4.4. Крутизна схилу і масштаб закладень 4.5. Обґрунтування висоти перерізу рельєфу 4.6. Розв'язання задач за топографічною картою 4.7. Умовні знаки на топографічних картах Математична обробка результатів вимірювання 5.1. Введення в теорію похибок 5.2. Види похибок вимірювання 5.3. Принцип арифметичної середини 5.4. Середня квадратична похибка одного виміру 5.5. Визначення похибок функцій виміряних величин 5.6. Нерівноточні виміри величии 5.7. Оцінка точності за відхиленнями окремих вимірів Вимірювання довжин ліній 6.1. Компарування сталевої стрічки 6.2. Вимірювання довжин ліній 6.3. Визначення відстаней нитковим віддалеміром 6.4. Вимірювання віддалей світловіддалеміром Будова і перевірки теодолітів 7.1. Будова теодоліта Т30 7.2. Будова теодоліта 2Т30 7.3. Загальні відомості про теодоліти 2Т30 і 2Т30П 7.4. Пристрої для центрування теодолітів 7.6. Перевірки теодоліта Т30 Вимірювання вертикальних і горизонтальних кутів 8.1. Визначення місця нуля (MO) вертикального круга теодоліта та вимірювання кутів нахилу 8.2. Вимірювання магнітного азимута 8.3. Вимірювання горизонтальних кутів способом прийомів 8.4. Вимірювання горизонтальних кутів способом кругових прийомів Будова і перевірки нівелірів 9.1. Будова нівеліра Н-3 9.2. Перевірки і юстування нівеліра Н-3 9.3. Перевірки і юстування нівеліра Н-ЗК з компенсатором 9.4. Перевірки нівелірних рейок
Побудова планових геодезичних мереж методом полігонометрії 10.1. Координатна площина 10.2. Рішення прямої геодезичної задачі 10.3. Рішення оберненої геодезичної задачі 10.4. Схеми побудови теодолітних мереж 10.5. Обчислення координат точок в замкнутому теодолітному ході Побудова планового геодезичного обгрунтування полюсним методом 11.1. Польові роботи при побудові полюсної мережі 11.2. Прив'язка полюсних мереж до вихідних геодезичних пунктів 11.5. Приклад камеральної обробки польових вимірювань полюсної мережі розташованих на ходовій лінії за формулою Побудова висотного геодезичного обгрунтування 12.1. Польові роботи при технічному нівелюванні 12.2. Камеральна обробка результатів технічного нівелювання 12.3. Урівнювання розімкнутого нівелірного ходу технічного нівелювання 12.4. Урівнювання замкнутого полігону Горизонтальне знімання місцевості 13.1. Теодолітне знімання місцевості 13.2. Полярний спосіб 13.3. Спосіб перпендикулярів 13.4. Спосіб кутової засічки 13.5. Спосіб лінійної засічки 13.6. Спосіб створної засічки 13.7. Побудова горизонтального плану Топографічне знімання місцевості методом геометричного нівелювання 14.1. Нівелювання поверхні за квадратами 14.2. Нівелювання поверхні за паралельними лініями 14.3. Нівелювання поверхні за полігонами і створами 14.4. Побудова топографічного плану за результатами нівелювання поверхні Тахеометричне знімання місцевості 15.1. Загальні відомості про тахеометричне знімання 15.2. Основні формули тахеометрії 15.3. Польові роботи при тахеометричному зніманні місцевості 15.4. Побудова топографічного плану за матеріалами тахеометричного знімання Мензульне знімання місцевості 16.1. Суть мензульного знімання 16.2. Основні перевірки кіпрегеля КА-2 16.3. Перевірки кіпрегеля KH 16.4. Підготовка мензули до роботи 16.5. Знімання ситуації і рельєфу Поняття про фотограмметричні знімання місцевості 17.1. Основні відомості про аерофотознімання 17.2. Аерофотознімання місцевості 17.3. Визначення масштабу аерофотознімку 17.4. Поняття про дешифрування 17.5. Трансформування аерофотознімків 17.6. Складання фотопланів 17.7. Обладнання для цифрової фотограмметрії і картографії Геодезичні роботи при перенесені проектів в натуру
18.1. Побудова на місцевості проектного кута 18.2. Побудова на місцевості проектної лінії 18.3. Побудова на місцевості точки з заданою висотою 18.4. Побудова на місцевості лінії і площини заданих ухилів 18.5. Перенесення проектної точки в натуру полярним способом та оцінка його точності 18.6. Перенесення проектної точки в натуру способом перпендикулярів та оцінка його точності 18.7. Перенесення проектної точки в натуру способом кутової засічки та оцінка його точності 18.8. Перенесення проектної точки в натуру способом лінійної засічки та оцінка його точності Камеральні і польові роботи при трасуванні лінійних споруд 19.1. Камеральне трасування осі лінійної споруди 19.2. Польове трасування об'єктів лінійних споруд 19.3. Закріплення основних точок кругової кривої за її віссю 19.4. Розмічування пікетажу по осі лінійної споруди 19.5. Розрахунок пікетажних значень точок кругових кривих 19.6. Детальне розмічування на місцевості кругової кривої 19.7. Спосіб прямокутних координат 19.8. Перенесення пікету на криву 19.9. Спосіб продовження хорд 19.10. Спосіб кутів 19.11. Розмічування поперечників на місцевості 19.12. Заповнення пікетажного журналу в польових умовах 19.13. Технічне нівелювання по осі лінійної споруди 19.14. Камеральна обробка журналу технічного нівелювання 19.15. Побудова поздовжнього і поперечного профілів лінійної споруди 19.16. Проектування за профілем 19.17. Безпікетний спосіб трасування по осі лінійних споруд Загальні відомості з садово-паркового господарства 20.1. Основні задачі садово-паркового господарства 20.2. Розвиток садово-паркового господарства
Геодезія Передмова Книга призначена в якості учбового посібника з геодезії для студентів першого курсу вищих навчальних закладів за напрямом «Лісове і садово-паркове господарство». В книзі висвітленні відомості, вивчення яких дає змогу студенту самостійно виконувати наземні знімання всіх основних видів на невеликій території. Програма курсу «Геодезія» для підготовки студентів вищих навчальних закладів за напрямом «Лісове і садово-паркове господарство» побудована за принципом розглядання окремих видів геодезичних робіт, тобто після викладення попередніх і загальних відомостей, а також питань, пов'язаних із змістом топографічних карт приводяться розділи «Теодолітні роботи», «Нівелірні роботи», «Тахеометричні роботи», «Мензульне знімання місцевості» тощо. Послідовне розкриття різних способів побудови геодезичного обґрунтування і виконання знімань місцевості значно полегшить студентам засвоєння предмету. На сучасному етапі розвитку суспільства геодезичні організації забезпечені новітніми приладами і устаткуванням, які вимагають від виконавця високої фахової підготовки. Методика роботи з новітніми приладами забезпечує високу точність і продуктивність праці. Інноваційні технології внесли значні зміни в технологічний процес інженерно-геодезичних вишукувань. Фахівець садово-паркового господарства повинен володіти традиційними методами геодезичних вимірювань та систематично використовувати новітні геодезичні прилади і технології. В посібнику вдало систематизовані і розглянуті питання загальних відомостей з геодезії, будова та перевірки геодезичних приладів, робота з ними на станції. Широко викладена методика побудови планового і висотного геодезичного обґрунтування. Приведений полюсний метод побудови планового геодезичного обґрунтування, який забезпечує отримання віддалей між точками шляхом обчислення, що значно прискорює визначення прямокутних координат точок мережі. Розглянуто існуючі способи побудови топографічного плану місцевості, виносу проекту в натуру, основи використання аерофотограмметрії при побудові фотосхем та фотопланів.
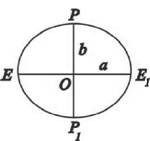
Вивчення поверхні землі Форма і розміри Землі Фізична поверхня Землі є надто складною, тому виразити її математичною формулою неможливо. Вона не відповідає ні одному існуючому фізичному закону. Оскільки людство використовує територію фізичної поверхні для своїх потреб, то виникла необхідність в створенні надійного її обліку. На цій основі виникла ідея підібрати та прийняти форму і розміри типової геометричної фігури, яка є строгою математичною поверхнею і за своєю величиною буде найближчою до існуючої фігури Землі. В подальшому науку спрямували на вивчення елементів відхилень між підібраною типовою геометричною фігурою і існуючою фізичною поверхнею Землі. Прийняту фігуру Землі рахують за рівневу поверхню, твірна якої співпадає з поверхнею води океанів в спокійному стані і уявно продовжена під материками. Така поверхня має властивість, що в кожній її точці прямовисна лінія перпендикулярна до твірної. Вона не співпадає ні з однією поверхнею математичної фігури і сама є неправильною формою, яку називають г е о ї д о м. На основі проведених досліджень встановлено, що математична форма Землі нагадує більше поверхню еліпсоїда, який утворюється від оберту еліпса навколо своєї малої осі (рис.1).
Рис. 1. Земний еліпсоїд Обчисленням півосей а і b еліпсоїда займались багато вчених із різних країн в тому числі і російський вчений Ф.Н. Красовський, який отримав наступні результати: a=6 378 245м; b=6 356 863м; а =(а- b)/a ~ 1/300. Даний еліпсоїд називають референц-еліпсоїдом Красовського. Його поверхня відрізняється від рівневої на величину не більше 150 м. План, карта і профіль місцевості за заданим напрямком Між планом і картою існує вагома різниця. Відомо, що план і карта - зменшене зображення на аркуші паперу горизонтальних проекцій ділянок місцевості. Планом називається зменшене і подібне зображення горизонтальної проекції ділянки місцевості розміром до 20 х 20 км на аркуші паперу. Зображення такої горизонтальної проекції отримане без спотворень, а тому можна сказати, що горизонтальна проекція невеликої ділянки місцевості і її зменшене зображення на аркуші паперу подібні.
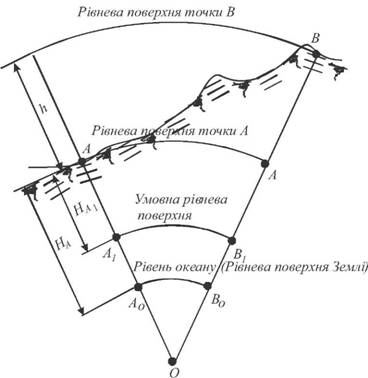
Картою називається зменшене і спотворене за рахунок кривизни Землі зображення горизонтальної проекції значної частини або всієї земної поверхні на аркуші паперу та побудоване за відповідними математичними законами. При зображенні на аркуші паперу горизонтальних проекцій значних ділянок Землі або всієї її поверхні, яку приймають за поверхню еліпсоїда оберту, кривизною рівневої поверхні нехтувати не можна. Тому горизонтальна проекція і її зменшене зображення на папері не будуть подібними. В залежності від призначення карти під час її побудови вибирається певна картографічна проекція. Картографічні проекції будуються за відповідними математичними законами, за якими горизонтальна проекція зображується на площині. За характером спотворення відомі рівновеликі і рівнокутні картографічні проекції. Рівновеликі дозволяють зобразити на карті площі великих ділянок місцевості. Рівнокутні (конформні) дозволяють зобразити картографічні проекції на карті без спотворення кутів між лініями місцевості. Якщо через точки А і В, які закріпленні на місцевості провести прямовисну площину, то отримаємо профіль місцевості за відповідним напрямком АВ (рис.4). На рис. 4: h - перевищення точки В над точкою А; Ha1- умовна висота точки А; Ha- абсолютна висота точки А. Зменшене зображення перетину земної поверхні на аркуші паперу теж називається профілем. Профіль місцевості зображують при проектуванні лінійних споруд та при вирішенні багатьох інженерних задач.
Рис. 4. Профіль місцевості
1.4. Визначення планового і висотного положення точки на земній поверхні Планове і висотне положення будь-якої точки розташованої на фізичній поверхні Землі визначається просторовими координатами. Так, точка А на сфері визначається географічними координатами: р - географічною широтою та X - географічною довготою її горизонтальної проекції та висотою Ha (рис. 4 і 5).
Рис. 5. Географічна система координат
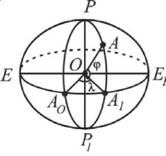
Географічною широтою у називається кут, який відлічується від площини екватору до прямовисної лінії, яка проходить через задану точку А на сфері і змінюється від 0° до 90°. Широта точки називається північною, якщо вона розташована в північній півкулі, і південною, якщо вона розташована в південній півкулі. Географічною довготою X називається кут, який відлічується від площини початкового меридіану, який проходить через Грінвіч до площини географічного меридіану, який проходить через дану точку А земної поверхні і змінюється від 0° до 180° на схід або захід в залежності від розташування точки на сфері. Довгота буває східною і західною. Географічні координати у і X на місцевості визначають шляхом астрономічних вимірювань. У вищій геодезії широко використовується система геодезичних координат на поверхні еліпсоїда (рис. 6).
Рис. 6. Геодезична система координат
Геодезичною широтою В називається кут, який відлічується від площини екватору до нормалі AO1 точки А на еліпсоїді оберту і змінюється від 0° до 90°. Широта буває північною і південною, в залежності від того в якій півкулі знаходиться точка.
Геодезичною довготою L називається кут, який відлічується від площини початкового меридіану (Грінвіч) до площини геодезичного меридіану, який проходить через дану точку A та змінюється від 0° до 180°. Довгота точок розташованих від початкового меридіану на схід (проти годинникової стрілки) називаються східною, а довгота точок розташованих від початкового меридіану на захід (за годинниковою стрілкою) називаються західною. Положення точки А розташованої на фізичній поверхні Землі визначається географічними координатами ф і X її горизонтальної проекції і висотою НА (рис. 4 і рис. 5). Висотою точки називається відстань від рівневої поверхні (поверхні прийнятої за 0,00 м) до верху знаку закріпленої точки. Висоти бувають абсолютні, умовні і відносні (або перевищення). Розрахунок абсолютних висот в нашій державі ведуть від нуля Кронштадтського футштоку. Назва футшток походить від поєднання англійського слова foot (фут) з німецьким stock (палиця, жердина). На рис. 4 точка А має абсолютну висоту НА, а умовна висота цієї точки буде Н. За умовну рівневу поверхню можна приймати будь-яку поверхню. Так в будівництві будівельники приймають за висоту ± 0,00 м поверхню, яка співпадає з рівнем чистої підлоги першого поверху кожної будівлі. Таким чином кожна будівля має свою початкову висоту. Висота однієї точки відносно висоти другої точки називається відносною або перевищенням і позначається буквою h. Таким чином, перевищення дорівнює різниці висот двох точок з абсолютними або відносними висотами. Геодезичні вимірювання, за результатами яких обчислюють перевищення між двома точками місцевості, називається нівелюванням. Вивчення топографічних карт Числовий масштаб Оскільки фігура Землі за своїми розмірами є надто великою, то виготовлення її моделі в натуральну величину неможливо. При виготовленні будь-якої моделі добиваються, щоб вона була подібна оригіналу в зменшеному або в збільшеному (що рідко трапляється) виді і з точністю похибок вимірювання. Щоб цього досягнути необхідно проектувати і будувати модель в горизонтальній проекції. Масштабом називається ступінь зменшення горизонтальних прокладень ліній місцевості при зображені їх на плані або карті. Масштаб записується дробовим числом. В чисельнику обов'язково ставлять одиницю, а в знаменнику число в скільки разів зменшується горизонтальне прокладення ліній на місцевості.
1:25 000. Таким чином, виміряна лінія на місцевості наноситься на план або карту в зменшеному виді відповідно у 500, 1000, 2000, 5000, 10 000 і 25 000 разів. Правдива і наступна інформація. Якщо на плані або карті викреслити відрізок довжиною 1 см, то цьому відрізку на місцевості буде відповідати відрізок 500, 1000, 2000, 5000, 10 000 і 25 000 см. Основна формула масштабу має наступний вигляд d = s X M, (13) де s -кількість сантиметрів на плані або карті; M - знаменник масштабу Задача 1. На карті масштабу 1:10 000 довжина відрізка s = 2,34 см. Визначити довжину відповідного йому горизонтального прокладання лінії на місцевості d. Згідно формули (13), отримаємо d = 2,34 см х10 000 = 23400 см =234 м. Задача 2. Довжина горизонтального прокладення лінії на місцевості d = 374 м. Визначити її довжину на карті масштабу 1:5000. За формулою (13) визначаємо s
На основі вище приведеного можна зробити наступні висновки. Чим більший знаменник M числового масштабу, тим масштаб мілкіший. Чим менший знаменник M числового масштабу, тим масштаб крупніший. Масштаб 1:50 000 мілкіший масштабу 1:25 000 в два рази, а масштаб 1:2000 крупніший масштабу 1:10 000 в п'ять разів. Лінійний масштаб При користуванні числовим масштабом необхідно виконувати певний обсяг обчислювальних робіт, а це при великих об'ємах значно обтяжливо. Тому часто користуються лінійним масштабом. Лінійний масштаб за своєю конструкцією простий у виготовлені та користуванні (рис. 9).
Рис. 9. Лінійний масштаб
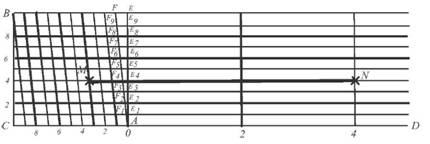
Для побудови на папері лінійного масштабу необхідно накреслити лінію CD, на якій відкласти відрізки однакової довжини, наприклад 2 см. Зліва одне ділення ділять на 10 частин і отримують десяті частини, які в свою чергу дорівнюють 2 мм. Кожних 2 мм поділили на дві частини і отримали величину найменшого ділення рівного 1 мм. Підписують лінійний масштаб згідно прийнятого числового масштабу. Для масштабу 1:5000 в двох сантиметрах на плані або карті буде відповідати на місцевості 100 м, а одне найменше ділення відповідає 5 м. Тому віддаль AB = 265 м. Одне велике ділення а = 2 см називається основою масштабу. Якщо основа відповідає 2 см, то такий масштаб називають нормальним. Лінійний масштаб за своєю точністю не перевищує 0,5 найменшого ділення масштабу плану. В нашому випадку ця точність буде становити 2,5 м. Як бачимо точність лінійного масштабу відповідно низька, а тому його можна використовувати безпосередньо при рекогностуванні місцевості під час побудови планового і висотного геодезичного обґрунтування, вибору площі для розробки проектів сівозмін, меліоративного осушення та зрошення територій, попереднього вибору осі автомобільної дороги і т. ін. Поперечний масштаб Поперечний масштаб є самим точним, а тому його постійно використовують в інженерних розрахунках. Будують лінійку поперечного масштабу наступним чином. На відрізку CD будують декілька основ масштабу а рівних 2 см (рис. 10). В точках фіксації основ встановлюють перпендикуляри і підписують 0, 2, 4, 6, і 8. Одну основу зліва від підписаного 0 лінійки ділять на 10 рівних поділок і отримують десяті частини основи. Для того, щоб отримати соті частини основи необхідно одну десяту частину поділити на 10 частин. Це досягається тим, що проводять десять ліній паралельних між собою і лінії CD та на однакових відстанях одна від другої. На верхній лінії від
Рис.10. Лінійка поперечного масштабу
перпендикуляру з підписом 0 відкладаємо величину відрізка рівного 0,1 частини основи. В нашому випадку таким відрізком буде FE. Точку F сполучають з точкою А і отримують трансверсаль AF. Через нанесені точки ділення на 10 частин відрізків CA і BF проводять паралельні лінії трансверсалі AF. Утворений прямокутний трикутник AEF поділений на 10 частин і кожна така частина є 0,01 вибраної основи. Таким чином відрізки відповідають сотим основі наступні: F1E1 = 0,01 CA; F4E4 = 0,04 CA; F7E7 = 0,07 CA; F2E2 = 0,02 CA; F5E5 = 0,05 CA; FgE8 = 0,08 CA; F3E2 = 0,03 CA; FfE6 = 0,06 CA; F9E9 = 0,09 CA. Для вимірювання віддалей між двома точками на топографічній карті поступають наступним чином. Одну ніжку вимірника ставлять в центр однієї точки, а другу ніжку вимірника ставлять в центр другої точки та не змінюючи розхилу вимірника кладуть його на лінію CD лінійки поперечного масштабу так, щоб одна ніжка співпала з перпендикуляром основи, а друга була обов'язково в районі десятих ділень основи. Пересувають розхил вимірника вверх і паралельно лінії CD так, щоб ніжка вимірника співпала з трансверсалю. Після цього рахують цілі основи, які відділяють комою і після коми записують кількість десятих та сотих. Досвідчені виконавці на око визначають тисячні долі основ. Наприклад, в нашому випадку між точками M і N на топографічному плані масштабу 1:5000 лінійці поперечного масштабу відповідає 2,34 основ (рис. 10). Оскільки основа має довжину 2 см, то її на місцевості буде відповідати 100 м. Щоб визначити скільки буде метрів між точками M і N на місцевості необхідно 2,34x100 м = 234 м. Згідно правилу віддаль визначають шляхом множення кількості основ на кількість метрів в одній основі, Таким чином відрізок MN приведений на лінійці поперечного масштабу для планів і карт різних масштабів буде відповідати різним віддалям (рис. 10). Наприклад, для нижче приведених масштабів віддалі, становлять: 1:500 відповідно 10 м x2,34 = 23,4 м; 1:1000 відповідно 20 м x2,34 =46,8 м; 1:2000 відповідно 40 м x2,34 = 93,60 м; 1:5000 відповідно 100 м x2,34 = 234 м; 1:10 000 відповідно 200 м x2,34 = 468 м; 1:25000 відповідно 500 м x2,34 = 1170 м. Точність масштабу В геодезичній практиці часто ставлять питання, а з якою точністю виконані виміри? Очевидно точність масштабу це відстань на місцевості яка відповідає довжині відстані найменшого відрізка, який людина може розпізнати на топографічному плані, або карті відповідного масштабу Відомо, що на плані можна розпізнати неозброєним оком відрізок довжиною 0,1 мм. Такий відрізок відповідає уколу зробленого гострою голкою на аркуші паперу. Тому довжина горизонтального прокладення лінії місцевості, яка відповідає на карті даного масштабу 0,1 мм, називається точністю масштабу. Так, точність масштабів 1:500, 1:1000, 1:2 000 і 1:5 000 дорівнює відповідно 0,05 м, 0,1 м, 0,2 м і 0,5 м. Орієнтування Введення в теорію похибок При самих якісних багатократних вимірюваннях однієї і тієї ж величини окремі результати дещо відрізняються між собою в ту чи іншу сторону від її дійсної величини. Все це відбувається через те, що процес вимірювання неминуче супроводжується похибками. Під похибкою результату виміру і розуміють різницю між цим результатом і точним (істинним) значенням X величини яку вимірюють, тобто
Вимірюючи будь-яку фізичну величину, ми не розраховуємо отримати її істинне значення. Все ж таки нам необхідно вказати, наскільки отриманий результат є близьким до істинного значення, тобто необхідно вказати точність вимірювання. Тому доцільно разом з отриманим результатом вказати наближену похибку вимірювання. Наприклад, ми виміряли стальною стрічкою довжину лінії AB, і отримали dAB =256,46 м. Відомо, що вимірювання виконані з відносною точністю 1:2000. Для визначення числового значення похибки виконують обчислення за формулою
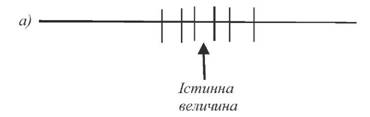
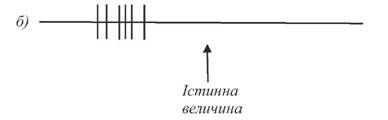
де M - граничний знаменник відносної похибки для виконання технічних робіт. Виміряну довжину лінії AB можна записати 256,56 ± 0,13 м. (25) Даний вираз означає, що виміряна довжина лінії AB знаходиться в межах 256,43 < 256,56 > 256,69. (26) В дійсності рівняння (26) має ймовірний сенс. Ми не можемо впевнено стверджувати, що дана величина лежить в зазначених межах, але наші вимірювання показують, що є деяка ймовірність цього. Визначати похибки необхідно тому, що не знаючи їх, не можна зробити відповідних висновків із проведених вимірювань. Отримані результати вимірів публікуються і стають загальним надбанням. Кожен може користуватися ними, як йому завгодно. Одні можуть використовувати його в розрахунках для практичної мети, інші - для перевірки теоретичних доведень. Якщо на основі отриманого результату роблять висновки, то важливо знати, в якій мірі можна на них покластися. Все це необхідне для того, щоб можна було відповісти на подібні запитання. Тому виконавець зобов'язаний вказати величину похибки вимірювання. Можна подумати, що будь-які вимірювання слід проводити якомога точніше, але такий підхід був би неправильним. Тому важливо планувати і виконувати вимірювання так, щоб точність кінцевих результатів відповідала їх меті. Таким чином поняття похибки вимірювання відіграє далеко не другорядну роль при вимірюваннях. Воно має пряме відношення до таких питань, як мета виміру, його метод і значимість та результативність. Види похибок вимірювання Під час геодезичних вимірювань виникають похибки від яких залежить точність отриманих результатів. Відомо, що точність вимірювань повинна бути пов'язана із граничними допусками передбаченими існуючими інструкціями, тому необхідно знати величини похибок і причини їх походження. Похибки бувають грубими, випадковими і систематичними. Грубі похибки виникають в результаті промахів при вимірюваннях або при обчисленнях. Теорія похибок вимірювань не розглядає грубі похибки (промахи), виникнення яких пов'язано з порушенням правил експлуатації приладів та некомпетенцією працівників і випадковими описками. Тому грубі похибки повинні повністю виключатися під час виявлення їх шляхом контрольних вимірювань і обчислень. Так, згідно Інструкції горизонтальний кут, перевищення і віддаль вимірюють два рази, відповідно при КП і при КЛ, по чорній і червоній сторонах рейки, в прямому і зворотньому напрямках. Вимірювання і обчислення контролюють також шляхом обчислення нев'язки, наприклад, кутової в ходах полігонометрії, нівелірних ходах, в приростах координат і т.д. Систематичні похибки виникають за рахунок одноманітної і безперервної дії спотворення кінцевого результату вимірів в процесі вимірювання. Систематичною похибкою називається похибка, яка залишається постійною на протязі всієї серії вимірювань. Інколи систематичні похибки непостійні. Наприклад, рулетка 20-метрова виявилася на 20 см довшою. Все це виникло через те, що під час нанесення ділень на полотно стрічки замість величини 1 м нанесли величину 1,01 м. Тоді, 20 х 1,01 м= 20,20м. Похибка даної рулетки є великою, в цьому випадку слід відмовитися від використання її або кожен раз вводити поправку у виміри. Ось чому виконують компарування мірних приладів. До того ж нерідко в такому процесі вимірювань існують декілька причин появи систематичних похибок і не всі із них вдається вивчити і виявити повністю. Випадковими похибками називають такі, поява яких не залежить від нашої волі. Випадкові похибки при вимірах неминучі і причин при їх виникненні існує декілька та неможливо встановити їх дію. Тому завжди визначають, як впливають вони на кінцевий результат вимірів. Випадкові похибки змінюють свій знак в рівній мірі як на додатній так і на від'ємний. При відсутності систематичних похибок вони служать причиною розподілення повторних вимірів відносно істинного значення (рис. 38).
Рис.38. Наявність тільки випадкових похибок
Якщо дана величина буде налічувати і систематичну похибку, то результати вимірів будуть розподілені відносно не істинного, а зміщеного значення (рис. 39).
Рис. 39. Наявність не тільки випадкових, але і систематичних похибок
Нехай виміряли лінію багато разів, похибка відліку за штрихом невелика, але нерівномірність зумовлена тим що натяг стрічки не однаковий в усіх вимірах, присутня шерехатість місцевості та зміна температури стрічки під час вимірювань - все це викликає розподілення результатів повторних вимірювань і тому їх відносять до виду випадкових похибок. Дослідженнями встановлено, що при всіх однакових умовах вимірювань будь-якої одної величини випадкові похибки мають наступні властивості: 1. За абсолютною своєю величиною вони не будуть перевищувати будь-якої граничної величини. Чим більша абсолютна величина випадкової похибки, тим рідше вона з'являється в даному ряді вимірів. Похибки із знаком плюс з'являються так же часто, як із знаком мінус. Середнє арифметичне із випадкових похибок на основі третьої властивості, буде необмежено наближатися до нуля із збільшенням числа вимірів даної величини. На основі цієї властивості випадкових похибок можна стверджувати, що середнє арифметичне із результатів вимірів одної і тої ж величини буде наближатися до істинного значення цієї величини при збільшені числа вимірів в силу компенсації похибок з різними знаками. Тому вважають, що середнє арифметичне із результатів, навіть невеликого числа вимірів, буде ближче до істинного значення, ніж будь-який окремо взятий результат. На цій основі середнє арифметичне із результатів вимірів прийнято називати ймовірнішим значенням виміряної величини, а розходження кожного виміру із середнім арифметичним - ймовірнішою похибкою. Згідно третьої властивості випадкових похибок вимірювання її можна виразити математично. Так, при вимірюванні п разів величини X отримали результати іі, і2, із,..., іп, а випадкові похибки цих вимірів становлять відповідно Al, А2, A3,..., Ап, то можна це виразити формулою
або
[Ai]= J1 + J2 + A3 +... + An. (29) Нехай ми виконуємо серію вимірів одної і тої ж величини без систематичних похибок. Із-за наявності випадкових похибок окремі значення -C j, -C2, -C3,..., -Cn, неоднакові, і в якості найкращого значення шуканої величини приймається середнє арифметичне Xo Нерівноточні виміри величии Коли величину вимірюють різними приладами з різною точністю або прийомами, то кінцевий результат буде нерівноточним. При обчисленні середнього значення із нерівноточних результатів враховують вагу кожного результату. Вага - це число, яке характеризує точність будь-якого результату по відношенню до інших результатів. Середнє арифметичне із нерівноточних вимірів називають загальною арифметичною серединою або середнім ваговим. Нехай при вимірюванні лінії отримали п кінцевих результатів. Отримані результати відрізняються між собою тільки числом вимірів. P1 раз і отримали середній (кінцевий) результат dj P2 раз і отримали середній (кінцевий) результат d2 P3 раз і отримали середній (кінцевий) результат d3 рп раз і отримали середній (кінцевий) результат dn Тоді вагове середнє обчислюють за формулою
Приклад. Виміряна одна і та ж лінія три, два і чотири рази. Середні значення довжини лінії отримали наступні: У випадку, коли b = h, mb = mh = m; dj = 234,76; d2 = 234,70; d3 = 234,74. Знайти середнє вагове. В довільній формі призначають d' =234,65, та обчислюють різниці
Встановлено, що вага виміру обернено пропорційна квадрату середньої квадратичної похибки, тобто
Загальна вага арифметичної середини дорівнює сумі ваг окремих груп вимірів, тобто
При оцінці точності нерівноточних вимірів використовують поняття про середню квадратичну похибку вимірювання, вага якого рівна одиниці
де § - відхилення від середнього вагового результату кожної групи вимірів. Наприклад S1 = do- di; S2 = do- d2; S3 = do- d3; і т. д. Середня квадратична похибка середнього вагового обчислюється за формулою
Наприклад, необхідно обчислити середню квадратичну похибку ваги і загальної арифметичної середини за результатами вище приведеного прикладу табл^ Таблиця 3
9 +2 44 1 • Обчислюють середню квадратичну похибку вимірювання
2. Обчислюють середню квадратичну похибку середнього вагового Кінцевий результат середнього вагового d =234,74 ± 0,008 м; o Відносна середня квадратична похибка обчислюється за формулою
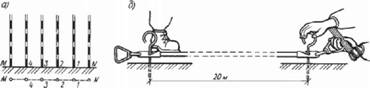
Вимірювання довжин ліній Вимірювання довжин ліній Вимірювання довжин ліній сталевою 20-метровою стрічкою або рулеткою відбувається при умові, що вона вкладається послідовно від початкового до кінцевого пункту. Цю роботу виконують два чоловіки. Один з них називається переднім, а другий - заднім міряльником. Порядок вимірювань наступний. Задній мірник устромлює в землю шпильку в початковій точці А лінії АВ, стає на коліно, та притримує початок стрічки і зачіплює її вирізом за шпильку Передній мірник бере інші десять шпильок і іде вперед по лінії АВ, тримаючи другий кінець стрічки. Задній, продовжує тримати правою рукою початок стрічки без шпильки, а рухами лівої руки направляє переднього по створу лінії. Передній, дивлячись на сигнали заднього, в створі лінії АВ, утримує стрічку і слідкує за тим, щоб вона лягла прямо, не зачіплюючись за траву, і з силою 98,07Н (10 кг с) натягує її. Нарешті стрічка лежить в створі лінії АВ. По сигналу заднього мірника "Є!" передній вставляє шпильку в виріз стрічки проти штриха і устромляє її в землю, потім бере ручку стрічки і іде вперед (рис.42). Задній виймає шпильку в точці А і бере за ручку стрічки іде за
Рис. 42. Вимірювання лінії стальною стрічкою: а - провішування лінії; б - вимірювання лінії
переднім, підходить до шпильки, яку тільки що устромив передній, і командує: "Стій!". Прикладає стрічку вирізом до шпильки і знову направляє переднього мірника по створу лінії AB. Таким чином прокладається одна стрічка за другою вздовж лінії до тих пір, поки всі одинадцять шпильок не будуть у заднього мірника. Потім він передає десять шпильок передньому мірнику. Не важко здогадатися, що це відбувається через кожні 200м. Коли вся лінія виміряна, задній мірник підходить до точки B, причому ще до цього передній мірник повинен протягнути стрічку мимо точки B, потім вернутися, прикласти до точки стрічку і подивитись, або як говорять "взяти відлік" на стрічці з точністю до сантиметра. Після цього рахують кількість шпильок у заднього мірника (без шпильки, яка встромлена в землю). Нехай довжина виміряного відрізка становить 6 м 56 см, а в руці заднього мірника дві шпильки і мінявся він шпильками з переднім тільки один раз. Вираховуємо
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1012; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.27.88 (0.015 с.) |


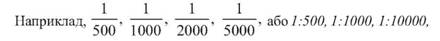
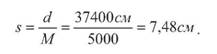
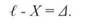 (23)
(23)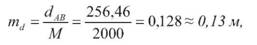 (24)
(24)

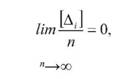
 ' (48)
' (48)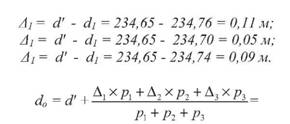
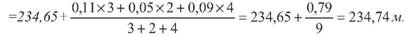
 (49)
(49)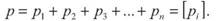 (50)
(50)