Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Систематические линейные блочные коды (слбк)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные понятия Линейные коды – коды, для которых поразрядная сумма по модулю два любых разрешенных кодовых комбинаций также является разрешенной кодовой комбинацией. Линейные коды называют также групповыми. Они задаются с помощью порождающей
где
Матрица С помощью матрицы Если две порождающие матрицы различаются только порядком расположения столбцов, то определяемые ими коды называются эквивалентными. Они имеют одинаковые кодовые расстояния и, следовательно, одинаковые способности обнаруживать и исправлять ошибки. Пример 3.1: Код Рида-Маллера (8, 4) задается следующей порождающей матрицей:
Матрица Чаще всего применяют систематические линейные коды. Такие коды задаются матрицами в систематической (приведено-ступенчатой или канонической) форме:
где
Пример 3.2: Систематический код Рида-Маллера (8, 4) задается порождающей матрицей:
Найдем проверочную матрицу:
Кодирование информации 1) С помощью матрицы
где Пример 3.3: Рассмотрим кодирование информационного слова
2) С помощью матрицы Единицы в Пример 3.4: Из матрицы
Тогда для Код с четным числом единиц Это простейший систематический код с параметрами Порождающая и проверочная матрицы такого кода:
Уравнение кодирования: Этот код имеет Коды хэмминга Это линейные блочные коды с параметрами Они обладают кодовым расстоянием Примеры полных кодов Хэмминга: (7, 4), (15, 11), (31, 26), (63, 57). Пример 3.5: Рассмотрим код Хэмминга (7, 4). Проверочная матрица:
Порождающая матрица:
Модификациями кодов Хэмминга являются укороченные и удлиненные коды Хэмминга. Чтобы получить проверочную матрицу укороченного кода Хэмминга, необходимо в проверочной матрице полного кода исключить любые Т столбцов, относящиеся к информационным разрядам, где Т - параметр укорочения. Удлиненные коды Хэмминга получаются путем введения дополнительной проверки на четность всех символов кодового слова. Коды Хэмминга обладают очень слабой корректирующей способностью и отдельно практически не используются. Очень хорошие результаты позволяет получить применение данных кодов в составе каскадных схем кодирования. Каскадные коды состоят из двух или более кодов: кодовые слова одного кода являются информационными символами для кода следующей ступени.
ЦИКЛИЧЕСКИЕ КОДЫ Основные понятия Поиск более простых процедур кодирования и декодирования привел к появлению циклических кодов. Циклические коды – линейные блочные коды, обладающие свойством цикличности: если Пример 4.1:
Для построения кода достаточно задать одно кодовое слово. Другие кодовые слова образуются из исходного путем циклических перестановок и их линейных преобразований. Все преобразования кодовых слов циклических кодов производятся в виде математических операций над полиномами (многочленами). Для этого кодовые слова представляются в форме полиномов:
где
Пример 4.2:
Операции сложения, вычитания, умножения и деления полиномов выполняются по обычным арифметическим правилам, только вычитание заменяется сложением, которое производится как сложение по модулю два. Циклические коды задаются с помощью порождающего (образующего) Любой полином
где Полиномы всех кодовых слов делятся без остатка на порождающий полином. Порождающая матрица строится на основе полинома Для несистематического циклического кода:
Для систематического циклического кода:
где Пример 4.3: Показать, что полином
Для несистематического кода:
Для систематического кода:
Результат деления полинома вида
где При отсутствии ошибок в принятом кодовом слове
Проверочная матрица строится на основе полинома Для несистематического циклического кода:
Для систематического циклического кода:
ДОМАШНЕЕ ЗАДАНИЕ: 2. Найти полином
Кодирование информации Существует два способа кодирования: - несистематическое кодирование:
где
- систематическое кодирование:
где Пример 4.3: Закодировать слово Несистематическое кодирование:
Систематическое кодирование: 1) 2) 3) Кодирующие устройства Их основу составляют схемы умножения и деления полиномов, основными элементами которых являются триггерная ячейка, сумматор по модулю два, умножитель на скаляр. Правила построения схем умножения и деления: - число ячеек памяти равно старшей степени полинома - число сумматоров на единицу меньше веса полинома
- при умножении множимое подается одновременно на вход и на все сумматоры, при делении делимое подается только на первый сумматор, а частное на выход и на все сумматоры. Множимое и делимое поступает на вход, начиная со старшего разряда.
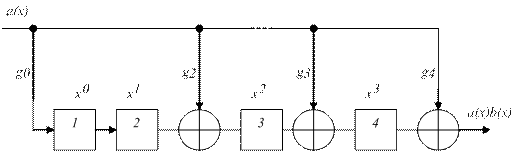
Рисунок 4.1 – Кодер несистематического циклического кода. Кодер реализует алгоритм
Кодер реализует алгоритм Пример 4.4: 1 Построить схему кодера циклического кода из примера 4.3.
Рисунок 4.3 – Кодер несистематического кода. 2 Схему кодера систематического кода построить самостоятельно.
ДОМАШНЕЕ ЗАДАНИЕ: 1. [3.1.2] с.315…318; [3.1.3] с.200…204; [3.1.5] с.149…150; [3.1.14] с.263…270, 282…286.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1403; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.1.100 (0.008 с.) |

 и проверочной
и проверочной 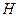 матриц, которые связаны основным уравнением кодирования:
матриц, которые связаны основным уравнением кодирования: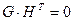 ,
, - транспонированная проверочная матрица (строки
- транспонированная проверочная матрица (строки 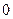 - нулевая матрица.
- нулевая матрица. строк и
строк и 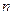 столбцов, ее элементами являются нули и единицы. Строками матрицы
столбцов, ее элементами являются нули и единицы. Строками матрицы 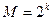 кодовых слов длины
кодовых слов длины 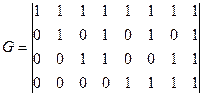 .
. строк и
строк и 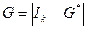 ,
,
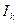 ,
,  - единичные подматрицы размерностью
- единичные подматрицы размерностью  и
и 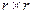 соответственно;
соответственно;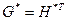 - прямоугольная подматрица размерностью
- прямоугольная подматрица размерностью 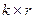 ;
;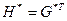 - прямоугольная подматрица размерностью
- прямоугольная подматрица размерностью 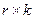 .
.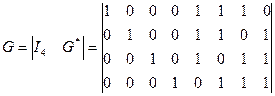 .
.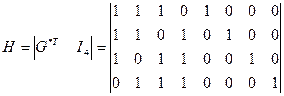 .
.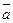 на порождающую матрицу
на порождающую матрицу 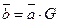 ,
, - кодовый вектор.
- кодовый вектор.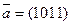 кодом Рида-Маллера (8, 4):
кодом Рида-Маллера (8, 4): =(11000011).
=(11000011). -ой строке подматрицы
-ой строке подматрицы  указывают, какие информационные символы необходимо просуммировать по модулю два, чтобы получить
указывают, какие информационные символы необходимо просуммировать по модулю два, чтобы получить 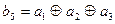 ,
,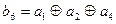 ,
, ,
, .
.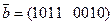 .
. . Он строится добавлением к комбинации из
. Он строится добавлением к комбинации из  ,
, .
. .
. и позволяет обнаруживать любое нечетное число ошибок.
и позволяет обнаруживать любое нечетное число ошибок.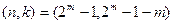 , где
, где 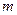 - положительное целое число,
- положительное целое число, 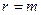 - число проверочных символов. Для задания кодов Хэмминга обычно используется проверочная матрица. Ее столбцами являются все ненулевые двоичные числа длиной
- число проверочных символов. Для задания кодов Хэмминга обычно используется проверочная матрица. Ее столбцами являются все ненулевые двоичные числа длиной 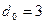 и способны исправлять только одну или обнаруживать две ошибки.
и способны исправлять только одну или обнаруживать две ошибки.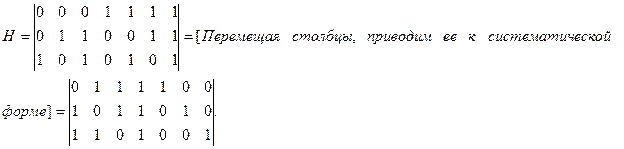
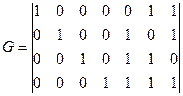 .
. - кодовое слово циклического кода, то его циклическая перестановка
- кодовое слово циклического кода, то его циклическая перестановка  также является кодовым словом.
также является кодовым словом.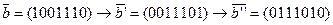 .
. ,
,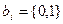 - коэффициенты полинома;
- коэффициенты полинома;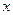 - символическая переменная.
- символическая переменная.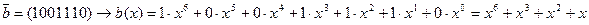 .
.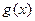 и проверочного
и проверочного 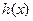 полиномов.
полиномов.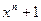 , называется порождающим полиномом:
, называется порождающим полиномом: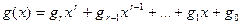 ,
,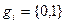 - коэффициенты полинома.
- коэффициенты полинома.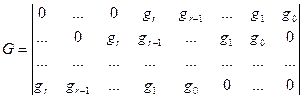 .
. ,
, - прямоугольная подматрица
- прямоугольная подматрица  на полином
на полином  является порождающим для 7-разрядного циклического кода. Записать матрицу
является порождающим для 7-разрядного циклического кода. Записать матрицу 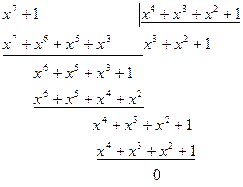
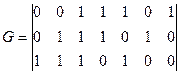 .
.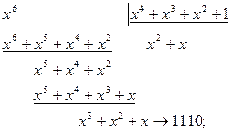
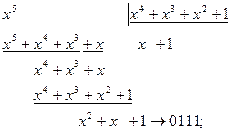
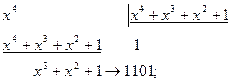
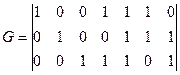 .
.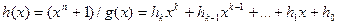 ,
,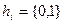 - коэффициенты полинома.
- коэффициенты полинома. остаток от деления произведения
остаток от деления произведения  на полином вида
на полином вида  .
.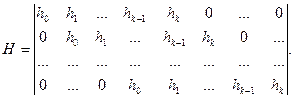
 .
.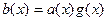 ,
, - полином информационного слова,
- полином информационного слова, - полином кодового слова;
- полином кодового слова; ,
, - остаток от деления произведения
- остаток от деления произведения 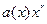 на полином
на полином 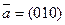 циклическим кодом из примера 4.3.
циклическим кодом из примера 4.3.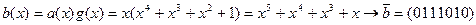 .
. ;
;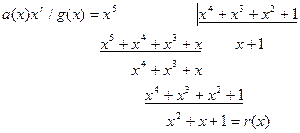 ;
;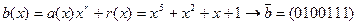 .
.
 последующих тактов при отсутствии информационных символов на входе происходит очищение ячеек регистра. При этом на выходе, на каждом из
последующих тактов при отсутствии информационных символов на входе происходит очищение ячеек регистра. При этом на выходе, на каждом из 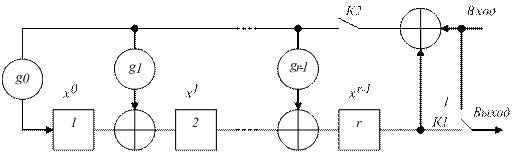
 находится в положении 1, а ключ
находится в положении 1, а ключ  замкнут. Информационные символы, подаваемые на вход, через ключ
замкнут. Информационные символы, подаваемые на вход, через ключ  - в кодирующее устройство, где через
- в кодирующее устройство, где через