
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Декодирование линейных кодовСодержание книги
Поиск на нашем сайте Существует три основных метода декодирования линейных кодов: - декодирование по максимуму правдоподобия (по минимуму расстояния); - мажоритарное декодирование (по большинству проверок); - декодирование по синдрому. Декодирование по максимуму правдоподобия Правило декодирования: В качестве переданного слова
Рисунок 5.1 – Структурная схема декодера по минимуму расстояния. На рисунке: УСр – устройство сравнения; ГКС – генератор кодовых слов; РУ – решающее устройство. Данный метод используется, когда число информационных символов Мажоритарное декодирование Основано на том, что каждый информационный символ можно выразить через другие символы кодового слова с помощью линейных соотношений. Окончательное решение о значении символа принимается по мажоритарному принципу (по большинству) результатов таких проверок. Существует три способа построения систем проверочных уравнений для декодирования символа: - системы с разделенными проверками – символ, относительно которого разделяется система, входит во все уравнения. Любой другой символ входит не более, чем в одно уравнение. Для коррекции - системы с - системы с квазиразделенными проверками – система разделима относительно некоторой суммы символов. На первом этапе она разрешается относительно суммы символов, а на втором – относительно конкретного символа.
Рисунок 5.2 – Структурная схема мажоритарного декодера. На рисунке: 1…k – устройства, реализующие проверки для соответствующей системы; МЭ – мажоритарный элемент, принимающий решение о значении символа по большинству результатов проверок. Пример 5.1: Код (8,4) задан матрицей:
Система уравнений по матрице Н:
Система проверочных уравнений для
Система проверочных уравнений для
Система проверочных уравнений для
Система проверочных уравнений для
Пусть
Результат декодирования: Декодирование по синдрому Основано на стандартной таблице – таблице всех возможных принятых из канала слов, организованной таким образом, что может быть найдено ближайшее к принятому кодовое слово. Она содержит Таблица – Стандартная таблица.
b i – кодовые слова; e j – векторы ошибок – образцы ошибок минимального веса; b i+ e j – слова, не являющиеся кодовыми; s i= e i∙HT – синдромы – векторы размерностью r, указывающие на наличие и расположение ошибок в принятом слове. Правило декодирования: 1. Вычисляется синдром
Если 2. По 3. Ближайшее к принятому кодовое слово
Рисунок 5.3 – Структурная схема декодера по синдрому. На рисунке: Б – буфер хранения принятого слова; БВС – блок вычисления синдрома; С – селектор (дешифратор) синдрома; К – корректор. Данный метод используется, когда число проверочных символов Пример: Составить стандартную таблицу для систематического кода (5,2) с порождающей матрицей:
Таблица должна содержать Таблица – Стандартная таблица.
Пусть 1. 2. 3. ДОМАШНЕЕ ЗАДАНИЕ: 1. [3.1.2] с. 309…312, 317…318; [3.1.3] с. 205…208; [3.1.5] с. 147.. 149, 150…151; [3.1.14] с. 258…261, 271…273. 2. Код (7,4) задан порождающей матрицей:
Провести декодирование по синдрому принятого слова
6 НЕПРЕРЫВНЫЕ (РЕКУРРЕНТНЫЕ) КОДЫ Общие сведения Непрерывные коды используют непрерывную обработку информации короткими фрагментами. Кодер для непрерывного кода обладает памятью, т.е. символы на его выходе зависят не только от очередного фрагмента информационных символов на входе, но и предыдущих символов на его входе и (или) выходе. Поэтому коды называются рекуррентными (recur – возвращаться, повторяться). Эти коды применяют для обнаружения и исправления пакетов ошибок. Пакет ошибок – ошибка, затрагивающая цепочку символов. Описывается длиной Пример 6.1: Пакеты ошибок длиной 4 могут быть такими:
К непрерывным кодам относят цепной и сверточные. Цепной код является простейшим случаем сверточных.
Цепной код В таком коде после каждого информационного символа следует проверочный. Закодированная последовательность имеет вид:
где
Код позволяет исправить пачки ошибок длиной Сверточные коды (ск) Это линейные, рекуррентные коды. Название обусловлено тем, что кодирование информации СК представляет собой операцию свертки двух функций:
где
Набор порождающих полиномов определяет внутреннюю конструкцию кодера.
Рисунок 6.1 – Обобщенная структурная схема кодера СК. Кодирующее устройство содержит На практике чаще используются коды с единственным входным потоком ( Пример 6.2:
Рисунок 6.2 – Структурная схема кодера несистематического СК с
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 следует выбирать слово, которое ближе всего по Хэммингу к принятому
следует выбирать слово, которое ближе всего по Хэммингу к принятому  .
.
 мало (
мало (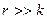 ).
). ошибок необходимо
ошибок необходимо  уравнений в системе;
уравнений в системе; -связанными проверками – символ, относительно которого разрешается система, входит во все уравнения. Любой другой символ входит не более, чем в
-связанными проверками – символ, относительно которого разрешается система, входит во все уравнения. Любой другой символ входит не более, чем в  уравнений в системе;
уравнений в системе;
 .
.
 :
:
 :
: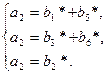
 :
:
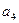 :
:
 .
.

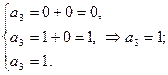

 .
. строк и
строк и  столбцов.
столбцов. по принятому слову
по принятому слову  .
. , то
, то  )
)  .
.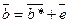 .
.
 мало (<10).
мало (<10). .
. строк и
строк и 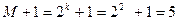 столбцов.
столбцов. (10111). Проведем декодирование.
(10111). Проведем декодирование.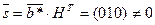 ;
; ;
; .
. .
. .
. и вектором ошибок
и вектором ошибок 

 - шаг сложения. Определяет корректирующие возможности кода;
- шаг сложения. Определяет корректирующие возможности кода; - информационные символы;
- информационные символы; - проверочные символы. Формируются по правилу:
- проверочные символы. Формируются по правилу: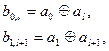

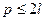 , если они разделены защитным интервалом
, если они разделены защитным интервалом  .
.
 - входная последовательность информационных символов;
- входная последовательность информационных символов;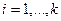 - номер входа;
- номер входа; - выходная последовательность кодовых символов;
- выходная последовательность кодовых символов; - номер выхода;
- номер выхода; - порождающий полином.
- порождающий полином.
 -ого регистра сдвига определяется старшей степенью полинома
-ого регистра сдвига определяется старшей степенью полинома 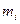 . Коэффициенты полинома
. Коэффициенты полинома  определяют связи между двоичными разрядами
определяют связи между двоичными разрядами  -ым выходом кодера.
-ым выходом кодера. ) поэтому индекс
) поэтому индекс 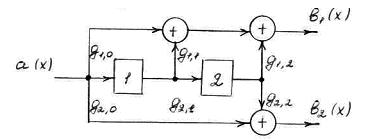
 и
и  .
.


