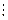Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система передачи дискретных сообщенийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
КОДИРОВАНИЕ СИГНАЛОВ 1.1 основные понятия Кодирование – преобразование элементов дискретного сообщения в последовательности кодовых символов. Обратное преобразование – декодирование. Устройства, осуществляющие эти операции автоматически, называются соответственно кодером и декодером. Кодек – устройство, объединяющее кодер и декодер. Код – алгоритм (правило), по которому осуществляется кодирование. Кодовая комбинация (слово) – последовательность кодовых символов, соответствующая одному элементу дискретного сообщения. Кодовый алфавит – весь набор кодовых символов. Основание кода m – число символов в кодовом алфавите. Если m=2 код называется двоичным, m>2 – многопозиционным (недвоичным). Разряд – значащая позиция кодового слова. Разрядность (значность) кода n – число символов в кодовой комбинации. Если n =const, то код называется равномерным, n≠const – неравномерным. Кодеры и декодеры легче сделать для равномерных двоичных кодов.
Система передачи дискретных сообщений
Рисунок 1.1 – Структурная схема системы передачи дискретных сообщений.
Источник выдает дискретное сообщение. Для формирования дискретного сообщения из непрерывного используется дискретизация по времени и по уровню. Кодирование источника (сжатие данных) применяется для снижения технических затрат на хранение и передачу информации. Криптографическое кодирование (шифрование) применяется для предотвращения несанкционированного доступа к информации. Кодирование канала (помехоустойчивое кодирование) применяется для повышения достоверности передачи информации по каналу с помехами.
Сжатие данных Сжатие возможно, т.к. данные на выходе источника содержат избыточную и/или плохо различимую информацию. Плохо различимая информация - информация, которая не воздействует на ее приемник. Подобная информация сокращается или удаляется при использовании сжатия с потерями. При этом энтропия исходной информации уменьшается. Сжатие с потерями применяется при сжатии цифровых изображений и оцифрованного звука. Приемы, применяемые в алгоритмах сжатия с потерями: - использование модели – подбор параметров модели и передача только одних параметров;
- предсказание – предсказание последующего элемента и передача величины ошибки; - дифференциальное кодирование – передача изменений последующего элемента при сравнении с предыдущим. Избыточная информация – информация, которая не добавляет знаний о предмете. Избыточность может быть уменьшена или устранена с помощью сжатия без потерь (эффективного кодирования). При этом энтропия данных остается неизменной. Сжатие без потерь применяется в системах передачи данных. Приемы, применяемые в алгоритмах сжатия без потерь: - кодирование длин последовательностей – передача числа повторяющихся элементов; - кодирование словаря – использование ссылок на переданные ранее последовательности, а не их повторение; - неравномерное кодирование – более вероятным символам присваиваются более короткие кодовые слова. Кодирование словаря Позволяет уменьшить избыточность, вызванную зависимостью между символами. Идея кодирования словаря состоит в замене часто встречающихся последовательностей символов ссылками на образцы, хранящиеся в специально создаваемой таблице (словаре). Данный подход основан на алгоритме LZ, описанном в работах израильских исследователей Зива и Лемпеля. Неравномерное кодирование Позволяет уменьшить избыточность, вызванную неравной вероятностью символов. Идея неравномерного кодирования состоит в использовании коротких кодовых слов для часто встречающихся символов и длинных – для редко возникающих. Данный подход основан на алгоритмах Шеннона-Фано и Хаффмана. Коды Шеннона-Фано и Хаффмана являются префиксными. Префиксный код – код, обладающий тем свойством, что никакое более короткое слово не является началом (префиксом) другого более длинного слова. Такой код всегда однозначно декодируем. Обратное неверно. Код Шеннона-Фано строится следующим образом. Символы источника выписываются в порядке убывания вероятностей (частот) их появления. Затем эти символы разбиваются на две части, верхнюю и нижнюю, так, чтобы суммарные вероятности этих частей были по возможности одинаковыми. Для символов верхней части в качестве первого символа кодового слова используется 1, а нижней – 0. Затем каждая из этих частей делится еще раз пополам и записывается второй символ кодового слова. Процесс повторяется до тех пор, пока в каждой из полученных частей не останется по одному символу.
Пример1.1: Таблица 1.1 – Построение кода Шеннона-Фано.
Алгоритм Шеннона-Фано не всегда приводит к построению однозначного кода с наименьшей средней длиной кодового слова. От отмеченных недостатков свободен алгоритм Хаффмана. Код Хаффмана строится следующим образом. Символы источника располагают в порядке убывания вероятностей (частот) их появления. Два самых последних символа объединяют в один вспомогательный, которому приписывают суммарную вероятность. Полученные символы вновь располагают в порядке убывания вероятностей, а два последних объединяют. Процесс продолжается до тех пор, пока не останется единственный вспомогательный символ с вероятностью 1. Для нахождения кодовых комбинаций строится кодовое дерево. Из точки, соответствующей вероятности 1, направляются две ветви. Ветви с большей вероятностью присваивается символ 1, с меньшей – 0. Такое ветвление продолжается до достижения вероятности каждого символа. Двигаясь по кодовому дереву сверху вниз, записывают для каждого символа кодовую комбинацию.
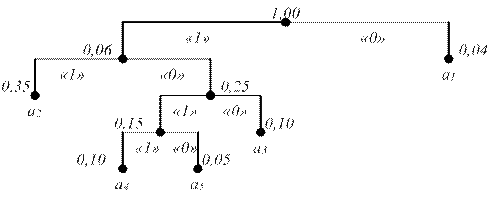
Пример1.2: Таблица 1.2 – Построение кода Хаффмана.
Рисунок 1.2 – Кодовое дерево для кода Хаффмана.
Домашнее задание: 1. [3.1.2] с.13…16; [3.1.3] с.174…176; [3.1.5] с. 109…112, 131…135, 297…299; [3.1.14] с. 146…155; [3.1.15] с.11…14. 2. Файл состоит из некоторой символьной строки: «aaaaaaaaaabbbbbbbbccccccdddddeeeefff». Закодировать символы кодами Шеннона-Фано и Хаффмана и оценить достигнутую степень сжатия.
РЕШЕНИЕ ЗАДАЧИ ДОМАШНЕГО ЗАДАНИЯ: Рассчитаем частоты появления символов: υ (а)=10/36=0,28; υ (b)=8/36=0,22; υ (c)=6/36=0,17; υ (d)=5/36=0,14; υ (e)=4/36=0,11; υ (f)=0,08. Таблица 1.3 – Построение кода Шеннона-Фано.
Достигнутая в результате кодирования степень сжатия определяется коэффициентом сжатия:
где к0 – первоначальный размер данных; кm – размер данных в сжатом виде. При кодировании кодом Шеннона-Фано обеспечивается коэффициент сжатия:
где 36 – количество символов в файле; ¯| log2 6|¯ - минимальная длина кодовой комбинации при кодировании равномерным кодом (¯|.|¯ обозначает ближайшее целое число, большее log 26); 10, 8, 6, 5, 4, 3 – число символов a, b, c, d, e, f в файле; 2, 2, 3, 3, 3, 3 – длина кодовых комбинаций кода Шеннона-Фано, соответствующих символам a, b, c, d, e, f (см. таблицу 1.1). Таблица 1.3 – Построение кода Хаффмана.
Рисунок 1.3 – Кодовое дерево для кода Хаффмана. При кодировании кодом Хаффмана обеспечивается степень сжатия: Ксж =36∙¯| log2 6|¯/(10∙2+8∙2+6∙3+5∙3+4∙3+3∙3)=108/90=1,2.
Код с постоянным весом Это неразделимый блочный код, каждая кодовая комбинация которого имеет одинаковое число единиц (одинаковый вес). Если вес принятой кодовой комбинации отличается от заданного, то выносится решение об ошибке. Данный код обладает Пример 2.3: Таким кодом является код МТК-3 – семиразрядный код, каждая кодовая комбинация которого содержит три единицы. ДОМАШНЕЕ ЗАДАНИЕ: 1 [3.1.1] с.272…277; [3.1.2] с.307…313; [3.1.3] с.185…189, 193; [3.1.5] с.137…144; [3.1.14] с.49…52; [3.1.15] с.12…23. 2. Составить кодовые комбинации четырехразрядного кода, если каждая из них имеет вес два. Привести пример переданного и принятого кодового слова, если произошла ошибка смещения.
Основные понятия Линейные коды – коды, для которых поразрядная сумма по модулю два любых разрешенных кодовых комбинаций также является разрешенной кодовой комбинацией. Линейные коды называют также групповыми. Они задаются с помощью порождающей
где
Матрица С помощью матрицы Если две порождающие матрицы различаются только порядком расположения столбцов, то определяемые ими коды называются эквивалентными. Они имеют одинаковые кодовые расстояния и, следовательно, одинаковые способности обнаруживать и исправлять ошибки. Пример 3.1: Код Рида-Маллера (8, 4) задается следующей порождающей матрицей:
Матрица Чаще всего применяют систематические линейные коды. Такие коды задаются матрицами в систематической (приведено-ступенчатой или канонической) форме:
где
Пример 3.2: Систематический код Рида-Маллера (8, 4) задается порождающей матрицей:
Найдем проверочную матрицу:
Кодирование информации 1) С помощью матрицы
где Пример 3.3: Рассмотрим кодирование информационного слова
2) С помощью матрицы Единицы в Пример 3.4: Из матрицы
Тогда для Код с четным числом единиц Это простейший систематический код с параметрами Порождающая и проверочная матрицы такого кода:
Уравнение кодирования: Этот код имеет Коды хэмминга Это линейные блочные коды с параметрами Они обладают кодовым расстоянием Примеры полных кодов Хэмминга: (7, 4), (15, 11), (31, 26), (63, 57). Пример 3.5: Рассмотрим код Хэмминга (7, 4). Проверочная матрица:
Порождающая матрица:
Модификациями кодов Хэмминга являются укороченные и удлиненные коды Хэмминга. Чтобы получить проверочную матрицу укороченного кода Хэмминга, необходимо в проверочной матрице полного кода исключить любые Т столбцов, относящиеся к информационным разрядам, где Т - параметр укорочения. Удлиненные коды Хэмминга получаются путем введения дополнительной проверки на четность всех символов кодового слова. Коды Хэмминга обладают очень слабой корректирующей способностью и отдельно практически не используются. Очень хорошие результаты позволяет получить применение данных кодов в составе каскадных схем кодирования. Каскадные коды состоят из двух или более кодов: кодовые слова одного кода являются информационными символами для кода следующей ступени. ЦИКЛИЧЕСКИЕ КОДЫ Основные понятия
Поиск более простых процедур кодирования и декодирования привел к появлению циклических кодов. Циклические коды – линейные блочные коды, обладающие свойством цикличности: если Пример 4.1:
Для построения кода достаточно задать одно кодовое слово. Другие кодовые слова образуются из исходного путем циклических перестановок и их линейных преобразований. Все преобразования кодовых слов циклических кодов производятся в виде математических операций над полиномами (многочленами). Для этого кодовые слова представляются в форме полиномов:
где
Пример 4.2:
Операции сложения, вычитания, умножения и деления полиномов выполняются по обычным арифметическим правилам, только вычитание заменяется сложением, которое производится как сложение по модулю два. Циклические коды задаются с помощью порождающего (образующего) Любой полином
где Полиномы всех кодовых слов делятся без остатка на порождающий полином. Порождающая матрица строится на основе полинома Для несистематического циклического кода:
Для систематического циклического кода:
где Пример 4.3: Показать, что полином
Для несистематического кода:
Для систематического кода:
Результат деления полинома вида
где При отсутствии ошибок в принятом кодовом слове
Проверочная матрица строится на основе полинома Для несистематического циклического кода:
Для систематического циклического кода:
ДОМАШНЕЕ ЗАДАНИЕ: 2. Найти полином
Кодирование информации Существует два способа кодирования: - несистематическое кодирование:
где
- систематическое кодирование:
где Пример 4.3: Закодировать слово Несистематическое кодирование:
Систематическое кодирование: 1) 2) 3) Кодирующие устройства Их основу составляют схемы умножения и деления полиномов, основными элементами которых являются триггерная ячейка, сумматор по модулю два, умножитель на скаляр. Правила построения схем умножения и деления: - число ячеек памяти равно старшей степени полинома - число сумматоров на единицу меньше веса полинома - при умножении множимое подается одновременно на вход и на все сумматоры, при делении делимое подается только на первый сумматор, а частное на выход и на все сумматоры. Множимое и делимое поступает на вход, начиная со старшего разряда.
Рисунок 4.1 – Кодер несистематического циклического кода. Кодер реализует алгоритм
Кодер реализует алгоритм Пример 4.4: 1 Построить схему кодера циклического кода из примера 4.3.
Рисунок 4.3 – Кодер несистематического кода. 2 Схему кодера систематического кода построить самостоятельно.
ДОМАШНЕЕ ЗАДАНИЕ: 1. [3.1.2] с.315…318; [3.1.3] с.200…204; [3.1.5] с.149…150; [3.1.14] с.263…270, 282…286. Мажоритарное декодирование Основано на том, что каждый информационный символ можно выразить через другие символы кодового слова с помощью линейных соотношений. Окончательное решение о значении символа принимается по мажоритарному принципу (по большинству) результатов таких проверок. Существует три способа построения систем проверочных уравнений для декодирования символа: - системы с разделенными проверками – символ, относительно которого разделяется система, входит во все уравнения. Любой другой символ входит не более, чем в одно уравнение. Для коррекции - системы с - системы с квазиразделенными проверками – система разделима относительно некоторой суммы символов. На первом этапе она разрешается относительно суммы символов, а на втором – относительно конкретного символа.
Рисунок 5.2 – Структурная схема мажоритарного декодера. На рисунке: 1…k – устройства, реализующие проверки для соответствующей системы; МЭ – мажоритарный элемент, принимающий решение о значении символа по большинству результатов проверок. Пример 5.1: Код (8,4) задан матрицей:
Система уравнений по матрице Н:
Система проверочных уравнений для
Система проверочных уравнений для
Система проверочных уравнений для
Система проверочных уравнений для
Пусть
Результат декодирования: Декодирование по синдрому Основано на стандартной таблице – таблице всех возможных принятых из канала слов, организованной таким образом, что может быть найдено ближайшее к принятому кодовое слово. Она содержит Таблица – Стандартная таблица.
b i – кодовые слова; e j – векторы ошибок – образцы ошибок минимального веса; b i+ e j – слова, не являющиеся кодовыми; s i= e i∙HT – синдромы – векторы размерностью r, указывающие на наличие и расположение ошибок в принятом слове. Правило декодирования: 1. Вычисляется синдром
Если 2. По 3. Ближайшее к принятому кодовое слово
Рисунок 5.3 – Структурная схема декодера по синдрому. На рисунке: Б – буфер хранения принятого слова; БВС – блок вычисления синдрома; С – селектор (дешифратор) синдрома; К – корректор. Данный метод используется, когда число проверочных символов Пример: Составить стандартную таблицу для систематического кода (5,2) с порождающей матрицей:
Таблица должна содержать Таблица – Стандартная таблица.
Пусть 1. 2. 3. ДОМАШНЕЕ ЗАДАНИЕ: 1. [3.1.2] с. 309…312, 317…318; [3.1.3] с. 205…208; [3.1.5] с. 147.. 149, 150…151; [3.1.14] с. 258…261, 271…273. 2. Код (7,4) задан порождающей матрицей:
Провести декодирование по синдрому принятого слова
6 НЕПРЕРЫВНЫЕ (РЕКУРРЕНТНЫЕ) КОДЫ Общие сведения Непрерывные коды используют непрерывную обработку информации короткими фрагментами. Кодер для непрерывного кода обладает памятью, т.е. символы на его выходе зависят не только от очередного фрагмента информационных символов на входе, но и предыдущих символов на его входе и (или) выходе. Поэтому коды называются рекуррентными (recur – возвращаться, повторяться). Эти коды применяют для обнаружения и исправления пакетов ошибок. Пакет ошибок – ошибка, затрагивающая цепочку символов. Описывается длиной Пример 6.1: Пакеты ошибок длиной 4 могут быть такими:
К непрерывным кодам относят цепной и сверточные. Цепной код является простейшим случаем сверточных.
Цепной код В таком коде после каждого информационного символа следует проверочный. Закодированная последовательность имеет вид:
где
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

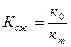 ,
, 36∙¯| log2 6|¯/(10∙2+8∙2+6∙3+5∙3+4∙3+3∙3)=108/90=1,2,
36∙¯| log2 6|¯/(10∙2+8∙2+6∙3+5∙3+4∙3+3∙3)=108/90=1,2,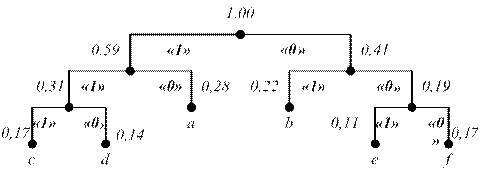
 и обнаруживает все ошибки нечетной кратности и часть ошибок четной кратности (не обнаруживаются только ошибки смещения, когда число искаженных единиц равно числу искаженных нулей).
и обнаруживает все ошибки нечетной кратности и часть ошибок четной кратности (не обнаруживаются только ошибки смещения, когда число искаженных единиц равно числу искаженных нулей). и проверочной
и проверочной  матриц, которые связаны основным уравнением кодирования:
матриц, которые связаны основным уравнением кодирования: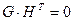 ,
, - транспонированная проверочная матрица (строки
- транспонированная проверочная матрица (строки 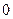 - нулевая матрица.
- нулевая матрица. строк и
строк и 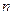 столбцов, ее элементами являются нули и единицы. Строками матрицы
столбцов, ее элементами являются нули и единицы. Строками матрицы 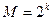 кодовых слов длины
кодовых слов длины 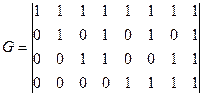 .
. строк и
строк и 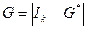 ,
,
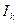 ,
,  - единичные подматрицы размерностью
- единичные подматрицы размерностью  и
и 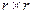 соответственно;
соответственно;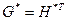 - прямоугольная подматрица размерностью
- прямоугольная подматрица размерностью 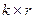 ;
;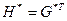 - прямоугольная подматрица размерностью
- прямоугольная подматрица размерностью 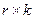 .
.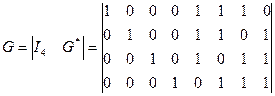 .
.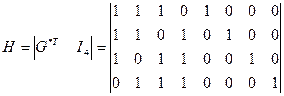 .
.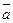 на порождающую матрицу
на порождающую матрицу 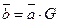 ,
, - кодовый вектор.
- кодовый вектор.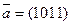 кодом Рида-Маллера (8, 4):
кодом Рида-Маллера (8, 4): =(11000011).
=(11000011). -ой строке подматрицы
-ой строке подматрицы  указывают, какие информационные символы необходимо просуммировать по модулю два, чтобы получить
указывают, какие информационные символы необходимо просуммировать по модулю два, чтобы получить 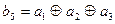 ,
,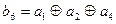 ,
, ,
, .
.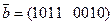 .
. . Он строится добавлением к комбинации из
. Он строится добавлением к комбинации из  ,
, .
. .
. и позволяет обнаруживать любое нечетное число ошибок.
и позволяет обнаруживать любое нечетное число ошибок.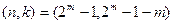 , где
, где 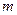 - положительное целое число,
- положительное целое число, 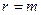 - число проверочных символов. Для задания кодов Хэмминга обычно используется проверочная матрица. Ее столбцами являются все ненулевые двоичные числа длиной
- число проверочных символов. Для задания кодов Хэмминга обычно используется проверочная матрица. Ее столбцами являются все ненулевые двоичные числа длиной 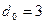 и способны исправлять только одну или обнаруживать две ошибки.
и способны исправлять только одну или обнаруживать две ошибки.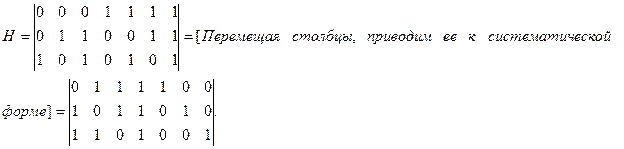
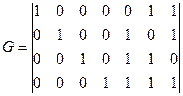 .
. - кодовое слово циклического кода, то его циклическая перестановка
- кодовое слово циклического кода, то его циклическая перестановка  также является кодовым словом.
также является кодовым словом.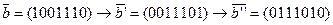 .
. ,
,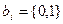 - коэффициенты полинома;
- коэффициенты полинома;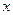 - символическая переменная.
- символическая переменная.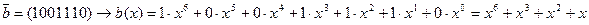 .
.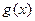 и проверочного
и проверочного 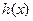 полиномов.
полиномов.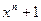 , называется порождающим полиномом:
, называется порождающим полиномом: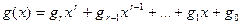 ,
,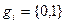 - коэффициенты полинома.
- коэффициенты полинома.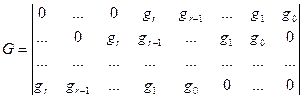 .
. ,
, - прямоугольная подматрица
- прямоугольная подматрица 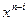 на полином
на полином  является порождающим для 7-разрядного циклического кода. Записать матрицу
является порождающим для 7-разрядного циклического кода. Записать матрицу 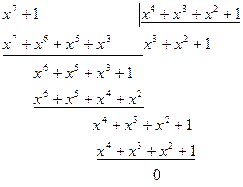
 .
.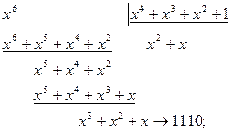
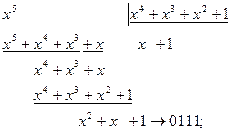
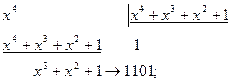
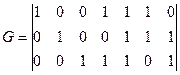 .
.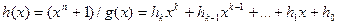 ,
,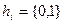 - коэффициенты полинома.
- коэффициенты полинома. остаток от деления произведения
остаток от деления произведения  на полином вида
на полином вида  .
.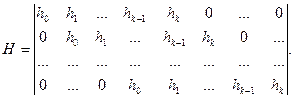
 .
.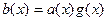 ,
,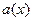 - полином информационного слова,
- полином информационного слова, - полином кодового слова;
- полином кодового слова; ,
,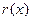 - остаток от деления произведения
- остаток от деления произведения 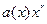 на полином
на полином 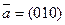 циклическим кодом из примера 4.3.
циклическим кодом из примера 4.3.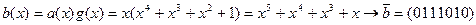 .
. ;
;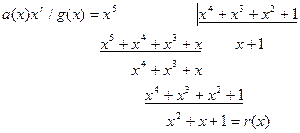 ;
;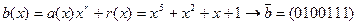 .
.
 последующих тактов при отсутствии информационных символов на входе происходит очищение ячеек регистра. При этом на выходе, на каждом из
последующих тактов при отсутствии информационных символов на входе происходит очищение ячеек регистра. При этом на выходе, на каждом из 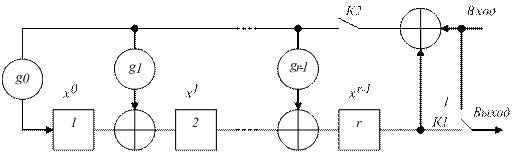
 находится в положении 1, а ключ
находится в положении 1, а ключ 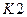 замкнут. Информационные символы, подаваемые на вход, через ключ
замкнут. Информационные символы, подаваемые на вход, через ключ 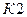 - в кодирующее устройство, где через
- в кодирующее устройство, где через 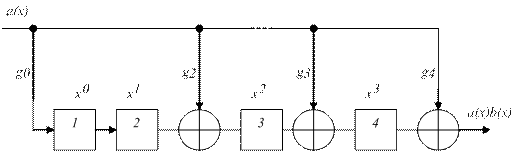
 ошибок необходимо
ошибок необходимо  уравнений в системе;
уравнений в системе; -связанными проверками – символ, относительно которого разрешается система, входит во все уравнения. Любой другой символ входит не более, чем в
-связанными проверками – символ, относительно которого разрешается система, входит во все уравнения. Любой другой символ входит не более, чем в  уравнений в системе;
уравнений в системе;
 .
.
 :
:
 :
: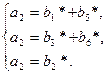
 :
:
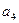 :
:
 .
.

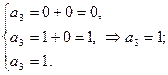

 .
. строк и
строк и  столбцов.
столбцов. по принятому слову
по принятому слову  .
. , то
, то  )
)  .
.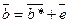 .
.
 .
. строк и
строк и 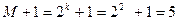 столбцов.
столбцов. (10111). Проведем декодирование.
(10111). Проведем декодирование.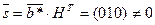 ;
; ;
; .
. .
. .
. и вектором ошибок
и вектором ошибок 

 - шаг сложения. Определяет корректирующие возможности кода;
- шаг сложения. Определяет корректирующие возможности кода; - информационные символы;
- информационные символы; - проверочные символы. Формируются по правилу:
- проверочные символы. Формируются по правилу: