Тема. Решение задач оптимизации внешнеэкономических операций средствами ппп MS Excel.

 

Пусть некоторое предприятие продает n различных видов товаров. Обозначим через х₁, х₂ …, х_n неизвестные количества товаров первого, второго и т.д. n-го вида, которые должны быть определены в результате решения задачи. Для реализации этих n изделий предприятию необходимы m видов ресурсов, которые отпускаются ему в количествах b₁,b₂…, b_m. Обозначим через а₁₁ количество ресурсов первого вида, которое расходуется при продаже единицы товара первого вида, через а₁₂ – количество ресурса первого вида, которое расходуется при продаже единицы товара второго вида и т.д. Таким образом, a есть количество ресурса i- го вида, которое расходуется при продаже единицы товара j- го вида. Таким образом, величины a и x по смыслу не могут быть отрицательными.

Сравнивая затраты каждого вида ресурса, расходуемого при продаже товаров, с имеющимся количеством ресурсов, приходим к системе неравенств:

а₁₁ х_{1 +} а₁₂ х_{2 +… +}а_1n х_n £ b₁,

... (1)

а_m1 х_{1 +} а_m2 х_{2 +… +}а_mn х_n £ b_m,

где х_i³ 0 (1 £ і £ n).

Экономический смысл этих неравенств заключается в том, что затраты каждого ресурса не могут превосходить его наличия.

Обозначим через c ₁ прибыль, получаемую от реализации единицы товара первого вида через с₂ - прибыль от реализации единицы товара второго вида и т.д. Общая прибыль от реализации всех товаров тогда составит f= c ₁ х_{1 +} с₂ х₂ + … +с_nх_n

Требуется определить значения всех неизвестных, обеспечивающих максимальную прибыль данному предприятию:

_{® max (2)}

 

Сформулированная задача в виде целевой функции (2) при условиях (1) является задачей линейного программирования, являющейся подвидом задач оптимального программирования (оптимизационные задачи).

Оптимальным программированием принято называть процесс поиска наилучших с той или иной точки зрения решений. Задача оптимального программирования формулируется по разному.

Наиболее просто задача оптимального программирования формулируется на уровне отlельного предприятия. В систему показателей деятельности торгового предприятия входят ассортимент товаров, площадь торговых залов и подсобных помещений, вид торгового оборудования, количество и квалификация работников и др. все эти показатели отдельным образом влияют на рентабельность работы предприятия. При составлении планов деятельности требуется правильно учитывать их влияние и сопоставлять различные варианты плана с целью выбора наилучшего, исходя из определенного критерия. Таким критерием может быть прибыль. Тогда оптимальным будет план, который при заданных значениях всех показателей обеспечивает максимальную прибыль. Если в качестве критерия выбраны издержки обращения, то оптимальным будет план, обеспечивающий минимум издержек обращения.

Обобщая выводы, сделанные выше, можно кратко сформулировать принцип оптимальности в экономике следующим образом:

оптимальным является план, обеспечивающий максимальный эффект при использовании заданного объема ресурсов или заданный результат при минимальных затратах.

Задачи линейного программирования решаются графическим методом (при числе переменных не больше трех) или симплексным методом.

Пример.

Пусть торговое предприятие продает два вида товаров (А, В) в количествах х₁, х_2, используя при этом два вида ресурсов: рабочее время продавцов в количестве 420ч. и площадь торгового зала 80 кв.м. Пусть известны плановые нормативы затрат этих ресурсов в расчете на единицу товаров А и В и прибыль от продажи (таб.5.1). Необходимо определить оптимальную структуру товарооборота, обеспечивающую торговому предприятию максимум прибыли.

 

Таблица 5.1.

Показатели	Товар А	Товар В
Расход рабочего времени на единицу товара, ч	0.6	0.7
Использование площади торгового зала на единицу товара, кв.м.	0.1	0.2
Прибыль от продажи единицы товара, грн.

 

Решение:

Ограничения задачи перепишется в виде

0.6 х₁ +0,7 х₂ £ 420;

0.1х₁ +0.2 х₂ £ 80.

где х_i³ 0. Требуется найти значения х₁, х₂ обеспечивающие max {f= 5х₁ +8 х₂ }

 

1) Запустить программу Excel.Оформить исходные данные в виде рис.5.1.

 

	A	B	C	D	E
	Переменные:				Целевая функция:
	х1=		х2=		=5*B2+8*D2
	=0,6*B$2+0,7*D$2
	=0,1*B$2+0,2*D$2

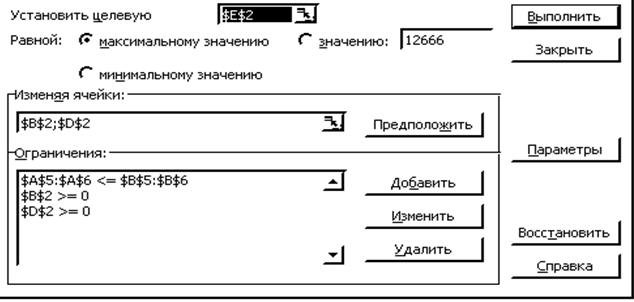
Рис.5.1

2) Выполнить команду Сервис – Поиск решения

3) Заполнить строки в появившемся диалоговом окне, как показано на рис.5.2.

В процедуре поиска решения Microsoft Excel используются алгоритмы симплексного метода и метода «branch-and-bound» для решения линейных и целочисленных задач с ограничениями и.алгоритм нелинейной оптимизации Generalized Reduced Gradient (GRG2),

 

 

Рис.5.2

 

Диалоговое окно процедуры «Поиск решения» в меню программы «Сервис», позволяет изменять условия и варианты поиска решения для линейных и нелинейных задач, а также загружать и сохранять оптимизируемые модели, однако значения и состояния элементов управления, используемые по умолчанию, подходят для решения большинства задач.

Выбрав вкладку «Параметры», откроется диалоговое окно «Параметры поиска решения», которое имеет следующие возможности:

- Максимальное время – используется для ограничения времени, отпускаемого на поиск решения задачи.

- Итерации – используется для управления временем решения задачи, путем ограничения числа промежуточных вычислений.

- Точность – используется для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам.

- Допустимое отклонение – используется для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. При указании большего допуска поиск решения заканчивается быстрее.

- Сходимость – если относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле «Сходимость», поиск прекращается. Сходимость применяется только к нелинейным задачам, условием служит дробь из интервала от 0 (нуля) до 1.

- Линейная модель - используется для ускорения поиска решения линейной задачи оптимизации или линейной аппроксимации нелинейной задачи.

- Показывать результаты итераций - для приостановки поиска решения и просмотра результатов отдельных итераций.

- Автоматическое масштабирование - для включения автоматической нормализации входных и выходных значений.

- Значения неотрицательны - установка нулевой нижней границы для тех влияющих ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение.

- Оценка - для указания метода экстраполяции ѕ линейная или квадратичная ѕ используемого для получения исходных оценок значений переменных в каждом одномерном поиске.

- Линейная - использование линейной экстраполяции вдоль касательного вектора.

- Квадратичная - использование квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.

- Производные – указывает метод численного дифференцирования.

- Прямые - применяется для гладких непрерывных функций.

- Центральные - для функций, имеющих разрывную производную.

- Метод - выбор алгоритма оптимизации (метод Ньютона или сопряженных градиентов) для указания направление поиска.

- Загрузить модель - задает ссылку на область ячеек, содержащих загружаемую модель.

Варианты индивидуальных заданий.

Задание І. В соответствии с вариантом задания (таб.5.2) определить максимальное и минимальное значения целевой функции F(X) и значения аргументов, при которых они получены. Для всех предложенных вариантов: X1³0, X2³0. Распечатать лист, содержащий исходные данные и отчеты, предусмотренные командами средств «Поиска решений».

 

Таблица 5.2

 

№ варианта	Условия	№ варианта	Условия	№ варианта	Условия
	1X1 + 2X2 £ 10 -2X1 + 3X2 £ 6 4X1 + 6X2 ³ 24 1X 1+ 1X2 = F		7X1 + 2X2 ³14 5X1 + 6X2 £ 30 3X1 + 8X2 ³ 24 -2X1 + 5X2 = F		3X1 + 1X2 ³ 9 1X1 + 2X2 £ 8 1X1 + 6X2 ³ 12 4X1 + 6X2 = F
	4X1+2X2£12 -1X1 + 3X2 £ 6 2X1 + 4X2 ³ 8 1X1 + 2X2 = F		7X1 + 2X2 ³ 14 -1X1 + 2X2 £ 2 4X1 + 6X2 £ 24 3X1 - 2X2 = F		2X1 + 1X2 £ 10 -2X1 + 3X2 £ 6 2X1 + 4X2 ³ 8 2X1 + 3X2 = F

 

				Продолжение таблицы 5.2
	-4X1 +6X2 £ 24 2X1 – 4X2 £ 8 6X1 + 8X2 £ 48 -2X1 + 1X2 = F		2X1 + 2X2 ³ 4 6X1 + 8X2 £ 48 2X1 – 2X2 £ 4 5X1 + 4X2 = F		4X1 + 5X2 £ 20 2X1 – 3X2 ³ -6 1X1 + 4X2 ³ 4 3X1 + 3X2 = F
	2X1 + 1X2 £10 -1X1 + 2X2 £ 2 2X1 + 4X2 ³ 8 1X1 + 1X2 = F		2X1 + 3X2 £ 18 1X1 – 2X2 £ 2 2X1 – 1X2 ³ 6 4X1 + 2X2 =F		4X1 + 4X2 £ 16 1X1 + 2X2 ³ 2 -1X1 +1X2 £ -1 2X1 + 5X2 = F

Задание ІІ. Решить транспортную задачу.

Вариант 1.

Рассмотрим еще один пример, где используется средство поиска решений. Предположим, что фирма имеет 4 фабрики и 5 центров распределения ее то­варов. Фабрики фирмы располагаются в Денвере, Бостоне, Новом Орлеане и Далласе с производственными возможностями 200, 150, 225 и 175 единиц продукции ежедневно, соответственно. Центры распределения товаров фир­мы располагаются в Лос-Анджелесе, Далласе, Сент-Луисе, Вашингтоне и Атланте с потребностями в 100, 200, 50, 250 и 150 единиц продукции еже­дневно, соответственно. Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в табл. 5.3. Необходимо так спланировать перевозки, чтобы минимизировать суммар­ные транспортные расходы.

Таблица 5.3.

Транспортные расходы

 

		Лос-Анджелес	Даллас	Сент-Луис	Вашингтон	Атланта
	Денвер	1.5		1.75	2.25	2.25
	Бостон	2.5		1.75		1.5
	Новый Орлеан		1.5	1.5	1.75	1.75
	Даллас		0.5	1.75	1.75	1.75

Вариант 2.

Пусть с трех складов требуется перевезти грузы в объемах 50, 30, и 40 тонн на 2 торговые подразделения в объеме 40 и 80 тонн. Известна цена перевозки единицы груза с каждого склада в каждый пункт доставки, соответственно: 10, 20, 15 грн./т и 5, 25, 10 грн./т (столбцы С и Е). Определить такие объемы перевозок со складов в пункты доставки, при которых стоимость транспортировки была минимальной. Данные представить в виде таб.5.4. Распечатать таблицу решения задачи в формульном и обычном режимах.

 

Таблица 5.4.

	A	B	C	D	E	F
			Торговое подразделение 1	Торговое подразделение 2
	Наличие груза на складах	Цена перевозки	Объем груза	Цена перевозки	Объем груза
	склад1			*		*
	склад2			*		*
	склад3			*		*
	ВСЕГО	*
	Целевая функция:	*

Вместо символа * должны быть введены формулы или результаты вычислений.

Задание ІІІ. Линейная оптимизационная задача.

Вариант 1.

Пусть перед некоторым инвестором стоит проблема принятия решения о вложе­нии имеющегося у него капитала. Построить оптимизационную модель, определяющую объекты инвестирования, при которых достигается наибольшее значение прибыли и одновременно выполняются ограничения на структуру портфеля активов. Набор характеристик потенциальных объектов для инвестирования, имеющих условные имена от А до F, задается в табл. 5.5.Предполагается, что при принятии решения о приобретении активов должны быть соблюдены следующие условия:

1. Суммарный объем капитала, который должен быть вложен, составляет
$100 000.

2. Доля средств, вложенная в один объект, не может превышать четверти от всего объема.

3. Более половины всех средств должны быть вложены в долгосрочные активы
(допустим, на рассматриваемый момент к таковым относятся активы со сроком погашения после 2004 года).

4. Доля активов, имеющих надежность менее чем 4 балла, не может превышать трети от суммарного объема.

Таблица 5.5.

Параметры активов.

 

Название	Доходность, в %	Срок выкупа, год	Надежность, баллы
A	5.5
B	6.0
C	8.0
D	7.5
E	5.5
F	7.0

Вариант 2.

Фирма имеет возможность рекламировать свою продукцию, используя местные радио и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены суммой 1000 долл. в месяц. Каждая минута радиорекламы обходится в 5 долл., каждая минута телерекламы – 100 долл. Фирма хотела бы использовать радиосеть по крайней мере в два раза чаще, чем телевидение. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше объема сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио и телерекламой.

Лабораторная работа № 6