
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретические основы статистикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ОГЛАВЛЕНИЕ 1. Теоретические основы статистики …………………………………………....... 5 1.1. Понятие статистики ……………………………………………………….. 5 1.2. Предмет статистики ……………………………………………………….. 5 1.3. Статистическая совокупность ……………………………………………. 6 1.4. Статистический показатель ………………………………………………. 7 1.5. Методы статистического исследования …………………………………. 7 1.6. Организация государственной статистики в Российской Федерации …. 8 2. Статистическое наблюдение …………………………………………………….. 9 2.1. Формы статистического наблюдения ……………………………………. 9 2.2. Виды статистического наблюдения ……………………………………… 9 2.3. Способы статистического наблюдения …………………………………. 11 2.4. Контроль статистического наблюдения ………………………………… 11 3. Статистическая сводка …………………………………………………………. 13 3.1. Понятие, виды и этапы сводки ………………………………………….. 13 3.2. Программа и план сводки ……………………………………………….. 13 3.3. Предварительный контроль материалов ……………………………….. 13 3.4. Понятие и виды группировки данных ………………………………….. 14 3.5. Проведение первичной группировки (количество интервалов, виды интервалов) ………………………………………………………………………. 15 3.6. Вторичная группировка ………………………………………………….. 17 4. Статистические показатели ……………………………………………………. 19 4.1. Понятие и классификация статистических показателей ………………. 19 4.2. Абсолютные показатели …………………………………………………. 20 4.3. Относительные показатели ……………………………………………… 20 4.4. Система статистических показателей ……………………………………21 4.5. Функции статистических показателей ………………………………….. 22 5. Представление статистических данных ……………………………………… 23 5.1. Статистические ряды распределения …………………………………… 23 5.2. Статистические таблицы ………………………………………………… 24 5.3. Статистические графики ………………………………………………… 24 6. Средние величины и показатели вариации ………………………………….. 29 6.1. Понятие средней величины ……………………………………………… 29 6.2. Средняя арифметическая и ее свойства ………………………………… 29 6.3. Другие виды средних величин и их соотношения ……………………... 31 6.4. Структурные характеристики (мода, медиана, квартили, децили) …… 33 6.5. Показатели размера вариации …………………………………………… 36 6.6. Показатели асимметрии и эксцесса распределения …………………… 38 7. Выборочное наблюдение ……………………………………………………….. 40 7.1. Понятие и причины использования выборочного метода …………….. 40 7.2. Виды и схемы отбора ……………………………………………………… 7.3. Определение объема выборки ……………………………………………… 7.4. Ошибка выборки …………………………………………………………… 7.5. Распространение данных выборочного наблюдения на генеральную совокупность ……………………………………………………………………… 7.6. Этапы проведения выборочного наблюдения малых предприятий в РФ 8. Ряды динамики ……………………………………………………………………47 9.1. Понятие рядов динамики ………………………………………………… 47 9.2. Показатели динамики ……………………………………………………. 47 9.3. Средние показатели динамики ………………………………………….. 48 9.4. Анализ основной тенденции в рядах динамики ………………………... 49 9.5. Измерение устойчивости в динамике …………………………………... 52 9. Индексы ………………………………………………………………………….....54 9.1. Понятие и виды индексов ………………………………………………... 54 9.2. Индивидуальные индексы ……………………………………………….. 54 9.3. Агрегатные индексы ……………………………………………………... 55 9.4. Средневзвешенные индексы …………………………………………….. 57 9.5. Индексы средней величины ……………………………………………... 57 10. Статистическая проверка гипотез …………………………………………… 60 10.1. Понятие статистической гипотезы …………………………………….. 60 10.2. Теоретические кривые распределения ………………………………… 61 10.3. Проверка гипотез о характере распределения ………………………… 63 11. Изучение взаимосвязей между явлениями ………………………………….. 65 11.1. Основные понятия ………………………………………………………. 65 11.2. Показатели взаимосвязи качественных переменных ………………… 65 11.3. Показатели взаимосвязи количественных переменных ……………… 67 11.4. Определение параметров парной линейной регрессии ………………. 69 11.5. Оценка надежности параметров парной линейной регрессии ……….. 70 Список рекомендуемой литературы ……………………………………………... 73
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СТАТИСТИКИ Понятие статистики Статистика – наука, изучающая количественную сторону массовых социально-экономических явлений с целью выявления их качественных особенностей и закономерностей. Статистика осуществляет следующие функции: сбор, обобщение, представление, анализ и интерпретация массовых данных. Статистика делится на: 1. Общая теория статистики. 2. Социально-экономическая статистика. 3. Отраслевые статистики. Общая теория статистики разрабатывает понятийный аппарат, систему категорий статистической науки, рассматривает общую методологию статистического исследования массовых общественных процессов. Таким образом, общая теория статистики - методологическая основа всех отраслевых статистик. Основными задачами статистики являются: 1) всестороннее исследование происходящих в обществе глубоких преобразований экономических и социальных процессов на основе научно обоснованной системы показателей; 2) обобщение и прогнозирование тенденций развития народного хозяйства; 3) выявление имеющихся резервов эффективности общественного производства; 4) своевременное обеспечение надежной информацией законодательной власти, управленческих, исполнительных и хозяйственных органов, а также широкой общественности.
Предмет статистики Предмет статистики: количественная сторона массовых социально-экономических явлений. Данные, с которыми приходится работать в статистике, делятся на три типа: 1) пространственные данные (N→∞, t=1) – данные об однородных объектах за один и тот же период времени: финансовые отчеты предприятий за определенный квартал или год, результаты обследования домашних хозяйств за период, данные о ВВП различных стран в каком-либо конкретном году и т.п. 2) временные ряды (N=1, t→∞) – последовательные значения одной экономической переменной в различные периоды времени: ежедневные значения курса доллара по отношению к рублю за период с 1 января 2007 г. до 1 сентября 2008 г., значения ВВП России за год в период с 1993 до 2007 г., и т.п. 3) панельные данные (N→∞, 1< t <∞) – до некоторой степени обобщение временных рядов и пространственных данных. Например, если с одних и те же предприятий каждый год собираются одни и те же показатели их хозяйственной деятельности, получится массив данных, в котором содержатся и данные об однородных объектах за один и тот же период времени, и последовательные значения одной экономической переменной в различные периоды времени (ежегодный объем выпуска продукции за период 1995 по 2007 гг. по 10 крупнейшим предприятиям угледобывающей отрасли).
Статистическая совокупность Статистическая совокупность – множество социально-экономических объектов или явлений общественной жизни, объединенных некой качественной основой, общей связью, но отличающихся друг от друга отдельными признаками. Пример: совокупность домохозяйств, семей, предприятий, фирм, городов области и т.д. Совокупности могут быть однородными и разнородными. Совокупность однородная, если один или несколько изучаемых существенных признаков ее объектов являются общими для всех единиц. Например, мужской пол, возраст 18-25 лет, малые предприятия, предприятия торговли и т.д. Совокупность разнородная, если в нее входят явления разного типа. Совокупность может быть однородна в одном отношении и разнородна в другом: например, торговые предприятия любого размера (малые, средние, крупные). Единица совокупности – отдельная, первичная, неделимая часть совокупности, обладающая признаками, подлежащими регистрации, и основой ведущегося при обследовании счета. Признак совокупности – качественная особенность единицы совокупности. Например, признаки человека: возраст, пол, образование и т.д.; признаки предприятия: форма собственности, отрасль, численность занятых, эффективность и т.д. Классификация признаков: 1) по характеру выражения - атрибутивные (описательные), - количественные а) альтернативные (принимают только два значения), б) дискретные (принимают только целочисленные значения), в) непрерывные (принимают любые значения), 2) по способу измерения - первичные (измеряются, считаются, взвешиваются…), - вторичные (рассчитываются), 3) по отношению к характеризуемому объекту - прямые (непосредственно присущи объекту), - косвенные (опосредованно присущи объекту), 4) по отношению ко времени - моментные (характеризуют объект в один момент времени), - интервальные (характеризуют результаты процессов за период времени) Важной чертой любой статистической совокупности является наличие вариации – изменение величины либо значения признака при переходе от одной единицы совокупности к другой. Если изменения изучаемого явления происходят в разные периоды времени и носят характер закономерности, то говорят о динамике признака. Статистические закономерности устанавливаются с помощью закона больших чисел: при определенных условиях (наличие вероятностных процессов, независимость, большое число факторов) совместное действие большого числа случайных факторов приводит к результатам практически независящим от случая.
Статистический показатель Статистика применяет не числа, а показатели. Статистический показатель – число, характеризующее ту или иную особенность признака или явления. Основными задачами в этом направлении являются: 1) правильное определение содержания статистического показателя (ВНП, национального дохода, производительности труда и т.п.); 2) разработка методологии подсчета и расчета статистического показателя. Система статистических показателей – совокупность статистических показателей, отражающая взаимосвязи, которые объективно существуют между явлениями. Система статистических показателей охватывает все стороны жизни общества на различных уровнях: − страны – макроуровень; − региона – мезоуровень; − предприятий, фирм, объединений, семей, домохозяйств – микроуровень. Более подробно статистические показатели будут рассмотрены в разделе 4.
СТАТИСТИЧЕСКОЕ НАБЛЮДЕНИЕ СТАТИСТИЧЕСКАЯ СВОДКА Предварительный контроль материалов Предварительный контроль включает логическую проверку данных, т.е. смысловую согласованность сведений, исключение «нелогичных» данных и арифметическую согласованность. Пример 3.1. Рассогласованные данные. При переписи населения в документах указан мальчик 8 лет, состоящий в браке. Пример 3.2. В документах на предприятии обнаружены арифметическая и логическая рассогласованность:
Арифметическая – неправильно определена сумма заработной платы. В 3-й строке имеется логическая ошибка: человек 25 лет не может иметь общего стажа 45 лет и, кроме того, непрерывный стаж, как часть общего, не может его превосходить.
В процессе сводки материалы упорядочиваются и делятся на группы по существенным признакам. Это достигается с помощью группировки. Вторичная группировка Иногда приходится пользоваться уже имеющимися группировками, которые не удовлетворяют требованиям анализа. Например, имеющиеся группировки могут быть несопоставимы из-за различного числа выделенных групп или неодинаковых границ интервалов. В этом случае используется метод вторичной группировки, являющейся особым видом группировки. Вторичная группировка – образование новых групп на основе ранее осуществленной группировки. Получение новых групп на основе имеющихся возможно двумя способами перегруппировки: объединением первоначальных интервалов (путем их укрупнения) и долевой перегруппировкой (на основе закрепления за каждой группой определенной доли единиц совокупности). Пример 3.4. Распределение акционеров двух районов области по размеру дивидендов на одну акцию в 2006 г.
Приведенные данные не позволяют сравнить распределение акционеров двух районов по размеру дивидендов на одну акцию, так как в районах имеется различное число групп акционеров, и различны величины интервалов. Необходимо ряды распределения привести к сопоставимому виду. За основу сравнения возьмем структуру распределения акционеров второго района (как наиболее крупную). Следовательно, по первому району нужно произвести вторичную группировку или перегруппировку акционеров, образовав такое же число групп и с теми же интервалами, как во втором районе. В результате перегруппировки получаем следующие сопоставимые данные.
Анализ данных вторичной группировки позволяет сделать вывод о том, что акционеры второго района имеют более высокие размеры дивидендов (120 тыс. руб. и более на одну акцию выплачивают 70% акционеров этого района, а в первом районе — только 30% акционеров).
СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ Абсолютные показатели Различают два вида абсолютных статистических величин: индивидуальные и суммарные. Индивидуальными называют абсолютные статистические величины, характеризующие размеры признака у отдельных единиц совокупности (например, размер заработной платы отдельного работника, вклада гражданина в определенном банке и т. д.). Суммарные –характеризуют численность совокупности или объем варьирующего признака. Абсолютные показатели представляют собой именованные числа, т. е. имеют какую-либо единицу измерения. В зависимости от сущности исследуемого социально-экономического явления абсолютные статистические величины выражаются в − натуральных (тонны, штуки, метры, литры), − стоимостных (рубли), − трудовых (человеко-днях, человеко-часах) единицах измерения. Абсолютные статистические величины могут быть положительными (доходы) и отрицательными (убытки, потери).
Относительные показатели Основные виды относительных величин чаще выражаются отвлеченными числами, но могут быть также именованными относительными показателями. Их построение связано с применением различных методов статистики. Относительные показатели можно подразделить на следующие группы. 1. Характеризующие структуру объекта. Это доля (удельный вес) - отношение части к целому. Например, отношение площади каждой из сельскохозяйственных культур к общей посевной площади; числа женщин к общей численности населения города, республики. Выражаются в процентах или промилле (тысячных долях). 2. Характеризующие динамику процесса, изменение во времени. Это отношения показателей, характеризующих объект в более позднее время (текущий период), к аналогичным показателям того же объекта в более ранний (базисный) период. Их называют темпами роста. Выражаются в разах или в процентах. 3. Характеризующие взаимосвязь признаков в совокупности явлений. Например, связь уровня душевого дохода с размером потребления мяса или фруктов на одного человека; связь дозы удобрений с урожайностью картофеля и т.п. К ним относятся коэффициенты корреляции, эластичности, детерминации, аналитические индексы. 4. Характеризующие соотношение разных признаков того же объекта между собой (иногда их называют показателями интенсивности). Например, производительность труда – отношение произведенной продукции в натуральном или стоимостном выражении к затратам труда на ее производство и др. Выражаются именованными числами с двойными единицами измерения обоих сравниваемых признаков: в рублях за 1 час труда, в центнерах с 1 га площади. 5. Отношения фактически наблюдаемых величин признака к его нормативным, плановым, оптимальным или максимально возможным, величинам. Это широко распространенные на производстве показатели выполнения норм выработки, норм расхода материалов и других ресурсов. Отношения наблюдаемых величин признака к оптимальным или плановым характеризуют приближение изучаемого процесса к идеалу. 6. Сравнения разных объектов по одинаковым признакам. Сравнение урожайности одной и той же культуры в том же году между хозяйствами, областями; сравнение показателей производства или уровня жизни населения в разных странах — это обычные приемы познания.
Статистические таблицы Статистическая таблица – система строк и столбцов, в которых в определенной последовательности и связи излагается статистическая информация о социально-экономических явлениях. В статистической таблице обязательно имеется заголовок, в котором должны быть указаны цель построения таблицы, территория и время, к которому относятся данные. Пишется жирным шрифтом. Если все единицы измерения одинаковы, то указываются они в заголовке таблицы. Если они разные – то в верхних или боковых заголовках таблицы. Разграфка таблицы должна включать как можно меньше линий – только горизонтальные линии, отделяющие таблицу от ее заголовка; заголовки граф от значений показателей; итоговую строку таблицы. Вертикальные линии могут присутствовать или отсутствовать. Заголовки граф содержат названия показателей (без сокращения слов), их единицы измерения. Иногда заголовки нумеруются. Жирный шрифт. Цифровые данные записываются с одной и той же степенью точности в пределах каждой графы. В таблице не должно быть ни одной пустой клетки: с таких случаях ставится знак «–». Размер шрифта заголовков граф и данных на 2 п. меньше, чем в основном тексте. Пример 5.1. Статистическая таблица Таблица 5.1. Распределение акционерных компаний n -го района по типам в 200_ г.
Статистические графики Статистический график – условное изображение числовых величин и их соотношений посредством линий, геометрических фигур, рисунков или географических карт-схем. Главное достоинство графиков – наглядность рассмотрения статистических данных. Основными элементами графиков, изображающих количественные соотношения, являются шкала, масштаб, оси координат и числовая (координатная) сетка. График должен иметь заглавие, отражающее содержание изображаемого явления, время и место, к которому относятся данные, и расшифровку условных обозначений. Заглавие пишется снизу графика. Для большей наглядности графика применяют различную штриховку, окраску и т. д. По способу построения графики делятся на диаграммы, картограммы, картодиаграммы. Диаграммы являются наиболее распространенными. Виды диаграмм: линейные, точечные, плоскостные, объемные, фигурные. Линейные графики используются для представления количественных переменных: − характеристики вариации их значений (оси: Y – значения признака, X – номер наблюдения), − полигон (оси: Y – частоты, X – значения признака, из первой и последней точек перпендикуляры на ось X), − кумулята (оси: Y – накопленные частоты или частости, X – значения признака), − огива (оси: Y – значения признака, X – накопленные частоты или частости), − кривая Лоренца (оси: Y – нарастающие доли значений признака в общем объеме, X – накопленные частости) строится для изучения концентрации какого-либо признака в тех или иных группах совокупности. − динамики (Y – значения признака, X – время) (рис. 5.1), − взаимосвязи между переменными (Y – значения зависимого признака, X – значения независимого признака: уравнение регрессии).
Рис. 5.1. Валовый региональный продукт Челябинской области, млн. руб.
Точечные диаграммы (поле корреляции) обычно используют для анализа взаимосвязи между переменными (Y – значения зависимого признака, X – значения независимого признака). Плоскостные диаграммы: − столбиковая (гистограмма): обычно для изображения интервального вариационного ряда (оси: Y – частоты или плотности, X – интервалы) (рис. 5.2), − ленточная (горизонтальная столбиковая), − секторная: применяется для иллюстрации структуры изучаемой совокупности (круг – 100%, сектора – части совокупности). Пример секторной диаграммы приведен на рис. 5.3. Гистограммы строятся наиболее часто.
Рис. 5.2. Численность населения города, тыс. чел.
Рис. 5.3. Структура промышленного производства в России в 2007 г.
Возможно одновременное построение плоскостных и линейных диаграмм (рис. 5.4).
Рис. 5.4. Объемы производства по городу и градообразующему предприятию за 1998-2003 гг., млн. руб.
Объемные диаграммы строятся аналогично плоскостным диаграммам только в виде объемных столбиков и секторов. Фигурные диаграммы усиливают наглядность изображения, так как включают рисунок изображаемого показателя. Площадь фигуры соответствует величине показателя. Картограмма применяется для изображения географической характеристики изучаемых явлений. Она показывает размещение изучаемого явления, его интенсивность на определенной территории – республике, области, районе. Картограммы бывают фоновые и точечные. Картодиаграмма – сочетание диаграммы с географической картой. Используются различные фигуры, которые размещаются на контуре географической карты. В настоящее время пространственное представление статистических данных используется все шире. Например, представление в электронном виде карты районов города с обозначением социальных учреждений, проживания категорий граждан, фиксация случаев пожара, правонарушений и т.д.
Понятие средней величины Средняя величина – обобщающая количественная характеристика однородной совокупности явлений по определенному признаку. Характеризует величину изучаемого признака, приходящуюся на единицу совокупности. Признак, по которому находится среднее, называется усредняемое. Величина усредняемого признака у каждой единицы совокупности – индивидуальное значение. Метод средних величин заключается в замене индивидуальных значений варьирующего признака единиц наблюдения (x1, x2,…,xn) некоторой уравненной величиной Средняя величина должна быть рассчитываема для количественно-однородной совокупности. Это требование состоит в том, что среднее нельзя применить к таким совокупностям, отдельные части которых подчинены различным законам развития величин признака. Средняя гармоническая Рассчитывается, когда изучаемые показатели связаны между собой как x и1/ x (показатели на единицу времени, сырья и т.д.). Средняя гармоническая простая: Пример 6.4. Требуется вычислить среднюю производительность труда бригады из 3-х человек, если первому рабочему требуется для изготовления одной детали 1/4 часа, второму - 1/3 часа, третьему - 1/2 часа.
Средняя гармоническая взвешенная: Средняя геометрическая Применяется, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин.
Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста. Пример 6.5. В результате инфляции за первый год цена товара возросла в 2 раза к предыдущему году, а за 2-й год еще в 3 раза к уровню предыдущего года. Т.е. за 2 года цена выросла в 6 раз. Какой средний темп роста цены за год? Если считать по средней арифметической, то Средняя геометрическая дает правильный ответ: Средняя квадратическая Применяется, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин. Средняя квадратическая простая:
Пример 6.6. Имеется 3 участка земельной площади со сторонами квадрата: x1 = 100 м; x2 = 200 м; x3 = 300 м. Чему равна средняя площадь участков? Общая площадь участков равна (100)2 + (200)2 + (300)2 = 140000 м2. Если считать по средней арифметической, то Средняя квадратическая дает правильный ответ:
Средняя квадратическая взвешенная:
Средняя степенная Обобщает все виды средних
Если k = -1, то это средняя гармоническая, k = 0 – средняя геометрическая (после преобразований), k = 1 – средняя арифметическая, k = 2 – средняя квадратическая, k = 3 – средняя кубическая. Имеется следующее соотношение между формами средних величин:
или
Пользуясь этим правилом статистика может управлять средними. Пример 6.7. Студент на экзамене получил за 1-й вопрос оценку 2, за 2-ой вопрос – 5.
Исходя из полученных средних можно как «завалить» студента, так и «вытянуть». Структурные характеристики Если величина средней зависит от всех значений признака, встречаемых в данном распределении, то значение средней определяется структурой распределения, местом распределения. Медиана – значение признака, приходящееся на середину ранжированной совокупности. Медиана делит совокупность на две равные части. Пример 6.8. Вес 7 телят: 75, 80, 83, 87, 92, 97, 101 кг. Медиана равна 87 кг (половина телят имеет вес меньше 87 кг, а половина – больше 87 кг). Вес 8 телят: 75, 80, 83, 87, 92, 97, 101, 105 кг. Медиана равна (87+92)/2=89,5 кг.
Медиана в интервальном ряду рассчитывается следующим образом: Сначала исчисляют порядковый номер медианы по формуле Накопленной частоте, которая равна порядковому номеру медианы или первая его превышает, соответствует медианный интервал. Медиана равна:
где x0 – нижняя граница медианного интервала; h – величина медианного интервала; fi – частота i-го интервала; Sме-1 – сумма накопленных частот в интервале, предшествующем медианному; fMe – частота медианного интервала. Пример 6.9. Имеются данные о заработной плате рабочих:
Квартили – значения признака, делящие ранжированную совокупность на четыре равные по числу единиц части. Номер квартильного интервала рассчитывается аналогично медианному в соотношении ¼ к совокупности. 1-й квартиль равен:
xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%), h – величина интервала, fQ1 – частота квартильного интервала, SQ1-1 – сумма накопленных частот в интервале, предшествующего квартильному. 2-й квартиль: Q2=Мe. 3-й квартиль:
обозначения аналогичны 1-му квартилю с изменением на номер интервала. Пример 6.10. По данным примера 6.9.
Децили – значения признака, делящие ранжированную совокупность на десять равных по числу единиц частей. Вычисляются они по той же схеме, что и медиана, и квартили. Обычно рассчитывают только первый и девятый децили:
Пример 6.11. По данным примера 6.9.
Децильный коэффициент Пример 6.12. По данным примера 6.11.
Мода – значение признака, которое чаще других встречается в изучаемом ряду распределения. Мода для дискретного ряда определяется как варианта, имеющая наибольшую частоту. Для интервального ряда:
где x0 –нижняя граница модального интервала, d - величина модального интервала, fMo-1 - частота интервала, предшествующего модальному, fMo - частота модального интервала, fMo+1 - частота интервала, следующего за модальным. Пример 6.13. По данным примера 6.9. Модальный интервал с наибольшей частотой fi = 4 равен 1000-1200.
Показатели размера вариации Вариация – изменение значения признака при переходе от одной единицы совокупности к другой. Для измерения вариации используются следующие показатели. 1. Размах вариации – показывает, в каких пределах колеблется размер признака, образующего ряд распределения R=xmax-xmin, где xmax – максимальное значение признака, xmin – минимальное значение признака. 2. Среднее линейное отклонение – показывает, на сколько в среднем отклоняются значения признака от его среднего значения. По несгруппированным данным
По сгруппированным данным
где k – число групп. 3. Дисперсия – средний квадрат отклонений индивидуальных значений признака от их средней величины. По несгруппированным данным
По сгруппированным данным
Дисперсия имеет большое значение в статистическом анализе. Однако ее не всегда удобно использовать, потому что размерность дисперсии равна квадрату размерности изучаемого признака. Поэтому рассчитывают среднее квадратическое отклонение. 4. Среднее квадратическое отклонение – показывает, на сколько в среднем отклоняются значения признака от его среднего значения (обладает лучшими свойствами, чем среднее линейное отклонение). По несгруппированным данным
По сгруппированным данным
Выражается в тех же единицах измерения, что и признак. 5.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 463; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.80.194 (0.011 с.) |





 .
. .
.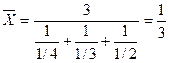 часа.
часа. .
. .
.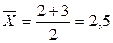 раза, тогда за два года выросла бы в 2,5 · 2,5 = 6,25 раза, а не в 6 раз.
раза, тогда за два года выросла бы в 2,5 · 2,5 = 6,25 раза, а не в 6 раз. раза.
раза. .
. м2, тогда общая площадь равна 3 · (200)2 = 120000 м2, что неверно.
м2, тогда общая площадь равна 3 · (200)2 = 120000 м2, что неверно. м2.
м2.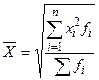 .
. .
.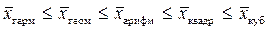
 .
. балла.
балла. балла.
балла. балла.
балла. и строят ряд накопленных частот Si=fi+Si-1 (S1=f1).
и строят ряд накопленных частот Si=fi+Si-1 (S1=f1). ,
, , следовательно, медианный интервал 1000-1200.
, следовательно, медианный интервал 1000-1200. $ (половина рабочих имеет заработную плату ниже 1050$, а половина – выше 1050$).
$ (половина рабочих имеет заработную плату ниже 1050$, а половина – выше 1050$).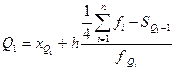 ,
, ,
,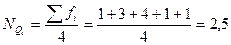 , следовательно, 1-й квартильный интервал 800-1000.
, следовательно, 1-й квартильный интервал 800-1000. $ (25% рабочих получает заработную плату ниже 900$).
$ (25% рабочих получает заработную плату ниже 900$). , следовательно, 3-й квартильный интервал 1000-1200.
, следовательно, 3-й квартильный интервал 1000-1200. $ (25% рабочих получает заработную плату выше 1175$).
$ (25% рабочих получает заработную плату выше 1175$). ,
, .
. , следовательно, 1-й децильный интервал до 800.
, следовательно, 1-й децильный интервал до 800. $ (10% рабочих получает заработную плату ниже 800$).
$ (10% рабочих получает заработную плату ниже 800$). , следовательно, 9-й децильный интервал 1200-1400.
, следовательно, 9-й децильный интервал 1200-1400.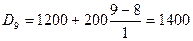 $ (10% рабочих получает заработную плату выше 1400$).
$ (10% рабочих получает заработную плату выше 1400$). . Широко применяется при изучении дифференциации доходов.
. Широко применяется при изучении дифференциации доходов.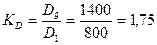 (10% самых высокооплачиваемых работников получают зарплату в 1,75 раза больше 10% самых низкооплачиваемых работников).
(10% самых высокооплачиваемых работников получают зарплату в 1,75 раза больше 10% самых низкооплачиваемых работников). ,
, $ (наибольшее число рабочих получает зарплату 1050$).
$ (наибольшее число рабочих получает зарплату 1050$). .
. ,
,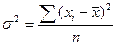 .
. .
.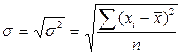 .
. .
.


