
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели взаимосвязи количественных переменныхСодержание книги
Поиск на нашем сайте
Для ориентировочной оценки тесноты связи между двумя статистическими показателями используются следующие коэффициенты. Коэффициент корреляции знаков Фехнера (i) Определяется сопоставлением знаков отклонений x и y от их средних и подсчетом числа случаев совпадения и несовпадения знаков.
где u – число пар с одинаковыми знаками отклонений от средних, v – число пар с разными знаками отклонений от средних. -1 < i < +1. Если i близок к +1, то – тесная прямая связь. Если i близок к -1, то – тесная обратная связь. Если i близок к 0, то – связи нет. Коэффициент корреляции рангов Спирмена (ρ)
где n – число рангов, Rx – ранг показателя x, Ry – ранг показателя y. Если среди значений рангов по уровням встречаются одинаковые, то образуются одинаковые средние номера. Например, вместо одинаковых по порядку третьего и четвертого значений ряда будут два ранга по 3,5. Если ρ близок к +1, то – тесная прямая связь. Если ρ близок к -1, то – тесная обратная связь. Если ρ близок к 0, то – связи нет. Линейный коэффициент корреляции (rxy)
где σx и σy – среднее квадратическое отклонение x и y соответственно. -1 < rxy < +1. Если | rxy |≥0,7 – связь сильная, если 0,5≥| rxy |<0,7 – связь средняя, если | rxy |<0,5 – связь слабая. При сильной и средней связи, если rxy >0, то связь прямая, иначе – обратная. Пример 11.1. Зависимость между затратами производства (X, тыс. руб.) и прибылью (Y, тыс. руб.) 10 малых предприятий района за неделю характеризуется следующими данными.
Определить тесноту связи между затратами производства и прибылью малых предприятий.
u =8, v =2.
Следовательно, связь между затратами производства и прибылью малых предприятий района сильная и прямая. Определение параметров парной линейной регрессии Наиболее простой случай корреляционной зависимости является парная корреляция – зависимость между двумя признаками (y и x). Уравнение такой связи называется парной линейной регрессией:
где y – зависимая переменная, x – факторный признак, α – свободный коэффициент уравнения, β – коэффициент регрессии: показывает, на сколько изменится среднее значение y ( Графическое представление парной линейной регрессии. Парная регрессия легко определяется по графическому изображению реальных статистических данных в виде точек (корреляционное поле или диаграмма рассеивания).
Рис. 11.1. Графическое представление линии парной регрессии с МНК-параметрами
Метод наименьших квадратов. Параметры α и β рассчитываются методом наименьших квадратов (МНК) по данным об n значениях признаков x и y. Исходное условие МНК для парной регрессии имеет вид:
То есть МНК позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений зависимой переменной y от расчетных (теоретических) минимальна. Чтобы найти минимум этой функции необходимо вычислить производные по каждому из параметров α и β и приравнять их к нулю:
Если первое уравнение разделить на n, то получится:
Решая систему уравнений далее, находится коэффициент регрессии β:
где
Пример 11.2. По данным примера 11.1. определить параметры и построить график уравнения парной линейной регрессии, определить тесноту связи с помощью парного коэффициента корреляции.
Тогда уравнение регрессии будет
Рис. 11.2. Уравнение парной регрессии и фактические данные
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.42.13 (0.009 с.) |

 ,
, ,
, ,
,

 ,
,  ,
, – связь средняя прямая.
– связь средняя прямая. – связь тесная прямая.
– связь тесная прямая.
 ,
, ) при увеличении x на единицу.
) при увеличении x на единицу.

 Þ
Þ 
 Þ
Þ 

 - среднее значение x,
- среднее значение x, 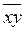 - среднее значение произведения xy,
- среднее значение произведения xy,  - дисперсия показателя x.
- дисперсия показателя x. ,
,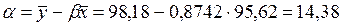
 .
.



