
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ основной тенденции в рядах динамикиСодержание книги
Поиск на нашем сайте
Описание тенденции в ряду динамики производится на основе выявления типа уравнения тренда, выражающего качественные свойства развития. Основные формы тренда. 1. Линейный
где y – уровни ряда динамики, t – моменты или периоды времени, а – начальный уровень тренда в момент или период, принятый за начало отсчета времени t, b – среднегодовой абсолютный прирост. Пример, тенденции динамики урожайности для больших территорий (область, край, республика, страна). 2. Параболический
где с – половина ускорения. Выражает ускоренное или замедленное изменение уровней ряда с постоянным ускорением. Возможно нахождение максимума или минимума. Например, население города (тыс. чел) возрастает по параболе
Производная по t будет иметь вид: 60 - 4t = 0, откуда t=15. Максимум населения будет достигнут через 15 лет после начала отсчета времени. В начальный момент времени население составляло 1100 тыс. чел. Максимум будет равен
3. Экспоненциальный
где a – константа, k – темп изменения в разах. Если k>1, то выражает тенденцию ускоренного и все более ускоряющегося возрастания уровней ряда. Например, рост вирусных заболеваний при отсутствии борьбы с ними. Может продолжаться небольшой период, поскольку всегда возникнут ограничения. Если k<1, то выражает тенденцию постоянно все более замедляющегося снижения уровней ряда. Например, динамика трудоемкости продукции при технологическом прогрессе. 4. Логарифмический
Отображает тенденцию замедляющегося роста уровней при отсутствии предельно возможного значения. Например, динамика роста спортивных достижений, повышение продуктивности скота.
Выявить тип тренда возможно графическим методом, путем построения графика зависимости y от t. Если наглядно по исходным данным выявить тренд невозможно, то осуществляется сглаживание уровней ряда методом скользящей средней. Метод скользящей средней: 1. Определяется интервал сглаживания, т.е. число входящих в него уровней m (2, 3, 5, 7 и т.д.). 2. Вычисляется среднее значение уровней, образующих интервал сглаживания, по формуле
где m – число уровней, входящих в интервал сглаживания, i – порядковый номер уровня в интервале сглаживания, p – при нечетном m равно: p=(m-1)/2. При четном m проводят центрирование: находят среднюю из двух смежных скользящих средних для отнесения полученного уровня к определенной дате.
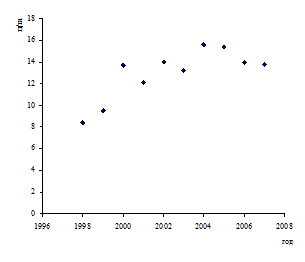
3. Сдвинуть интервал сглаживания на одну точку вправо, затем вычислить все последующие сглаженные значения, производя одновременно сдвиги. Пример 8.4. Определить тип тренда на основе данных по урожайности за период 1998-2007 гг.
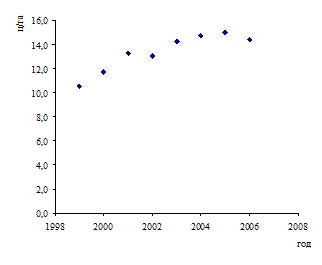
Рис. 9.1. Динамика урожайности до и после сглаживания
До сглаживания возможны линейный, параболический и логарифмический тренды. После сглаживания – линейный.
Измерение устойчивости в динамике По отношению к статистическому изучению динамики рассматривается два аспекта устойчивости: 1) как категория противоположная колеблемости, 2) как устойчивость тенденции. 1) Коэффициент устойчивости
где σ – среднеквадратическое отклонение
2) Коэффициент корреляции рангов Ч. Спирмена ρ.
где n – число уровней, Rt – ранг лет, Ry – ранг уровней. Если среди значений рангов по уровням встречаются одинаковые, то образуются одинаковые средние номера. Например, вместо одинаковых по порядку третьего и четвертого значений ряда будут два ранга по 3,5. Если ρ близок к +1, то – высокая устойчивость возрастания уровней. Если ρ близок к -1, то – высокая устойчивость снижения уровней. Если ρ близок к 0, то – неустойчивость тенденции. Пример 8.5. Определить устойчивость тенденции урожайности по данным примера 8.4.
Так как ρ близок к +1, то устойчивость тенденции урожайности достаточно высокая.
ИНДЕКСЫ Понятие и виды индексов Индекс – относительная величина, характеризующая изменение социально-экономического явления во времени, пространстве и по сравнению с планом. Индексы позволяют решить следующие задачи: 1. определить средние изменения сложных, непосредственно несоизмеримых совокупностей во времени – индексы как показатели динамики; 2. оценить среднюю степень выполнения плана по совокупности в целом или ее части – индексы как показатели выполнения плана; 3. установить средние соотношения сложных явлений в пространстве – индексы как показатели сравнения; 4. определить роль отдельных факторов в общем изменении сложных явлений во времени или пространстве и, в частности, изучить структурные сдвиги – индексы как аналитические показатели. По степени охвата индексы различают − индивидуальные (i); − общие (I): агрегатные и средневзвешенные. Каждый индекс включает два вида данных: − оцениваемые (отчетные): обозначаются значком «1»; − база сравнения (базисные): обозначаются значком «0». Индивидуальные индексы Индивидуальный индекс (i) – выражает соотношение отдельных элементов совокупности. Принятые обозначения: q – физический объём, p – цена, z – себестоимость, t – затраты времени на производство единицы продукции. Следовательно, pq – стоимость продукции или товарооборот, zq – издержки производства. Индекс физического объёма продукции:
где q0 – количество произведенной продукции в базисный период, q1 – количество произведенной продукции в текущий период. Индекс цены:
Индекс себестоимости:
Индекс трудоемкости:
По базе сравнения различают − базисный индекс – если в качестве базы для сравнения принят один и тот же начальный уровень; − цепной индекс – если в качестве базы для сравнения принят уровень предыдущего периода. Если базисные и цепные индексы охватывают один и тот же период, между ними существует определенная взаимосвязь: произведение цепных индексов равно базисному. Индекс произведения равен произведению индексов сомножителей. Например, индекс товарооборота:
Такие индексы называются сопряженными, так как их взаимосвязь дает возможность по двум имеющимся индексам находить третий.
Агрегатные индексы Общий индекс – показывает соотношение совокупности явлений, состоящей из разнородных, непосредственно несоизмеримых элементов. Основной формой общего индекса является агрегатный индекс. Для того, чтобы его построить необходимо свести различные элементы сложного явления к такому виду, который делает их соизмеримыми. Индекс физического объёма продукции (Ласпейреса, 1864 г.)
Индекс физического объёма продукции (Г. Паше, 1874 г.)
Индекс цены (Ласпейреса)
Индекс цены (Пааше)
Индекс товарооборота
Индекс издержек производства
Та часть индекса, которая не изменяется называется весом. Веса свободного индекса в агрегатной форме выбираются исходя из следующих данных: − если индексируемая величина – количественный показатель, то вес выбирается на уровне базисного периода. − если индексируется величина – качественный признак вес принимается на уровне текущего периода.
Пример 9.1. Имеются данные о производстве сельскохозяйственным предприятием продукции за 2006 и 2007 гг.
Индекс товарооборота:
Это значит товарооборот текущего периода по отношению к базисному вырос на 7% этот показатель отражает изменение товарооборота под влиянием р и q. Индекс физического объёма продукции (Ласпейреса):
Это значит товарооборот в текущем периоде возрос на 17 % в связи с изменением объёма реализации.
Индекс цены (Пааше):
Индекс цены показал нам, что стоимость продукции в текущем периоде по сравнению с базисным сократился на 9% под влиянием изменения цен. Средневзвешенные индексы В случае если мы располагаем значениями индивидуальных индексов и произведениями pq, то агрегатные индексы преобразовывают в среднеарифметический и среднегармонический индексы. В случае, когда не известны отдельные значения p1 и q1, а дано произведение p1q1 – товарооборот отчетного периода и индивидуальные индексы цен ip, и агрегатный индекс должен быть вычислен с отчетными весами (по Пааше), то применяется среднегармонический индекс цены:
В случае, когда не известны отдельные значения p0 и q0, а дано произведение p0q0 – товарооборот базисного периода и индивидуальные индексы физического объема iq, и агрегатный индекс должен быть вычислен с базисными весами (по Ласпейресу), то применяется среднеарифметический индекс физического объема:
Пример 9.2. Рассчитать средневзвешенные индексы по данным примера 9.1.
Индексы средней величины При изучении качественных показателей часто приходится рассматривать изменение средней величины индексируемого показателя для определенной однородной совокупности. Например, в статистических сборниках публикуются данные о динамике средних цен на определенные продукты, средней урожайности зерновых культур, средней номинальной заработной плате в отдельных отраслях экономики и т.д. Средняя величина формируется под влиянием индивидуальных значений самого показателя и соотношения их весов («структуры объекта»). Выделяют три индекса средней величины. 1. Индекс переменного состава
где x – значение качественного индексируемого показателя, f – вес x, нижний индекс «1» - значения показателя в отчетном периоде, нижний индекс «0» - значения показателя в базисном периоде,
Индекс переменного состава отражает динамику среднего показателя за счет изменения x у отдельных элементов и за счет изменения состава совокупности. 2. Индекс фиксированного (постоянного) состава
Он отражает динамику среднего показателя только за счет изменения x, при фиксировании состава, как правило, на уровне отчетного периода. 3. Индекс структурных сдвигов
Он отражает динамику среднего показателя только за счет изменения структуры при фиксировании x на уровне базисного периода.
Заметим, что между рассмотренными индексами существует взаимосвязь:
следовательно, зная два индекса можно рассчитать третий. Рассмотрим применение индексов средней величины на примере индекса цен. Средняя цена определяется как
где pi – цена товара на i -м рынке, Индекс переменного состава: Индекс фиксированного состава: Индекс структуры: Пример 9.3. На трех рынках города продается картофель. Данные о продаже за день в зарегистрированных ценах приведены в таблице.
Средняя цена в августе: Средняя цена в сентябре: Наибольшее снижение цен произошло на Старом рынке. Наибольшее увеличение объема продаж – на Новом рынке, в результате чего доля этого рынка по объемам продаж составила почти половину всего объема.
то есть средняя цена по трем рынкам города снизилась на 4,22%.
то есть среднее снижение цен на рынках было 4,63%. Различие между индексами переменного и постоянного состава вызвано изменением структуры продаж:
или
то есть за счет изменения структуры продаж средняя цена картофеля возросла на 0,43% или на 8 коп/кг (17,34-17,26). Это связано с повышением удельного веса Нового рынка, на котором цены выше.
Аналогично рассмотрим индексы средней величины для себестоимости продукции. Индекс переменного состава: Индекс фиксированного состава: Индекс структуры:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.155.143 (0.012 с.) |

 ,
, ,
, .
.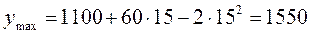 тыс. чел.
тыс. чел. ,
, .
. ,
,
 ,
, ,
, 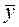 - средний уровень ряда, n – число уровней.
- средний уровень ряда, n – число уровней. ,
,
 ц.га.
ц.га. ,
,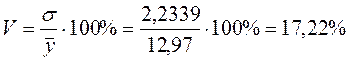 . Колеблемость уровней ряда относительно среднего уровня составляет 17,22%, следовательно, устойчивость ряда динамики высокая.
. Колеблемость уровней ряда относительно среднего уровня составляет 17,22%, следовательно, устойчивость ряда динамики высокая.
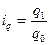 ,
, .
.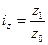 .
. .
. .
. .
. .
. .
.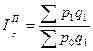 .
.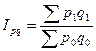 .
. .
.
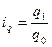



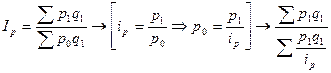 .
. .
. ,
, .
. ,
, .
. .
. ,
, ,
, - структура продаж.
- структура продаж.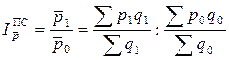 .
. .
. .
. руб./кг.
руб./кг. руб./кг.
руб./кг. или 95,78%,
или 95,78%,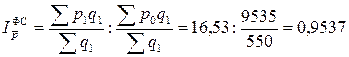 или 95,37%,
или 95,37%,
 ,
, .
. .
. .
.


