Показатели асимметрии и эксцесса распределения

Распределение случайной величины x называют нормальным , если соответствующая ей плотность распределения равна

.

Коэффициент асимметрии – характеризует степень асимметричности распределения. Предложен английским статистиком К. Пирсоном.

.

Если As < 0, то левосторонняя асимметрия,

если As > 0, то правосторонняя асимметрия (рис. 6.1).

 

Рис. 6.1. Асимметрия распределения: а – левосторонняя, б – правосторонняя

 

Эксцесс – характеризует наличие в изучаемой совокупности слабо варьирующего по данному признаку «ядра», окруженного рассеянным «гало».

Показатель эксцесса рассчитывается по формуле:

для несгруппированных данных

,

для сгруппированных данных

.

Если Ex < 3, то «ядра» нет, если Ex > 3, то «ядро» есть (рис. 6.2).

Рис. 6.2. Эксцесс распределения

 

ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ

Понятие и причины использования выборочного метода

Выборочное наблюдение – способ несплошного наблюдения, при котором обследуется не вся совокупность, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение дан­ных, характеризующих всю совокупность в целом.

Причины использования выборочного метода:

1. Повышение точности данных. Уменьшение числа единиц наблюдения в выборке резко снижает ошибки регистрации, но увеличивает ошибку репрезентативности. Однако качество данных можно повысить, привлекая более квалифицированных исполнителей.

2. Экономия материальных, трудовых, финансовых ресурсов и времени.

3. Порча наблюдаемых объектов. Например, изучение качества продукции: проверка молока на жирность, электрических ламп на длительность горения.

 

Виды и схемы отбора

Размер ошибки выборки и методы ее определения зависят от вида и схемы отбора.

Различают четыре вида отбора совокупности единиц наблюдения:

1. случайный;

2. механический;

3. типический;

4. серийный (гнездовой).

Случайный отбор. В случай­ном порядке отбирается необходимое количество единиц совокупнос­ти. Каждая из единиц имеет одинаковую вероятность попасть в выборку. Наиболее распространенный вид отбора.

Пример 7.1. Тиражи выигрышей: из общего количества выпущенных билетов в случайном поряд­ке наугад отбирается определенная часть номеров, на которые прихо­дятся выигрыши. При этом всем номерам обеспечивается равная воз­можность попасть в выборку.

Механический отбор. Все единицы изучаемой совокупности предварительно располагаются в определенном порядке – например, по алфавиту, местоположению и т. п., а потом, в зависимости от объ­ема выборки, механически, через определенный интервал, отбирается необходимое количество единиц.

Пример 7.2. 10%-ная ме­ханическая выборка студентов. Составляется список их фамилий по алфавиту и механически отбирается каждый десятый студент, напри­мер: 1-й, 11-й, 21-й, 31-й или 7-й, 17-й, 27-й, 37-й и т. д. Если выборка 5%-ная, то отбирается каждый 20-й студент, т.е. интервал зависит от объема выборки. Чем меньше выборка, тем больше интервал.

Типический отбор. Изучаемая совокупность разбивается по су­щественному, типическому признаку на качественно однородные, од­нотипные группы. Затем из каждой группы случайным способом отби­рается количество единиц, пропорциональное удельному весу группы во всей совокупности.

Пример 7.3. Типический отбор 1500 студентов из 10000, обучающихся на четырех факультетах института. Для этого их группируют в однородные группы по факультетам, а затем по каж­дой из них отбирают число студентов пропорционально удельному весу числа студентов института по факультетам.

Типический отбор дает более точные результаты, чем случайный или механический, потому что при нем в выборку в такой же пропор­ции, как и в генеральной совокупности, попадают представители всех типических групп.

Серийный (гнездовой) отбор. Отбору подлежат не отдельные еди­ницы совокупности, а целые группы (серии, гнезда), отобранные слу­чайным или механическим способом. В каждой такой группе, серии проводится сплошное наблюдение, а результаты переносятся на всю совокупность.

Пример 7.4. 10 тыс. студентов института занимаются группами по 25 человек. Для проведения 15%-ного выборочного наблюдения се­рийным (гнездовым) способом необходимо в случайном порядке ото­брать 60 групп (1500/25 = 60) из 400 (10 000/25 = 400) и результаты наблюдения перенести на всю совокупность.

Выборка проводится по схеме повторного или бесповторного отбора.

Повторный отбор. Каждая отобранная единица или серия воз­вращается во всю совокупность и может вновь попасть в выборку. Так называемая схема возвращенного шара.

Бесповторный отбор. Каждая обследованная единица изымается и не возвращается в совокупность, поэтому она не попадает в повторное обследование. Схема невозвращенного шара.

Бесповторный отбор дает более точные результаты по сравнению с повторным, так как при одном и том же объеме выборки наблюдение охватывает большее количество единиц изучаемой совокупности.

В социально-экономической статистике нет смысла применять повторную выборку, поэтому, как правило проводится бесповторный отбор.

Основные характеристики параметров генеральной и выборочной совокупностей обозначаются символами:

Показатели	Генеральная совокупность	Выборочная совокупность
Объем совокупности	N	n
Средняя величина
Доля	p	w
Дисперсия

 

Ошибка выборки

Научным обоснованием случайных ошибок выборки являются тео­рия вероятностей и ее предельные теоремы. Применительно к выбороч­ному наблюдению пользуются теоремами русских математиков П.Л.Чебышева и A.M. Лягунова. Согласно этим теоремам с увеличением чис­ленности выборки размеры случайных ошибок сокращаются.

Различают сред­нюю и предельную ошибку выборки.

Средняя ошибка – такое расхождение между средними выборочной и генеральной совокупнос­тями (), которое не превышает .

Средняя ошибка выборочной средней равна

,

где σ – среднее квадратическое отклонение признака, n – объем выборочной совокупности.

Доказано, что между и есть следующее соотношение

или

.

Предельная ошибка – максимально возможное расхождение этих средних, т.е. мак­симум ошибки при заданной вероятности ее появления.

Предельная ошибка выборочной средней равна

,

где t – нормированное отклонение, определяется по таблицам t-критерия Стьюдента исходя из числа наблюдений (n) и доверительной вероятности (90%, 95%, 99%).

При числе наблюдений более 200 для доверительной вероятности 90% t =1,645; 95% - 1,96; 99% - 2,576.

Отсюда предельные значения генеральной средней определяются как

.

Это означает, что с заданной вероятностью значение генеральной средней будет находиться указанных в пределах.

Пример 7.5. Для определения скорости расчетов с кредиторами предприятия была проведена случайная выборка 50 платежных документов, по которым средний срок перечисления денег оказался равен 28,2 дня со стандартным отклонением 5,4 дня. Определить средний срок прохождения всех платежей в течение данного года с доверительной вероятностью 0,95.

Скорректированная дисперсия равна

.

Средняя ошибка выборочной средней равна

дня.

Значение нормированного отклонения для доверительной вероятности 0,95 равно 1,96. Тогда, предельная ошибка выборочной средней равна

дня.

Предельные значения X

дня.

Таким образом, с вероятностью 95% средняя продолжительность расчетов предприятия с кредиторами составляет не менее 26,69 дня и не более 29,71 дня.

 

Ошибка выборки для выборочной относительной величины (доли) определяется аналогично. Дисперсия относительной величины

,

где p – доля тех или иных единиц в выборке.

Среде значение переменной

.

Средняя ошибка выборочной доли

Предельная ошибка выборочной доли

.

Пример 7.6. По данным выборочного изучения 100 платежных документов предприятия оказалось, что в шести случаях сроки расчетов с кредиторами были превышены. Требуется установить доверительный интервал доли платежных документов предприятия без нарушения сроков с вероятностью 0,95.

Доля документов без нарушения сроков

.

Средняя ошибка выборочной доли

.

Предельная ошибка выборочной доли

.

Доверительный интервал

или .

 

Определение объема выборки

Объем выборки рассчитывается на стадии проектирования выборочного обследования. Для повторного отбора объем выборки равен

,

где Δ – допустимая погрешность, которая задается исследователем исходя из требуемой точности результатов проектируемой выборки;

t – табличное значение нормированного отклонения (определяется по таблицам t-критерия Стьюдента);

σ² – генеральная дисперсия.

Генеральная дисперсия как правило неизвестна, поэтому ее оценивают следующим образом. Если известно примерное значение средней величины, то

.

Если известны x_max и x_min, то в соответствии с правилом «трех сигм»

.

Если распределение заведомо ассиметричное, то

.

Для относительной величины считают максимальную величину дисперсии

.

Для бесповторного отбора объем выборки равен

,

где .

При больших размерах генеральной совокупности n незначительно отличается от n₀.

Пример 7.7. Для изучения структуры и стоимости покупок в универмаге из 10000 покупателей следует отобрать то число человек, которое бы обеспечивало с вероятностью 0,99 (t=2,576) определение средней стоимости покупок с точностью не менее 50 руб. По прошлому обследованию дисперсия равна 62500.

человек,

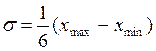человек.