Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По выполнению практических и лабораторных работСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ ЧАСТЬ II Учебно-методическое пособие По выполнению практических и лабораторных работ
Издание стереотипное
Великий Новгород
Рецензент доктор физико-математических наук, профессор Т.Г. Сукачева
Учебно-методическое пособие содержит поэтапную характеристику выполнения практических и лабораторных работ вручную и с использованием MS Excel и ППП Statistica, примеры и решения, задачи для самостоятельной работы студентов экономических специальностей Учебно-методическое пособие предназначено для студентов дневной и заочной форм обучения.
ББК 60.6 © Новгородский государственный университет, 2011 © Н.И. Гришакина, Г.В. Фетисова, О.Д. Притула, Д.П. Воронова составление, 2011 СОДЕРЖАНИЕ
ВВЕДЕНИЕ Учебно-методическое пособие по выполнению практических и лабораторных работ по статистике содержит требования по их выполнению, порядок расчетов вручную и с использованием MS Excel, Statistica. Часть II учебно-методического пособия характеризует расчет показателей вариации: размаха вариации, квартилей и квартильного отклонения, среднего линейного отклонения, дисперсии и среднего квадратического отклонения, коэффициентов осцилляции, вариации, асимметрии, эксцесса и других. Расчет показателей вариации наряду с построением интервальных и дискретных вариационных рядов и расчетом средних величин, представленными в части I пособия, имеет большое значение для анализа рядов распределения. В учебно-методическом пособии приводятся решения большого количества типовых задач, ярко иллюстрирующих основные положения изучаемых методов, содержатся: поэтапная характеристика выполнения практических и лабораторных работ с использованием ППП, задания для самостоятельного выполнения по вариантам, список рекомендуемой литературы по каждой теме. Пособие снабжено кратким словарем основных понятий, контрольными вопросами, тестовыми заданиями что дает возможность легкого усвоения материала. ПРАКТИЧЕСКАЯ РАБОТА 3 РАСЧЕТ ПОКАЗАТЕЛЕЙ ВАРИАЦИИ Цель работы: получение практических навыков в расчете различных показателей (меры) вариации в зависимости от поставленных исследованием задач. Порядок выполнения работы: 1. Определить вид и форму (простая или взвешенная) показателей вариации. 2. Рассчитать показатели степени вариации для сгруппированных и несгруппированных данных и показатели формы распределения. 3. Сформулировать выводы.
Пример расчета показателей вариации 1. Определение вида и формы показателей вариации.
Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным относятся: размах вариации, квартильное отклонение, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Относительными показателями являются коэффициенты осцилляции, вариации, относительное линейное отклонение, относительный показатель квартильной вариации и т. д. Размах вариации (R) является наиболее простым измерителем вариации признака и определяется по следующей формуле:
где
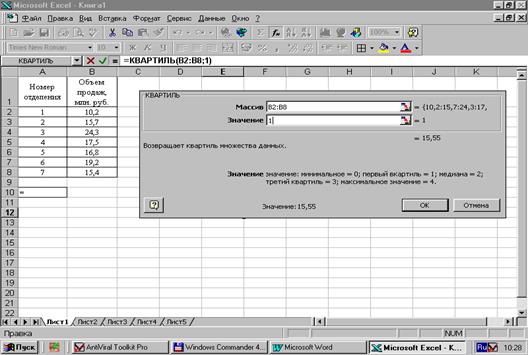
Квартильное отклонение (Q) – применяется для характеристики вариации признака в совокупности. Может использоваться вместо размаха вариации во избежание недостатков, связанных с использованием крайних значений.
где Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Квартили 1 и 3 определяются по формулам:
Причем
где Ме – медиана ряда;
условные обозначения те же, что и для величин В симметричных или умеренно асимметричных распределениях Q»2/3s. Так как на квартильное отклонение не влияют отклонения всех значений признака, то его использование следует ограничить случаями, когда определение среднего квадратического отклонения затруднительно или невозможно.
Среднее линейное отклонение (
Дисперсия (
Среднее квадратическое отклонение (s) – наиболее распространенный показатель вариации, представляет собой квадратный корень из значения дисперсии.
Пример 1. Таблица 1 Пример 2.
Таблица 4 Данные о товарообороте предприятий одной из отраслей промышленности.
Определить средний объем товарооборота, структурные средние, абсолютные и относительные показатели вариации и насколько фактическое распределение согласуется с нормальным (по показателям формы распределения). Для расчета показателей построим вспомогательную таблицу.
Таблица 5 Расчетная таблица
Размах вариации:
Среднее значение находим по формуле средней арифметической взвешенной:
В равноинтервальных рядах распределения мода (Mo) и медиана (Me) определяются по следующим формулам:
Предварительно выявим интервалы, в которых находится мода и медиана. Наибольшая частота (22) указывает на модальный интервал 30-35 млн. руб. По накопленным частотам определяем, что медиана должна находиться в том же интервале. В нашем случае их значения равны:
Для определения квартилей используются формулы, аналогичные формуле для расчета медианы. Общая схема их расчета такова: определяется номер для первой и третьей квартилей:
По накопленным частотам определяем интервалы, в которых находятся 1 и 3 квартили, соответственно: (20-25) и (30-35). Величина квартилей определяется по формулам:
Квартильное отклонение:
где
Среднее линейное отклонение:
Дисперсия:
Среднее квадратическое отклонение:
Рассчитаем относительные показатели вариации. Коэффициент осцилляции:
Относительное линейное отклонение:
Относительный показатель квартильной вариации:
Коэффициент вариации:
Определим показатели формы распределения:
Сформулируем выводы по рассчитанным показателям вариации примера 2, в котором представлен интервальный ряд распределения предприятий по объему товарооборота. Размах вариации свидетельствует о том, что разница между максимальным и минимальным значением составляет 40 млн. руб. Средний объем товарооборота – 30 млн. руб. Чаще всего встречающееся значение объема товарооборота в рассматриваемой совокупности предприятий – 31,4 млн. руб., причем 50% (40 предприятий) имеют объем товарооборота менее 30,5 млн. руб., а 50% – свыше. Соотношение Помимо Mo и Me, количественную характеристику структуры строения вариационных рядов оценивают такие порядковые статистики, как: квартили, квинтили, децили, перцинтили и др. Степень вариации ряда может быть определена также по формуле квартильного отклонения Квартильное отклонение, равное 5,0 млн. руб., свидетельствует об умеренной асимметрии распределения, так как в симметричных или умеренно асимметричных распределениях Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем колеблется величина признака у единиц исследуемой совокупности. Так, средняя величина колеблемости объема товарооборота предприятий отраслей промышленности составляет: по среднему линейному отклонению - 6,5 млн. руб. (абсолютное отклонение); по среднему квадратическому отклонению - 8,1 млн. руб. Квадрат отклонений индивидуальных значений признака от их средней величины равен 65. Разница между крайними значениями признака на 33,3% превышает его среднее значение ( Относительное линейное отклонение ( Моментный коэффициент асимметрии В связи с тем, что коэффициент осцилляции больше 1 Структурные показатели (коэффициенты) асимметрии характеризуют асимметричность только в центральной части распределения, то есть основной массы единиц, и в отличии от моментного коэффициента не зависят от крайних значений признака. Воспользовавшись структурным коэффициентом асимметрии К. Пирсона, приходим к выводу, что Соотношение
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ Таблица 6 ПРАКТИЧЕСКАЯ РАБОТА 4 Пример 1. Рассмотрим ряд распределения по первичным данным о размере прибыли 30 банков региона за год, млн. руб.
5,2 6,4 8,7 5,1 3,7 4,3 9,2 6,6 4,6 8,1 5,7 6,1 6,8 6,9 5,0
8,3 8,4 7,2 7,9 6,5 7,9 6,0 9,1 7,3 7,0 7,9 4,9 7,6 8,0 5,9.
Определяем, что 3 банка (10 % от общего числа) с наименьшим размером прибыли 3,7 млн.; 4,3 млн. и 4,6 млн. руб. имеют Для трех банков с наибольшими значениями 8,4 млн., 9,1 млн. руб. и 9,2 млн. руб. средняя арифметическая Следовательно, коэффициент фондовой дифференциации будет равен:
Это означает, что размер прибыли у 10% банков с наивысшими доходами более чем в 2 раза превышает размер прибыли 10% банков с наименьшими доходами.
Пример 2. Расчет коэффициента децильной дифференциации проведем на основе данных о распределении населения России по размеру среднедушевого денежного дохода в 2005 г. Таблица 8 ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Проанализировать по первичным данным размер прибыли 20 коммерческих палаток рынка за день, тыс. руб.
1 вариант
2,7 5,9 2,8 3,3 8,0 7,7 4,6 5,6 4,3 4,2 3,1 7,1 6,0 2,2 4,0 3,4 6,8 8,8 5,1 3,9
2 вариант 4,0 6,7 9,2 10,9 6,5 10,2 7,4 9,5 11,1 5,9 4,8 4,2 10,0 4,8 11,2 7,1 4,1 60, 5,5 7,7
3 вариант 9,4 7,2 5,1 4,3 6,6 8,8 7,6 10,9 5,7 9,3 8,5 10,8 5,9 7,4 5,3 4,0 6,3 8,1 7,8 6,0 4 вариант 4,0 12,7 5,0 3,4 6,1 5,6 2,7 4,3 3,9 6,3 4,4 2,5 2,9 5,2 3,5 4,2 12,8 6,7 5,9 2,8
5 вариант 3,7 5,2 6,0 3,8 6,6 5,9 6,8 6,5 4,4 3,4 4,0 6,9 5,6 4,1 3,9 5,3 6,2 3,3 6,4 4,5
6 вариант 2,7 4,0 3,3 4,7 5,2 2,9 4,3 8,7 5,4 3,0 3,1 5,3 8,8 2,8 4,1 3,4 6,8 2,5 4,9 6,5
Рассчитать коэффициент фондовой дифференциации, сделать выводы.
Таблица 9 ЛАБОРАТОРНАЯ РАБОТА 3
Шаг 2. Настройка таблицы. Произведем настройку размеров таблицы. Создадим столько переменных и наблюдений, сколько необходимо. Нажмите кнопку “Var” Variables (Переменные) на панели инструментов и выберите команду Delete Variables (Удаление переменных). У кажите диапазон удаляемых переменных (рис. 7). Нажмите кнопку ОК.
Рис. 7. Окно удаления ненужных переменных.
Необходимое число наблюдений – 7; в созданной таблице число наблюдений равно 10. Три лишних наблюдения из таблицы следует удалить. Для этого воспользуйтесь кнопкой “Cases” Cases (Наблюдения) и командой Delete (Удалить). В появившемся окне сделайте установки, (рис 8).
Рис. 8. Окно удаления ненужных наблюдений
Задайте диапазон удаляемых наблюдений в диалоговом окне Delete Cases (Удаление наблюдения). Нажмите кнопку ОК. Теперь электронная таблица выглядит следующим образом:
Рис. 9. Пустая таблица с одной переменной и семью наблюдениями
Если вам требуется добавить число переменных, необходимо нажать кнопку Vars и выбрать команду Add, далее указать диапазон добавляемых переменных. Аналогично можно добавить число наблюдений (Cases).
Шаг 3. Подготовка таблицы к вводу данных, заголовок таблицы и имена переменных. Дважды щелкните мышью на белом поле в таблице под словами: Data: STUD.STA 1V*7C. На экране появится окно Data File Header (Заголовок файла данных), в котором можно задать заголовок таблицы и дополнить информацию о данных. Введем заголовок таблицы: “Данные об объеме продаж валюты”, и дополнительную информацию об отделениях Центробанка, как показано на рисунке 10.
Рис. 10. Окно, в котором задается заголовок таблицы и дополнительная информация
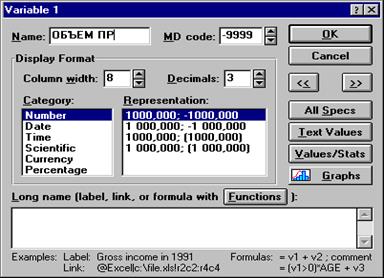
Нажмите кнопку ОК в диалоговом окне Data File Header (Заголовок файла данных). Таблица почти готова к вводу данных, однако, придадим ей еще несколько более удобный вид: введем имена переменных, которые отражают смысл записей, и специфицируем их. Дважды щелкните на имени переменной VAR1 в электронной таблице. На экране появится окно спецификации переменной VAR1. В поле Name (Имя) напишите: Объем пр. Длина имени не должна превышать 8 символов.
Рис. 11. Окно спецификации переменной VAR1.
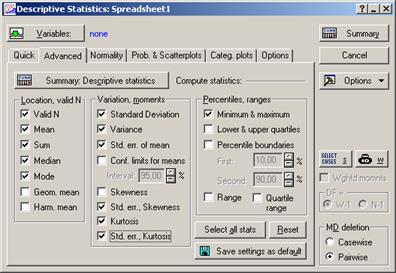
Шаг 2. В выпадающем меню высветится верхняя строчка Descriptives of Объем пр (Описательные переменной Объем пр). Выбрав необходимую переменную (Variables)и отметивгалочками необходимые характеристики ряда распределения (вкладка Advansed) (рис. 13), нажимаем кнопку Summary и электронная таблица с основными описательными статистиками для выбранной переменной появится на экране (табл. 10):
Рис. 13. Окно выбора характеристик ряда распределения
Таблица 10 Электронная таблица с описательными статистиками показателя объема продаж валюты отделениями Центробанка, Млн. руб.
Отметим, что таблица результатов отличается от таблицы с исходными данными. Этот специальный тип таблиц в STATISTICA носит название scrollsheets . Прокручивая электронную таблицу результатов, вы увидите слева направо следующие описательные статистики переменной: Объем продаж, млн. руб. Valid N – истинное число наблюдений переменной ОБЪЕМ ПРОДАЖ (число наблюдений без пропусков); Mean – выборочное Среднее; Confid – 95% – нижняя граница 95% доверительного интервала для среднего; Confid + 95% – верхняя граница 95% доверительного интервала для среднего; Sum – сумма (сумма значений переменной ОБЪЕМ ПРОДАЖ); Minimum – минимум (минимальное значение переменной ОБЪЕМ ПРОДАЖ); Maximum – максимум (максимальное значение переменной ОБЪЕМ ПРОДАЖ); Range – размах (то есть разность между максимумом и минимумом); Variance – выборочная дисперсия; Std. Dev. – стандартное отклонение; Std. Err. – стандартная ошибка; Skewness – выборочный коэффициент асимметрии; Std. Err. Skewness – стандартная ошибка коэффициента асимметрии; Kurtosis – выборочный коэффициент эксцесса; Std. Err. Kurtosis – стандартная ошибка эксцесса. ЛАБОРАТОРНАЯ РАБОТА 4 Определить дисперсию.
СТАНДОТКЛОНА - оценивает стандартное отклонение по выборке. Стандартное отклонение - это мера того, насколько широко разбросаны точки данных относительно их среднего. В расчете также учитываются текстовые и логические значения, такие как ИСТИНА или ЛОЖЬ.
СТАНДОТКЛОНА(значение1,значение2,...) Значение1, значение2,... - это от 1 до 30 значений, соответствующих выборке из генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.
· СТАНДОТКЛОНА предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНПА. · Аргументы, содержащие значение ИСТИНА, интерпретируются как 1. Аргументы, содержащие значение ЛОЖЬ, интерпретируются как 0 (ноль). Если текст и логические значения должны игнорироваться, следует использовать функцию рабочего листа СТАНДОТКЛОН. · Стандартное отклонение вычисляется с использованием "не Байесовского" или "n - 1" метода. · СТАНДОТКЛОНА использует следующую формулу: СТАНДОТКЛОНА =
СТАНДОТКЛОНП - Вычисляет стандартное отклонение по генеральной совокупности. Стандартное отклонение - это мера того, насколько широко разбросаны точки данных относительно их среднего.
СТАНДОТКЛОНП(число1; число2;...) Число1, число2,... - это от 1 до 30 числовых аргументов, соответствующих генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.
· Логические значения, такие как ИСТИНА или ЛОЖЬ, а также текст игнорируются. Если текст и логические значения игнорироваться не должны, следует использовать функцию рабочего листа СТАНДОТКЛОНА. · СТАНДОТКЛОНП предполагает, что аргументы образуют всю генеральную совокупность. Если данные являются только выборкой из генеральной совокупности, то стандартное отклонение следует вычислять с использованием функции СТАНДОТКЛОН. · Для больших выборок СТАНДОТКЛОН и СТАНДОТКЛОНП возвращают примерно равные значения. · Стандартное отклонение вычисляется с использованием "смещенного" или "n" метода. · СТАНДОТКЛОНП использует следующую формулу:
СТАНДОТКЛОНП =
СТАНДОТКЛОНПА - вычисляет стандартное отклонение по генеральной совокупности, заданной аргументами, которые могут включать текст и логические значения. Стандартное отклонение - это мера того, насколько широко разбросаны точки данных относительно их среднего.
СТАНДОТКЛОНПА(значение1,значение2,...) Значение1,значение2,... это от 1 до 30 значений, соответствующих генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.
· СТАНДОТКЛОНПА предполагает, что аргументы образуют всю генеральную совокупность. Если данные являются только выборкой из генеральной совокупности, то стандартное отклонение следует вычислять с использованием функции СТАНДОТКЛОНА. · Аргументы, содержащие значение ИСТИНА, интерпретируются как 1, аргументы, содержащие значение ЛОЖЬ, интерпретируются как 0 (ноль). Если текст и логические значения должны игнорироваться, следует использовать функцию рабочего листа СТАНДОТКЛОНП. · Для больших выборок СТАНДОТКЛОНА и СТАНДОТКЛОНПА возвращают примерно равные значения. · Стандартное отклонение вычисляется с использование "Байесовского" или "n" метода. · СТАНДОТКЛОНПА использует следующую формулу: СТАНДОТКЛОНПА = В зависимости от специфики исходной информации выберите соответствующую функцию для расчета среднего квадратического отклонения и осуществите его в порядке, аналогичном пункту 2.
5. Определить эксцесс и коэффициент асимметрии.
В MS Excel расчет эксцесса и коэффициента асимметрии реализован с помощью функций ЭКСЦЕСС И СКОС.
СКОС - Возвращает асимметрию распределения. Асимметрия характеризует степень несимметричности распределения относительно его среднего. Положительная асимметрия указывает на отклонение распределения в сторону положительных значений. Отрицательная асимметрия указывает на отклонение распределения в сторону отрицательных значений.
СКОС(число1;число2;...) Число1, число2,... - это от 1 до 30 аргументов, для которых вычисляется асимметричность. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.
· Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа. · Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения учитываются. · Если имеется менее трех точек данных, или стандартное отклонение равно нулю, то функция СКОС возвращает значение ошибки #ДЕЛ/0!. · Уравнение для асимметрии определяется следующим образом: СКОС = где ЭКСЦЕСС - Возвращает эксцесс множества данных. Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.
ЭКСЦЕСС(число1;число2;...) Число1, число2,... - это от 1 до 30 аргументов, для которых вычисляется эксцесс. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.
· Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа. · Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения учитываются. · Если задано менее четырех точек данных или если стандартное отклонение выборки равняется нулю, то функция ЭКСЦЕСС возвращает значение ошибки #ДЕЛ/0!. · Эксцесс определяется следующим образом: ЭКСЦЕСС = где Ж) нажмите ОК.
Сформулируйте выводы. 8. Расчет показателей вариации можно осуществить также с помощью «Пакета анализа». · Создать файл с исходными данными. · Запустить «Пакет анализа» В меню Сервис выберете команда Анализ данных. ( Если такая команда отсутствует в меню Сервис выбираем команду Надстройки. Устанавливаем флажок «Пакет анализа»)
Рис. 19. Запуск «Пакета анализа»
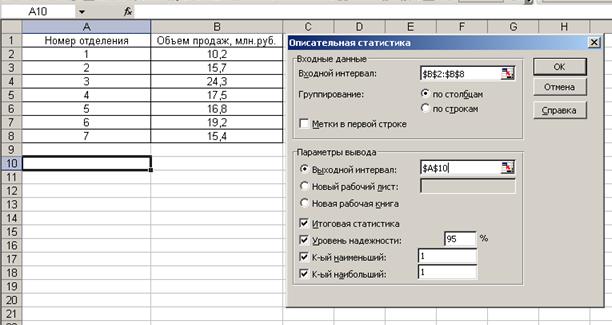
· В списке инструментов статистического анализа выбираем Описательная статистика, Это средство анализа служит для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных
Рис. 20. Выбор инструмента «Описательная статистика»
· В диалоговом окне указываем входной интервал (интервал, где расположены исходные данные). Выходной интервал (интервал, где будут указаны результаты расчетов). Некоторые сведения в этом разделе могут быть неприменимы к отдельным языкам. Входной диапазон Ссылка на диапазон, содержащий анализируемые данные. Ссылка должна состоять не менее чем из двух смежных диапазонов данных, данные в которых расположены по строкам или столбцам. Группирование Установите переключатель в положение По столбцам или По строкам в зависимости от расположения данных во входном диапазоне. Уровень надежности Установите флажок, если в выходную таблицу необходимо включить строку для уровня надежности. В поле введите требуемое значение. Например, значение 95% вычисляет уровень надежности среднего со значимостью 0.05. К-ый наибольший Установите флажок, если в выходную таблицу необходимо включить строку для k-го наибольшего значения для каждого диапазона данных. В соответствующем окне введите число k. Если k равно 1, эта строка будет содержать максимум из набора данных. К-ый наименьший Установите флажок, если в выходную таблицу необходимо включить строку для k-го наименьшего значения для каждого диапазона данных. В соответствующем окне введите число k. Если k равно 1, эта строка будет содержать минимум из набора данных. Выходной диапазон Введите ссылку на левую верхнюю ячейку выходного диапазона. Этот инструмент анализа выводит два столбца сведений для каждого набора данных. Левый столбец содержит метки статистических данных; правый столбец содержит статистические данные. Состоящий их двух столбцов диапазон статистических данных будет выведен для каждого столбца или для каждой строки входного диапазона в зависимости от положения переключателя Группирование. Новый лист Установите переключатель, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. Если в этом есть необходимость, введите имя нового листа в поле, расположенном напротив соответствующего положения переключателя. Новая книга Установите переключатель, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге. Итоговая статистика Установите флажок, если в выходном диапазоне необходимо получить по одному полю для каждого из следующих видов статистических данных: Среднее, Стандартная ошибка (среднего), Медиана, Мода, Стандартное отклонение, Дисперсия выборки, Эксцесс, Асимметричность, Интервал, Минимум, Максимум, Сумма, Счет, Наибольшее (#), Наименьшее (#), Уровень надежности.
Рис. 21. Работа в диалоговом окне «Описательная статистика»
· В результате получим следующие показатели
Таблица 12 СПИСОК ЛИТЕРАТУРЫ
1. Глинский, В.В., Ионин, В.Г. Статистический анализ [Текст]: Учеб. пособие. – М.: Филин, 1998. – 264 с. 2. Громыко, Г.Л. Общая теория статистики: Практикум. [Текст]. – М.: ИНФРА-М, 1999. – 139 с. 3. Громыко, Г.Л. Теория статистики: практикум [Текст]. – М.: ИНФРА-М, 2001. – 160 с. 4. Гусаров, В.М. Теория статистики [Текст]: Учеб. пособие для ВУЗов. – М: Аудит, ЮНИТИ, 1998. – 247 с. 5. Ефимова, М.Р., Рябцев, В.М. Общая теория статистики. [Текст]. – М: Финансы и статистика, 1991. – 302 с. 6. Мармоза, А.Т. Практикум по математической статистике [Текст]: Учебное пособие. – К.: Выща школа, 1990. – 191 с. 7. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности [Текст]: Учебник / А.И. Харламов, О.Э. Башина, В.Т. Пабурин. Под ред. Спирина А.А., О.Э. Башиной / М.: Финансы и статистика, 1994. – 296 с. 8. Практикум по общей теории статистики [Текст]: Учеб. пособие / Н.Н. Ряузов и др. – 2-е изд. – М.: Финансы и статистика, 1981. – 278 с. 9. Салин, В.Н., Чурилова, Э.Ю. Курс теории статистики для подготовки специалистов финансово-экономического профиля [Текст]: Учебник. – М.: Финансы и статистика, 2006. – 480 с. 10. Сборник задач по общей теории статистики [Текст]: Учебное пособие/ И.С. Пасхавер, А.Л. Яблочник, Н.Т.Иващенко и др. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 1983. – 280 с. 11. Практикум по теории статистики [Текст]: /Под. ред. Р.А. Шмойловой – М.: Финансы и статистика, 1999. – 414 с. 12. Статистика [Текст]: Курс лекций / Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др. Под ред. к.э.н. В.Г. Ионина. – Новосибирск: изд-во НГА и У, 1996. – 310 с. 13. Статистик а [Текст]: Методические указания к выполнению практ. и лаб. работ. Часть 2 /Л.И. Бернасовская, Н.И. Гришакина, Г.В. Лебедева, О.Д. Притула, Г.В. Фетисова.- НовГУ им. Я.Мудрого, 2005.-56с. 14. Статистика рынка товаров и услуг [Текст]: Учебник / И.К. Белявский, П.Д. Кулагина, А.В. Коротков и др. Под ред. И.К. Белявской – М.: Финансы и статистика, 1995. – 432 с. 15. Статистика [Текст]: Учебное пособие./ А.В. Багат, М.М. Конкина, В.М. Сим
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 503; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.015 с.) |

 ,
, – наибольшее значение варьирующего признака;
– наибольшее значение варьирующего признака;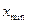 – наименьшее значение варьирующего признака.
– наименьшее значение варьирующего признака. ,
, и
и  – соответственно первая и третья квартили распределения.
– соответственно первая и третья квартили распределения. ; 25% единиц будут заключены между
; 25% единиц будут заключены между  и
и  ,
, где
где  – нижняя граница интервала, в котором находится первая квартиль;
– нижняя граница интервала, в котором находится первая квартиль; – сумма накопленных частот интервалов, предшествующих интервалу, в котором находится первая квартиль;
– сумма накопленных частот интервалов, предшествующих интервалу, в котором находится первая квартиль; – частота интервала, в котором находится первая квартиль.
– частота интервала, в котором находится первая квартиль. ,
, ,
, ) представляет собой среднюю величину из абсолютных отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения.
) представляет собой среднюю величину из абсолютных отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения.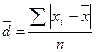 - невзвешенное среднее линейное отклонение,
- невзвешенное среднее линейное отклонение, - взвешенное среднее линейное отклонение.
- взвешенное среднее линейное отклонение. ) – средний квадрат отклонений индивидуальных значений признака от их средней величины. Дисперсия вычисляется по формулам простой невзвешенной и взвешенной.
) – средний квадрат отклонений индивидуальных значений признака от их средней величины. Дисперсия вычисляется по формулам простой невзвешенной и взвешенной. - невзвешенная,
- невзвешенная,  - взвешенная.
- взвешенная.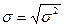
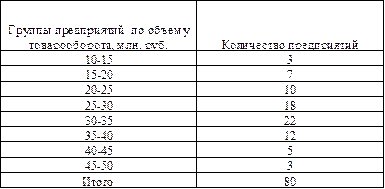

 млн. руб.
млн. руб. млн. руб.
млн. руб.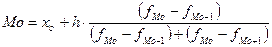

 млн. руб.
млн. руб. млн. руб.
млн. руб.
 .
.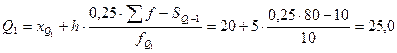 млн. руб.
млн. руб. млн. руб.
млн. руб. млн. руб.
млн. руб. млн. руб.
млн. руб. – соответственно первая и третья квартили распределения.
– соответственно первая и третья квартили распределения.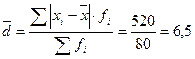 млн. руб.
млн. руб.
 млн. руб.
млн. руб.




 характерно для левосторонней асимметрии, при котором большая часть единиц совокупности имеет значение признака ниже модального. Нашему примеру соответствует соотношение 30 млн. руб. < 30,5 млн. руб.< 31,4 млн. руб., что свидетельствует о том, что большая часть анализируемых предприятий имела объем товарооборота ниже, чем его модальное значение (31,4 млн. руб.).
характерно для левосторонней асимметрии, при котором большая часть единиц совокупности имеет значение признака ниже модального. Нашему примеру соответствует соотношение 30 млн. руб. < 30,5 млн. руб.< 31,4 млн. руб., что свидетельствует о том, что большая часть анализируемых предприятий имела объем товарооборота ниже, чем его модальное значение (31,4 млн. руб.). , предложенной английским биологом и антропологом Ф. Гальтоном. Это абсолютный квартильный показатель вариации.
, предложенной английским биологом и антропологом Ф. Гальтоном. Это абсолютный квартильный показатель вариации. (в рассматриваемом примере
(в рассматриваемом примере  ).
). = 133,3%).
= 133,3%). = 21,7%) и относительный показатель квартильной вариации (
= 21,7%) и относительный показатель квартильной вариации (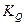 = 16,4%) характеризуют однородность исследуемой совокупности, что подтверждает рассчитанный коэффициент вариации, равный 27% (
= 16,4%) характеризуют однородность исследуемой совокупности, что подтверждает рассчитанный коэффициент вариации, равный 27% ( =27% меньше 30%).
=27% меньше 30%). в очередной раз подтверждает наличие незначительной левосторонней асимметрии. Основной недостаток моментного коэффициента асимметрии заключается в том, что его величина зависит от наличия в совокупности резко выделяющихся единиц и следовательно его большая (абсолютная) величина будет объясняться доминирующим вкладом в величину центрального момента третьего порядка нетипичных значений, а не асимметричностью распределения основной части единиц.
в очередной раз подтверждает наличие незначительной левосторонней асимметрии. Основной недостаток моментного коэффициента асимметрии заключается в том, что его величина зависит от наличия в совокупности резко выделяющихся единиц и следовательно его большая (абсолютная) величина будет объясняться доминирующим вкладом в величину центрального момента третьего порядка нетипичных значений, а не асимметричностью распределения основной части единиц. , то есть размах вариации на 33 % превышает среднее значение объема товарооборота целесообразно либо исключить из анализа резко отличающиеся единицы совокупности, либо воспользоваться структурными показателями асимметрии.
, то есть размах вариации на 33 % превышает среднее значение объема товарооборота целесообразно либо исключить из анализа резко отличающиеся единицы совокупности, либо воспользоваться структурными показателями асимметрии.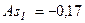 свидетельствует в пользу полученных ранее результатов.
свидетельствует в пользу полученных ранее результатов. и
и  с соответствующей средней квадратической ошибкой позволяет утверждать о том, что асимметрия и эксцесс являются несущественными.
с соответствующей средней квадратической ошибкой позволяет утверждать о том, что асимметрия и эксцесс являются несущественными. = 4,2 млн. руб.
= 4,2 млн. руб. составляет 8,9 млн. руб.
составляет 8,9 млн. руб.



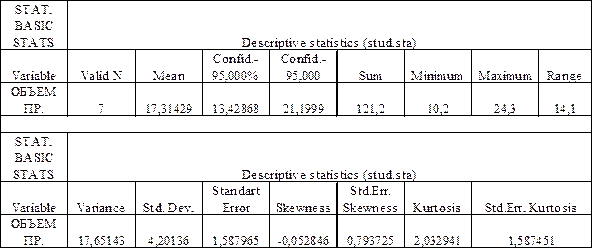


 ,
, - стандартное отклонение выборки.
- стандартное отклонение выборки.