
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Данные об объеме продаж валюты нескольких отделений Центробанка.Содержание книги
Поиск на нашем сайте
Определить средний объем продаж валюты по совокупности отделений, рассчитать абсолютные и относительные показатели вариации. Рассчитаем размах вариации: R = Для определения отклонений значений признака от средней и их квадратов строим вспомогательную таблицу:
Таблица 2 Расчетная таблица
Среднее значение находим по формуле средней арифметической простой:
Среднее линейное отклонение:
Дисперсия:
Среднее квадратическое отклонение:
Рассчитаем относительные показатели вариации. Коэффициент осцилляции:
Относительное линейное отклонение:
Коэффициент вариации:
Для расчета показателей формы распределения строим вспомогательную таблицу:
Таблица 3 Расчетная таблица
Далее рассчитываем показатели асимметрии, эксцесса и их ошибки:
Абсолютные показатели вариации: размах вариации Соотношение
Для нормального распределения это соотношение равно 1,25, следовательно, данная совокупность близка к нормальному распределению. Относительные показатели вариации: относительный размах вариации (коэффициент осцилляции), относительное линейное отклонение, коэффициент вариации - служат критериями оценки интенсивности вариации. Наиболее распространенным из них является коэффициент вариации. В нашем случае его величина составила 23,2 %, что так же свидетельствует о небольшом разбросе значений признака вокруг средней, и, следовательно, об однородности совокупности. К аналогичному выводу подталкивает и значение коэффициента осцилляции (82,9%), указывающего на то, что размах вариации несущественен, а именно на 17,1 % меньше среднего значения объема продаж валюты. Асимметрия и эксцесс являются важнейшими характеристиками формы распределения. Для оценки степени асимметричности в анализе использован моментный коэффициент (стандартизованный момент третьего порядка). Оценка степени существенности асимметрии проведена с использованием средней квадратической ошибки коэффициента асимметрии, которая зависит от объема изучаемой совокупности. Так как отношение Проведенное исследование позволяет утверждать, что анализируемый ряд распределения близок к симметричному и, следовательно, существует возможность рассмотреть еще одно свойство рядов распределения – эксцесс. Отрицательный эксцесс Средняя квадратическая ошибка эксцесса Пример 2.
Таблица 4 Данные о товарообороте предприятий одной из отраслей промышленности.
Определить средний объем товарооборота, структурные средние, абсолютные и относительные показатели вариации и насколько фактическое распределение согласуется с нормальным (по показателям формы распределения). Для расчета показателей построим вспомогательную таблицу.
Таблица 5 Расчетная таблица
Размах вариации:
Среднее значение находим по формуле средней арифметической взвешенной:
В равноинтервальных рядах распределения мода (Mo) и медиана (Me) определяются по следующим формулам:
Предварительно выявим интервалы, в которых находится мода и медиана. Наибольшая частота (22) указывает на модальный интервал 30-35 млн. руб. По накопленным частотам определяем, что медиана должна находиться в том же интервале. В нашем случае их значения равны:
Для определения квартилей используются формулы, аналогичные формуле для расчета медианы. Общая схема их расчета такова: определяется номер для первой и третьей квартилей:
По накопленным частотам определяем интервалы, в которых находятся 1 и 3 квартили, соответственно: (20-25) и (30-35). Величина квартилей определяется по формулам:
Квартильное отклонение:
где
Среднее линейное отклонение:
Дисперсия:
Среднее квадратическое отклонение:
Рассчитаем относительные показатели вариации. Коэффициент осцилляции:
Относительное линейное отклонение:
Относительный показатель квартильной вариации:
Коэффициент вариации:
Определим показатели формы распределения:
Сформулируем выводы по рассчитанным показателям вариации примера 2, в котором представлен интервальный ряд распределения предприятий по объему товарооборота. Размах вариации свидетельствует о том, что разница между максимальным и минимальным значением составляет 40 млн. руб. Средний объем товарооборота – 30 млн. руб. Чаще всего встречающееся значение объема товарооборота в рассматриваемой совокупности предприятий – 31,4 млн. руб., причем 50% (40 предприятий) имеют объем товарооборота менее 30,5 млн. руб., а 50% – свыше. Соотношение Помимо Mo и Me, количественную характеристику структуры строения вариационных рядов оценивают такие порядковые статистики, как: квартили, квинтили, децили, перцинтили и др. Степень вариации ряда может быть определена также по формуле квартильного отклонения Квартильное отклонение, равное 5,0 млн. руб., свидетельствует об умеренной асимметрии распределения, так как в симметричных или умеренно асимметричных распределениях Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем колеблется величина признака у единиц исследуемой совокупности. Так, средняя величина колеблемости объема товарооборота предприятий отраслей промышленности составляет: по среднему линейному отклонению - 6,5 млн. руб. (абсолютное отклонение); по среднему квадратическому отклонению - 8,1 млн. руб. Квадрат отклонений индивидуальных значений признака от их средней величины равен 65. Разница между крайними значениями признака на 33,3% превышает его среднее значение ( Относительное линейное отклонение ( Моментный коэффициент асимметрии В связи с тем, что коэффициент осцилляции больше 1 Структурные показатели (коэффициенты) асимметрии характеризуют асимметричность только в центральной части распределения, то есть основной массы единиц, и в отличии от моментного коэффициента не зависят от крайних значений признака. Воспользовавшись структурным коэффициентом асимметрии К. Пирсона, приходим к выводу, что Соотношение
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ Таблица 6
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

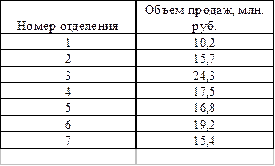
 = 24,3 - 10,2 = 14,1 млн. руб.
= 24,3 - 10,2 = 14,1 млн. руб.
 млн. руб.
млн. руб.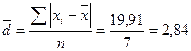 млн. руб.
млн. руб.
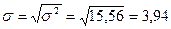 млн. руб.
млн. руб.





 , среднее линейное отклонение
, среднее линейное отклонение  , среднее квадратическое отклонение
, среднее квадратическое отклонение 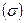 и дисперсия
и дисперсия  , характеризуют размер вариации. Размах вариации (14,10 млн. руб.) зависит только от крайних значений в совокупности. Более точно характеризуют вариацию признака показатели, основанные на учете колеблемости всех его значений – среднее линейное отклонение
, характеризуют размер вариации. Размах вариации (14,10 млн. руб.) зависит только от крайних значений в совокупности. Более точно характеризуют вариацию признака показатели, основанные на учете колеблемости всех его значений – среднее линейное отклонение  млн. руб., по формуле среднеквадратического отклонения
млн. руб., по формуле среднеквадратического отклонения  млн. руб.
млн. руб. может служить индикатором «засоренности» нетипичными, выделяющимися из основной массы единицами.
может служить индикатором «засоренности» нетипичными, выделяющимися из основной массы единицами. .
.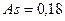 . На направление асимметрии указывает знак коэффициента:
. На направление асимметрии указывает знак коэффициента: 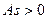 , следовательно, в данном случае правосторонняя (положительная) асимметрия. Так как относительные показатели вариации незначительны (
, следовательно, в данном случае правосторонняя (положительная) асимметрия. Так как относительные показатели вариации незначительны ( и
и  ), и в частности, коэффициент осцилляции меньше 1, правомерно утверждение, что в совокупности нет резко выделяющихся единиц, и нетипичные значения не будут доминировать в величине центрального момента третьего порядка, таким образом можно ограничиться расчетом моментного коэффициента асимметрии.
), и в частности, коэффициент осцилляции меньше 1, правомерно утверждение, что в совокупности нет резко выделяющихся единиц, и нетипичные значения не будут доминировать в величине центрального момента третьего порядка, таким образом можно ограничиться расчетом моментного коэффициента асимметрии. , то асимметрия признается несущественной, вызванной влиянием случайных обстоятельств.
, то асимметрия признается несущественной, вызванной влиянием случайных обстоятельств. характеризует более плосковершинное, чем нормальное распределение, а также указывает на то, что в совокупности нет слабоварьирующего по данному признаку «ядра» и единицы рассеяны по всем значениям признака более равномерно.
характеризует более плосковершинное, чем нормальное распределение, а также указывает на то, что в совокупности нет слабоварьирующего по данному признаку «ядра» и единицы рассеяны по всем значениям признака более равномерно. позволяет оценить его существенность. Полученный результат
позволяет оценить его существенность. Полученный результат 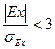 , и, следовательно, отклонение от нормального можно считать несущественным.
, и, следовательно, отклонение от нормального можно считать несущественным.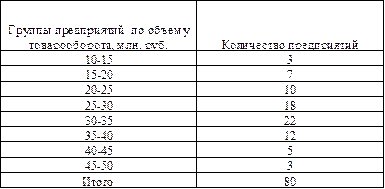

 млн. руб.
млн. руб. млн. руб.
млн. руб.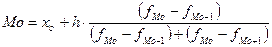

 млн. руб.
млн. руб. млн. руб.
млн. руб.
 .
.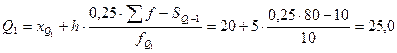 млн. руб.
млн. руб. млн. руб.
млн. руб. млн. руб.
млн. руб. млн. руб.
млн. руб. и
и  – соответственно первая и третья квартили распределения.
– соответственно первая и третья квартили распределения.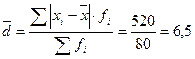 млн. руб.
млн. руб.
 млн. руб.
млн. руб.




 характерно для левосторонней асимметрии, при котором большая часть единиц совокупности имеет значение признака ниже модального. Нашему примеру соответствует соотношение 30 млн. руб. < 30,5 млн. руб.< 31,4 млн. руб., что свидетельствует о том, что большая часть анализируемых предприятий имела объем товарооборота ниже, чем его модальное значение (31,4 млн. руб.).
характерно для левосторонней асимметрии, при котором большая часть единиц совокупности имеет значение признака ниже модального. Нашему примеру соответствует соотношение 30 млн. руб. < 30,5 млн. руб.< 31,4 млн. руб., что свидетельствует о том, что большая часть анализируемых предприятий имела объем товарооборота ниже, чем его модальное значение (31,4 млн. руб.). , предложенной английским биологом и антропологом Ф. Гальтоном. Это абсолютный квартильный показатель вариации.
, предложенной английским биологом и антропологом Ф. Гальтоном. Это абсолютный квартильный показатель вариации. (в рассматриваемом примере
(в рассматриваемом примере  ).
). = 133,3%).
= 133,3%). = 21,7%) и относительный показатель квартильной вариации (
= 21,7%) и относительный показатель квартильной вариации (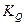 = 16,4%) характеризуют однородность исследуемой совокупности, что подтверждает рассчитанный коэффициент вариации, равный 27% (
= 16,4%) характеризуют однородность исследуемой совокупности, что подтверждает рассчитанный коэффициент вариации, равный 27% ( =27% меньше 30%).
=27% меньше 30%). в очередной раз подтверждает наличие незначительной левосторонней асимметрии. Основной недостаток моментного коэффициента асимметрии заключается в том, что его величина зависит от наличия в совокупности резко выделяющихся единиц и следовательно его большая (абсолютная) величина будет объясняться доминирующим вкладом в величину центрального момента третьего порядка нетипичных значений, а не асимметричностью распределения основной части единиц.
в очередной раз подтверждает наличие незначительной левосторонней асимметрии. Основной недостаток моментного коэффициента асимметрии заключается в том, что его величина зависит от наличия в совокупности резко выделяющихся единиц и следовательно его большая (абсолютная) величина будет объясняться доминирующим вкладом в величину центрального момента третьего порядка нетипичных значений, а не асимметричностью распределения основной части единиц. , то есть размах вариации на 33 % превышает среднее значение объема товарооборота целесообразно либо исключить из анализа резко отличающиеся единицы совокупности, либо воспользоваться структурными показателями асимметрии.
, то есть размах вариации на 33 % превышает среднее значение объема товарооборота целесообразно либо исключить из анализа резко отличающиеся единицы совокупности, либо воспользоваться структурными показателями асимметрии.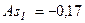 свидетельствует в пользу полученных ранее результатов.
свидетельствует в пользу полученных ранее результатов. и
и  с соответствующей средней квадратической ошибкой позволяет утверждать о том, что асимметрия и эксцесс являются несущественными.
с соответствующей средней квадратической ошибкой позволяет утверждать о том, что асимметрия и эксцесс являются несущественными.


