
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Размах вариации, квартильное отклонение, среднее линейное и квадратическое отклонения – величины именованные, имеют размерность осредняемого признака. Дисперсия единицы измерения не имеет.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях вычисляются относительные показатели вариации. Базой для сравнения служит средняя арифметическая. Чаще всего относительные показатели выражаются в процентах и характеризуют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Коэффициент осцилляции (относительный размах вариации) рассчитывается по формуле:
Линейный коэффициент вариации (относительное линейное отклонение):
Относительный показатель квартильной вариации:
Коэффициент вариации:
Наиболее часто применяемый в статистике показатель относительной колеблемости – коэффициент вариации. Его используют не только для сравнительной оценки вариации, но и как характеристику однородности совокупности. Чем больше величина коэффициента вариации, тем больше разброс значений признака вокруг средней, тем больше неоднородность совокупности. Существует шкала определения степени однородности совокупности в зависимости от значений коэффициента вариации (17; С.61).
Для получения приблизительного представления о форме распределения строят графики распределения (полигон и гистограмму). В практике статистического исследования приходится встречаться с самыми различными распределениями. При изучении однородных совокупностей имеем дело, как правило, с одновершинными распределениями. Многовершинность свидетельствует о неоднородности изучаемой совокупности, появление двух и более вершин говорит о необходимости перегруппировки данных с целью выделения более однородных групп. Выяснение общего характера распределения предполагает оценку степени его однородности, а также вычисление показателей асимметрии и эксцесса. Симметричным является распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричных распределений средняя арифметическая, мода и медиана равны между собой. В связи с этим простейший показатель асимметрии основан на соотношении показателей центра распределения: чем больше разница между средними
Для характеристики асимметричности в центральной части распределения, то есть основной массы единиц или для сравнительного анализа степени асимметрии нескольких распределений рассчитывают относительный показатель асимметрии К.Пирсона:
Величина показателя As может быть положительной и отрицательной. Положительная величина показателя указывает на наличие правосторонней асимметрии (правая ветвь относительно максимальной ординаты вытянута больше, чем левая). При правосторонней асимметрии между показателями центра распределения существует соотношение:
Рис. 1. Распределение: 1 – с левосторонней асимметрией; 2 – с правосторонней асимметрией.
Другой показатель, предложенный шведским математиком Линдбергом, рассчитывают по формуле:
где П – процент тех значений признака, которые превосходят по величине среднюю арифметическую. Наиболее точным и распространенным является показатель, основанный на определении центрального момента третьего порядка (в симметричном распределении его величина равна нулю):
где
σ – среднеквадратическое отклонение. Применение этого показателя дает возможность не только определить величину асимметрии, но и ответить на вопрос о наличии или отсутствии асимметрии в распределении признака в генеральной совокупности. Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, которая зависит от объема наблюдений n и рассчитывается по формуле:
Если отношение Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Линдбергом предложен следующий показатель для оценки эксцесса:
где П – доля (%) количества вариантов, лежащих в интервале, равном половине среднего квадратического отклонения в ту или другую сторону от средней арифметической. Наиболее точным является показатель, использующий центральный момент четвертого порядка:
где
На рисунке 2 представлены два распределения: одно – островершинное (величина эксцесса положительная), второе – плосковершинное (величина эксцесса отрицательная). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. В нормальном распределении отношение
Рис. 2. Распределение: 1,4 – нормальное; 2 – островершинное; 3 – плосковершинное
Средняя квадратическая ошибка эксцесса рассчитывается по формуле:
где n – число наблюдений. Если Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное эмпирическое исследование к типу кривых нормального распределения.
2. Рассмотрим методику исчисления показателей вариации.
Пример 1. Таблица 1
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 600; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.249.160 (0.01 с.) |

 ,
, ,
, или
или 
 ,
,
 , тем больше асимметрия ряда.
, тем больше асимметрия ряда. .
. . Отрицательный знак показателя асимметрии свидетельствует о наличии левосторонней асимметрии (рис. 1). Между показателями центра распределения в этом случае имеется соотношение:
. Отрицательный знак показателя асимметрии свидетельствует о наличии левосторонней асимметрии (рис. 1). Между показателями центра распределения в этом случае имеется соотношение:  .
.

 ,
, ,
, - центральный момент третьего порядка:
- центральный момент третьего порядка: - для несгруппированных данных;
- для несгруппированных данных; - для сгруппированных данных.
- для сгруппированных данных. .
. , асимметрия существенна, и распределение признака в генеральной совокупности не является симметричным. Если отношение
, асимметрия существенна, и распределение признака в генеральной совокупности не является симметричным. Если отношение 
 ,
, ,
,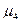 - центральный момент четвертого момента;
- центральный момент четвертого момента; - для несгруппированных данных;
- для несгруппированных данных; - для сгруппированных данных.
- для сгруппированных данных. .
.
 ,
, , то эксцесс существенен, если
, то эксцесс существенен, если  , то несущественен.
, то несущественен.


