Сроткл - возвращает среднее абсолютных значений отклонений точек данных от среднего. Сроткл является мерой разброса множества данных.

 

СРОТКЛ(число1; число2;...)

Число1, число2,... - это от 1 до 30 аргументов, для которых определяется среднее абсолютных отклонений. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

· Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.

· Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения учитываются.

· Уравнение для среднего отклонения следующее:

СРОТКЛ =

На результат СРОТКЛ влияют единицы измерения входных данных.

 

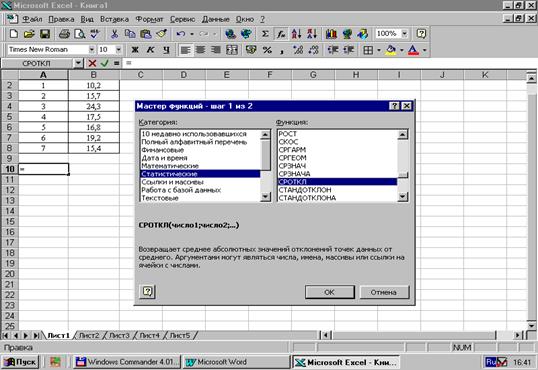
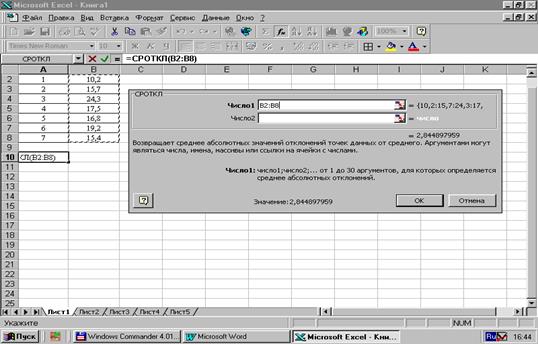
Порядок расчетов:

а) активизируйте ячейку для размещения значения СРОТКЛ;

б) войдите в “Мастер функций”;

в) выберите категорию “Статистические”;

г) выберите функцию СРОТКЛ (рис. 17);

д) нажмите ОК;

е) укажите блок значений исходных данных, по которым будет производиться расчет (рис. 16);

ж) нажмите ОК.

 

Рис. 16. Выбор функции СРОТКЛ

 

Рис. 17. Определение диапазона исходных данных

Определить среднее квадратическое отклонение.

 

В MS Excel среднее квадратическое отклонение реализовано с помощью функций СТАНДОТКЛОН, СТАНДОТКЛОНА, СТАНДОТКЛОНП, СТАНДОТКЛОНПА.

 

СТАНДОТКЛОН - оценивает стандартное отклонение по выборке. Стандартное отклонение - это мера того, насколько широко разбросаны точки данных относительно их среднего.

 

СТАНДОТКЛОН(число1; число2;...)

Число1, число2,... - это от 1 до 30 числовых аргументов, соответствующих выборке из генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

 

· Логические значения, такие как ИСТИНА или ЛОЖЬ, а также текст игнорируются. Если текст и логические значения игнорироваться не должны, следует использовать функцию рабочего листа СТАНДОТКЛОНА.

· СТАНДОТКЛОН предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНП.

· Стандартное отклонение вычисляется с использованием "несмещенного" или "n - 1" метода.

· СТАНДОТКЛОН использует следующую формулу:

СТАНДОТКЛОН =

 

СТАНДОТКЛОНА - оценивает стандартное отклонение по выборке. Стандартное отклонение - это мера того, насколько широко разбросаны точки данных относительно их среднего. В расчете также учитываются текстовые и логические значения, такие как ИСТИНА или ЛОЖЬ.

 

СТАНДОТКЛОНА(значение1,значение2,...)

Значение1, значение2,... - это от 1 до 30 значений, соответствующих выборке из генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

 

· СТАНДОТКЛОНА предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНПА.

· Аргументы, содержащие значение ИСТИНА, интерпретируются как 1. Аргументы, содержащие значение ЛОЖЬ, интерпретируются как 0 (ноль). Если текст и логические значения должны игнорироваться, следует использовать функцию рабочего листа СТАНДОТКЛОН.

· Стандартное отклонение вычисляется с использованием "не Байесовского" или "n - 1" метода.

· СТАНДОТКЛОНА использует следующую формулу:

СТАНДОТКЛОНА =

 

СТАНДОТКЛОНП - Вычисляет стандартное отклонение по генеральной совокупности. Стандартное отклонение - это мера того, насколько широко разбросаны точки данных относительно их среднего.

 

СТАНДОТКЛОНП(число1; число2;...)

Число1, число2,... - это от 1 до 30 числовых аргументов, соответствующих генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

 

· Логические значения, такие как ИСТИНА или ЛОЖЬ, а также текст игнорируются. Если текст и логические значения игнорироваться не должны, следует использовать функцию рабочего листа СТАНДОТКЛОНА.

· СТАНДОТКЛОНП предполагает, что аргументы образуют всю генеральную совокупность. Если данные являются только выборкой из генеральной совокупности, то стандартное отклонение следует вычислять с использованием функции СТАНДОТКЛОН.

· Для больших выборок СТАНДОТКЛОН и СТАНДОТКЛОНП возвращают примерно равные значения.

· Стандартное отклонение вычисляется с использованием "смещенного" или "n" метода.

· СТАНДОТКЛОНП использует следующую формулу:

 

СТАНДОТКЛОНП =

СТАНДОТКЛОНПА - вычисляет стандартное отклонение по генеральной совокупности, заданной аргументами, которые могут включать текст и логические значения. Стандартное отклонение - это мера того, насколько широко разбросаны точки данных относительно их среднего.

 

СТАНДОТКЛОНПА(значение1,значение2,...)

Значение1,значение2,... это от 1 до 30 значений, соответствующих генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

 

· СТАНДОТКЛОНПА предполагает, что аргументы образуют всю генеральную совокупность. Если данные являются только выборкой из генеральной совокупности, то стандартное отклонение следует вычислять с использованием функции СТАНДОТКЛОНА.

· Аргументы, содержащие значение ИСТИНА, интерпретируются как 1, аргументы, содержащие значение ЛОЖЬ, интерпретируются как 0 (ноль). Если текст и логические значения должны игнорироваться, следует использовать функцию рабочего листа СТАНДОТКЛОНП.

· Для больших выборок СТАНДОТКЛОНА и СТАНДОТКЛОНПА возвращают примерно равные значения.

· Стандартное отклонение вычисляется с использование "Байесовского" или "n" метода.

· СТАНДОТКЛОНПА использует следующую формулу:

СТАНДОТКЛОНПА =

В зависимости от специфики исходной информации выберите соответствующую функцию для расчета среднего квадратического отклонения и осуществите его в порядке, аналогичном пункту 2.

 

5. Определить эксцесс и коэффициент асимметрии.

 

В MS Excel расчет эксцесса и коэффициента асимметрии реализован с помощью функций ЭКСЦЕСС И СКОС.

 

СКОС - Возвращает асимметрию распределения. Асимметрия характеризует степень несимметричности распределения относительно его среднего. Положительная асимметрия указывает на отклонение распределения в сторону положительных значений. Отрицательная асимметрия указывает на отклонение распределения в сторону отрицательных значений.

 

СКОС(число1;число2;...)

Число1, число2,... - это от 1 до 30 аргументов, для которых вычисляется асимметричность. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

 

· Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.

· Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения учитываются.

· Если имеется менее трех точек данных, или стандартное отклонение равно нулю, то функция СКОС возвращает значение ошибки #ДЕЛ/0!.

· Уравнение для асимметрии определяется следующим образом:

СКОС = ,

где - стандартное отклонение выборки.

ЭКСЦЕСС - Возвращает эксцесс множества данных. Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.

 

ЭКСЦЕСС(число1;число2;...)

Число1, число2,... - это от 1 до 30 аргументов, для которых вычисляется эксцесс. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

 

· Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.

· Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения учитываются.

· Если задано менее четырех точек данных или если стандартное отклонение выборки равняется нулю, то функция ЭКСЦЕСС возвращает значение ошибки #ДЕЛ/0!.

· Эксцесс определяется следующим образом:

ЭКСЦЕСС =

где - стандартное отклонение выборки.