
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Методичний інструментарій оцінки потенціалу підприємстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основні питання теми 5.1. Загальна характеристика методичного інструментарію оцінки вартості потенціалу підприємства. 5.2. Основні методичні підходи до оцінки вартості потенціалу підприємства. 5.3. Класифікаційна характеристики інформації, яка приймає участь в оцінці потенціалу підприємства.
Загальна характеристика методичного інструментарію Оцінки вартості потенціалу підприємства
Оцінка вартості потенціалу підприємства безпосередньо пов’язана з теорією зміни вартості грошей у часі, тому що: – по-перше, існує певний часовий лаг між моментом вкладання коштів у підприємство як об’єкт оцінки та моментом отримання доходів від користування ним як товаром; – по-друге, існування такого часового лагу обумовлює необхідність урахування як інфляційних очікувань, так і ризику неотримання прогнозованих доходів. Тому для нівелювання впливу фактору часу та забезпечення порівнянності вартісних показників, які прогнозуються на різні моменти часу, в теорії зміни вартості грошей застосовується часова оцінка грошових потоків. Процедура проведення такої оцінки ґрунтується на певних припущеннях [57]: – грошовий потік – це грошові суми, що виникають в певній хронологічній послідовності; – грошовий потік, в якому всі суми розрізняються за величиною, називають звичайним грошовим потоком; – грошовий потік, в якому всі суми рівновеликі та виникають через однакові проміжки часу, називають аннуітетом; – грошовий потік може виникати наприкінці, на початку та в середині періоду; – дохід, одержуваний на інвестований капітал, з господарського обороту не вилучається, а приєднується до основного капіталу; – часова оцінка грошових потоків враховує ризики, пов'язані з інвестуванням; – ризик – це вірогідність отримання в майбутньому доходу, співпадаючого з прогнозною величиною; – ставка доходу на інвестиції – це процентне співвідношення між чистим доходом і вкладеним капіталом. Часова оцінка грошових потоків передбачає використання шести стандартних функцій складного процента, або шести функцій грошової одиниці [31, 57, 65]: 1) майбутня вартість одиниці (складний процент); 2) поточна вартість одиниці (дисконтування); 3) поточна вартість аннуітета; 4) періодичний внесок на погашення кредиту; 5) майбутня вартість аннуітета; 6) періодичний внесок до фонду накопичення. Для полегшення розрахунків в процесі оцінки грошових потоків із визначеними характеристиками (процента ставка і період нарахування процентів) в оцінній практиці застосовують так звані фінансові таблиці (додаток 1). 1. Майбутня вартість одиниці (складний процент). Розрахунки майбутньої вартості здійснюються за формулою:
де FV – майбутня вартість; PV – первинний внесок (поточна вартість); r – процентна ставка (ставка дисконту); п – число періодів нарахування процентів. Множник Дана функція дозволяє визначити майбутню вартість суми, яку має інвестор сьогодні, виходячи із ставки процента, терміну накопичення та періодичності нарахування процентів, що передбачаються. Логіка розрахунків майбутньої вартості наведена на рис. 5.1.
Рис. 5.1. Зростання основної суми за функцією майбутньої вартості
Таким чином, використання даної функції передбачає нарахування процентів не тільки на суму первинного внеску, але і на суму процентів, які накопичуються наприкінці кожного періоду. Це можливо тільки за умов реінвестування нарахованих процентів, що збільшує суму основного капіталу. Приклад. Вартість адміністративних будівель підприємства оцінюється в 150 тис. грн. Прогнозується її щорічне зростання на 12 % з урахуванням перспективності місця розташування та потенційного попиту на аналогічні об’єкти. Визначити майбутню вартість адміністративних будівель через 5 років. Майбутню вартість визначимо за формулою (5.1), значення фактору майбутньої вартості для r = 12% і n = 5 років знаходимо в додатку1:
За умов більш короткого періоду накопичення (місяць, квартал, тиждень і т.д.) процентну ставку та число періодів нарахування процентів у формулі (5.1) необхідно відкоригувати. Так, наприклад, якщо передбачається нарахування процентів щомісячно, базова формула (5.1) трансформується у такий вигляд:
Для щоквартального нарахування процентів формула майбутньої вартості має вигляд:
Приклад. Власник планує продавати свій бізнес через 1 рік за попередньою оцінною вартістю в100 тис. грн. Чи достатнім для придбання бізнесу через 1 рік буде внесок у розмірі 80 тис. грн., якщо річна банківська процента ставка становить 20 %, а нарахування процентів відбувається щоквартально? Майбутню вартість внеску визначимо за формулою (5.2).
Таким чином, внесок у розмірі 80 тис. грн. під 20 % річних із щоквартальним нарахуванням процентів буде недостатнім для придбання через рік бізнесу майбутньої вартістю 100 тис. грн. (97,24 < 100). 2. Поточна вартість одиниці (дисконтування). Поточна вартість одиниці є зворотною величиною відносно майбутньої вартості, тому процес її визначення називають дисконтуванням, а її розрахунки для суми FV ведуться за формулою:
Величину Дана функція надає можливість визначити теперішню вартість суми, якщо відома її майбутня величина, період, за який цю суму накопичено, та процента ставка. Графічна інтерпретація функції дисконтування наведена на рис. 5.2.
Рис. 5.2. Поточна вартість одиниці Приклад. Яку суму сьогодні необхідно депонувати в банк під 20 % річних із щоквартальним нарахуванням відсотків для того, щоб через рік мати змогу придбати у власність бізнес вартістю 100 тис. грн.? Поточну вартість визначимо за формулою (5.4):
Таким чином, щоб отримати можливість через рік стати власником бізнесу вартістю 100 тис. грн., сьогодні необхідно депонувати в банк під 20 % річних із щоквартальним нарахуванням відсотків 82,27 тис. грн. 3. Поточна вартість аннуітету. Оскільки аннуітет становить собою особливий грошовий потік, представлений однаковими сумами через однакові часові інтервали, то відносно інвестора він може бути як вихідним (наприклад, здійснення періодичних однакових платежів), так і вхідним грошовим потоком (наприклад, регулярні надходження фіксованих сум орендної плати). Крім того, залежно від моменту здійснення першого аннуітетного платежу розрізняють звичайний та авансовий аннуітет. Звичайний аннуітет визначається як сума рівновеликих платежів, що здійснюються наприкінці періоду. Авансовий аннуітет має місце за умов часового збігу першого платежу з депонуванням основної суми внеску. Графічна інтерпретація поточної вартості звичайного аннуітету наведена на рис. 5.3:
Рис. 5.3. Поточна вартість звичайного аннуітету
Формула для розрахунку звичайного аннуітету має вигляд:
де PVA – поточна вартість аннуітету; А – платіж n -го періоду. Множник Приклад. Власник підприємства планує придбати нове обладнання для виробничого підрозділу через 3 роки. На сьогоднішній день вартість такого обладнання оцінюється в 35000 грн. Чи вистачить у власника коштів на переобладнання цеху, якщо він вкладатиме наприкінці кожного кварталу 4500 грн. на рахунок під 24 % річних? Розрахуємо поточну вартість щоквартальних аннуітетних платежів в 4500 грн. під 24 % річних за формулою (5.5):
Таким чином, щоквартальних внесків у 4500 грн. під 24 % річних вистачить власнику для придбання нового обладнання через 3 роки (37727,3 > 35000). Графічна інтерпретація поточної вартості авансового аннуітету наведена на рис. 5.4:
Рис. 5.4. Поточна вартість авансового аннуітету
Для того, щоб розрахувати поточну вартість авансового аннуітету, необхідно дослідити рух грошового потоку. Оскільки перший платіж збігається за часом із депонуванням основної суми внеску, то його майбутня вартість дорівнює теперішній і не потребує дисконтування для забезпечення порівнянності. Всі наступні аннуітетні платежі дисконтуються в звичайному порядку, проте період дисконтування завжди буде на одиницю менше. Тому фактор поточної вартості авансового аннуітету дорівнює фактору поточної вартості звичайного аннуітету для попереднього періоду, збільшеному на одиницю. Формула для розрахунку авансового аннуітету має вигляд:
Приклад. Розрахувати поточну вартість орендних платежів, які здійснюються щорічно на початку розрахункового періоду в 5 років. Сума щорічного орендного платежу дорівнює 20 тис. грн., ставка дисконту – 10 %. Поточна вартість орендних платежів за 5 років за формулою (5.6) становитиме:
Зміни, що відбуваються у зовнішньому середовищі, а також розвиток внутрішнього потенціалу підприємства чинять суттєвий вплив на величину періодичного грошового потоку доходів. Тому на практиці досить часто трапляються ситуації, коли за визначений розрахунковий період величина періодичних платежів змінюється, що вимагає застосування певних методичних прийомів розрахунку поточної вартості таких аннуітетних платежів. Приклад. Експлуатація готельного комплексу забезпечує отримання щорічного доходу в розмірі 120 тис. грн. протягом 4 років і в розмірі 150 тис. протягом наступних 3 років. Якою буде поточна вартість доходів за 7 років, якщо ставка дисконту 9 %? В даному випадку існує декілька варіантів розрахунків:
Рис. 5.5. Поточна вартість мінливого потоку доходів (1 варіант)
За перші 4 роки поточну вартість доходів розрахуємо за формулою (5.5):
Фактор поточної вартості аннуітету за останні три роки дорівнює різниці факторів, що відповідають кінцевому та початковому періодам виникнення збільшеної суми доходів відносно поточного (нульового) періоду. За таких умов поточна вартість доходів за останні три роки становитиме:
Загальна поточна вартість доходів за 7 років дорівнює 657,75 тис. грн. (388,77 + 268,98). 2) Поточна вартість загальної суми доходів за 7 років дорівнює різниці поточної вартості доходів в 150 тис. грн. за всі 7 років та поточної вартості неіснуючих доходів в 30 тис. грн. (150 – 120) за перші 4 роки (рис. 5.6).
Рис. 5.6. Поточна вартість мінливого потоку доходів (2 варіант)
Поточна вартість доходів в 150 тис. грн., виходячи з припущення, що вони надходять протягом усіх 7 років, дорівнює:
Поточна вартість неіснуючих доходів в 30 тис. грн, які виникли протягом перших 4 років, дорівнює:
Поточна вартість загальної суми доходів за 7 років становитиме:
754,94 – 97,19 = 657,75 (тис. грн).
3) За цим варіантом поточна вартість загальної суми доходу за 7 років дорівнює сумі поточній вартості доходу в 120 тис. грн. за 7 років та поточної вартості величини перевищення в 30 тис. грн., на яку зросли доходи за останні 3 роки (рис. 5.7).
Рис. 5.7. Поточна вартість мінливого потоку доходів (3 варіант)
Поточна вартість доходів в 120 тис. грн., виходячи з припущення, що вони надходять протягом усіх 7 років, дорівнює:
Поточна вартість величини перевищення доходів в 30 тис. грн, які виникали протягом останніх 3 років, дорівнює:
Поточна вартість загальної суми доходів за 7 років становитиме:
603,95 + 53,8 = 657,75 (тис. грн).
4. Періодичний внесок на погашення позики (внесок на амортизацію одиниці) Ця функція виступає зворотною відносно поточної вартості аннуітету і використовується для розрахунку фіксованої суми аннуітетного платежу, якщо відомі його поточна вартість, кількість внесків і ставка дисконту. Під амортизацією в даному випадку розуміють процес погашення боргу за визначений період часу. Графічна інтерпретація розрахунків періодичного внеску на погашення позики наведена на рис. 5.8.
Рис. 5.8. Періодичний внесок на погашення позики
Розрахунок періодичного внеску на погашення позики (амортизацію одиниці) здійснюється за формулою:
Множник Приклад. Вартість нерухомості дорівнює 1500 тис. грн. Для її придбання було залучено позику в розмірі 70 % від вартості нерухомості під 14 % річних із погашенням кожні півроку протягом 3 років. Розрахувати залишок заборгованості за основною сумою позики через 2 роки. Розрахуємо величину періодичного внеску на погашення позики за півріччя за формулою (5.7):
Залишок заборгованості за основною сумою позики через 2 роки розрахуємо за допомогою методу депозитної книжки [47]. Логіка розрахунків за даним методом така: поточна вартість аннуітету – це величина депозиту плюс загальна сума нарахованих процентів, яка щорічно зменшується на рівні суми. Сума щорічного платежу складається із нарахованих за цей рік процентів і частини основної суми боргу. Структура річного платежу постійно змінюється – на початку періоду в ньому переважають нараховані проценти за черговий період, наприкінці періоду частка процентів зменшується та зростає частка повернення основної суми боргу. Розрахунки залишку заборгованості за основною сумою позики за прикладом, що розглядається, наведено в таблиці 5.1.
Таблиця 5.1 – Розрахунок залишку заборгованості за методом депозитної книжки
Таким чином, через два роки сума заборгованості за позикою складатиме 239377,1 грн. 5. Майбутня вартість аннуітету (зростання одиниці за період) Використання цієї функції доцільно за умов визначення майбутньої вартості суми, яку буде накопичено за рахунок надходження аннуітетних платежів при заданій процентній ставці (рис. 5.9).
Рис. 5.9. Майбутня вартість аннуітету
Розрахунок майбутньої вартості звичайного аннуітету здійснюється за формулою:
де FVA – майбутня вартість аннуітету. Множник Приклад. Підприємець планує придбати офісне приміщення через 2 роки. Вартість аналогічного приміщення сьогодні оцінюється в 120000 грн. і прогнозується її збільшення на 5 % щорічно. Чи вистачить у підприємця коштів на придбання офісу, якщо він вкладатиме наприкінці кожного року 50000 грн. на рахунок під 15 % річних? Слід зазначити, що розрахунки необхідної суми коштів можуть відбуватися за двома напрямками: з використанням функції поточної вартості аннуітету (об’єктами порівняння в цьому разі мають бути сьогоднішня вартість аналогічного офісу та поточна вартість аннуітетних платежів) та з використанням функції майбутньої вартості аннуітету. В останньому випадку порівнюватися мають майбутня вартість офісного приміщення через 2 роки та майбутня вартість аннуітетного внеску під 15 % річних. Для ілюстрації розрахунків майбутньої вартості аннуітету розглянемо другий напрямок. На першому етапі розрахуємо вартість офісного приміщення через два роки за формулою (5.1):
Наступним етапом є розрахунок майбутньої вартості щорічних аннуітетних внесків у розмірі 50000 грн. під 15 % річних за формулою (5.8):
Таким чином, щорічні внески у розмірі 60000 грн. під 15 % річних не забезпечуть нагромадження необхідної суми для придбання офісу через 2 роки (129000 < 137812,5). Для авансового аннуітету розрахункова формула майбутньої вартості має вигляд:
Приклад. Щомісячні орендні платежі надходять на початку кожного місяця у розмірі 12000 грн. Середньоринкова місячна ставка доходу – 6 %. Якою буде майбутня вартість платежів наприкінці 8-го місяця? Розрахунок майбутньої вартості авансового аннуітету в розмірі 12000 грн. здійснюємо за формулою (5.9):
6. Періодичний внесок до фонду нагромадження (фактор фонду відшкодування). Дана функція є зворотною відносно майбутньої вартості аннуітету та дозволяє визначити розмір грошового внеску, який слід періодично депонувати на рахунок, щоб через певний часу мати необхідну суму коштів при заданій ставці дисконту (рис. 5.10). Формула для розрахунку періодичного внеску до фонду нагромадження має вигляд:
Рис. 5.10. Періодичний внесок до фонду нагромадження
Множник Приклад. Розрахувати суму щорічного внеску на банківський рахунок під 11 % річних для придбання нової технологічної лінії вартістю 45000 грн. через 3 роки? Розрахунок періодичного внеску до фонду нагромадження здійснюємо за формулою (5.10):
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 711; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.198.150 (0.011 с.) |

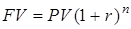 (5.1)
(5.1) називають фактором майбутньої вартості або фактором накопичення. Його значення для різних r та n містяться в колонці 2 фінансових таблиць додатку 1.
називають фактором майбутньої вартості або фактором накопичення. Його значення для різних r та n містяться в колонці 2 фінансових таблиць додатку 1.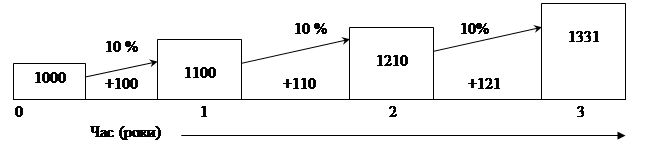
 = 150 × 1,7623 = 264,35 (тис. грн).
= 150 × 1,7623 = 264,35 (тис. грн). (5.2)
(5.2)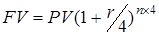 (5.3)
(5.3)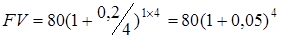 = 80 × 1,2155 = 97,24 (тис. грн)
= 80 × 1,2155 = 97,24 (тис. грн)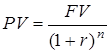 (5.4)
(5.4) називають дисконтним множником або фактором поточної вартості. Його значення для різних r та n містяться в кол. 3 фінансових таблиць додатку 1.
називають дисконтним множником або фактором поточної вартості. Його значення для різних r та n містяться в кол. 3 фінансових таблиць додатку 1.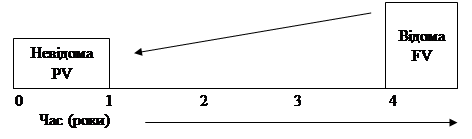
 100 × 0,8227 = 82,27 (тис. грн).
100 × 0,8227 = 82,27 (тис. грн).
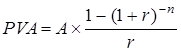 (5.5)
(5.5) називають дисконтним множником аннуітету, фактором поточної вартості аннуітету або фактором Інвуда. Його значення для різних r та n містяться в кол. 4 фінансових таблиць додатку 1.
називають дисконтним множником аннуітету, фактором поточної вартості аннуітету або фактором Інвуда. Його значення для різних r та n містяться в кол. 4 фінансових таблиць додатку 1.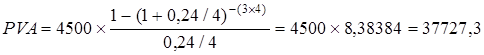 грн.
грн.
 (5.6)
(5.6) (тис.грн)
(тис.грн) 1) Поточна вартість доходів за 7 років дорівнює сумі поточної вартості доходів в 120 тис. грн. за перші 4 роки та поточної вартості доходів в 150 тис. грн. за наступні 3 роки (рис. 5.5).
1) Поточна вартість доходів за 7 років дорівнює сумі поточної вартості доходів в 120 тис. грн. за перші 4 роки та поточної вартості доходів в 150 тис. грн. за наступні 3 роки (рис. 5.5). = 120 × 3,23972 = 388,77 (тис. грн)
= 120 × 3,23972 = 388,77 (тис. грн) = 150 × (5,03295 – 3,23972) = = 268,98 (тис. грн).
= 150 × (5,03295 – 3,23972) = = 268,98 (тис. грн).
 = 150 × 5,03295 = 754,94 (тис. грн).
= 150 × 5,03295 = 754,94 (тис. грн). = 30 × 3,23972 = 97,19 (тис. грн).
= 30 × 3,23972 = 97,19 (тис. грн).
 = 120 × 5,03295 = 603,95 (тис. грн).
= 120 × 5,03295 = 603,95 (тис. грн).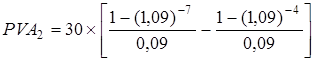 =30× (5,03295–3,23972) = 53,8 (тис. грн).
=30× (5,03295–3,23972) = 53,8 (тис. грн).
 (5.7)
(5.7)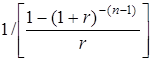 називається фактором внеску на амортизацію одиниці або фактором внеску на погашення позики. Його значення для різних r та n містяться в кол. 5 фінансових таблиць додатку 1.
називається фактором внеску на амортизацію одиниці або фактором внеску на погашення позики. Його значення для різних r та n містяться в кол. 5 фінансових таблиць додатку 1.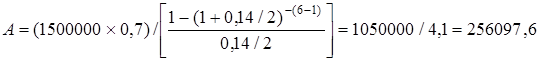 (грн.)
(грн.)
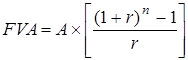 , (5.8)
, (5.8) називається фактором майбутньої вартості аннуітету. Його значення для різних r та n містяться в кол. 6 фінансових таблиць додатку 1.
називається фактором майбутньої вартості аннуітету. Його значення для різних r та n містяться в кол. 6 фінансових таблиць додатку 1.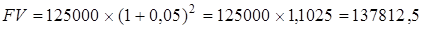 грн.
грн. = 60000 × 2,15 = 129000 (грн.)
= 60000 × 2,15 = 129000 (грн.) . (5.9)
. (5.9) = 12000 × 9,89747 × 1,06 = = 125895,8 (грн)
= 12000 × 9,89747 × 1,06 = = 125895,8 (грн)
 (5.10)
(5.10) називається фактором періодичного внеску до фонду нагромадження або фактором внеску до фонду відшкодування. Його значення для різних r та n містяться в кол. 7 фінансових таблиць додатку 1.
називається фактором періодичного внеску до фонду нагромадження або фактором внеску до фонду відшкодування. Його значення для різних r та n містяться в кол. 7 фінансових таблиць додатку 1.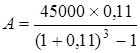 = 45000 × 0,29921 = 13464,5 (грн.).
= 45000 × 0,29921 = 13464,5 (грн.).


