
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні способи множення чисел у прямих кодахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При множенні чисел у прямих кодах знакові та основні розряди обробляються окремо. Для визначення знака добутку здійснюють підсумовування по модулю 2 цифр, що розміщуються в знакових розрядах співмножників. Будемо вважати, що множене Y та множник Х – правильні двійкові дроби вигляду
Множення двох чисел Y та Х може бути реалізоване шляхом виконання визначеного циклічного процесу, характер якого залежить від конкретної форми виразу (1.1). Один цикл множення складається з додавання чергового часткового добутку, що являє собою добуток множеного на одну цифру множника, до суми часткових добутків. Розрізняють чотири способи множення. Перший спосіб Вираз (1.1) можна подати у вигляді:
з отриманого виразу виходить, що отримання суми часткових добутків в i -му циклі, де
з початковими значеннями В розглянутому способі множення здійснюється з молодших розрядів множника, сума часткових добутків зсувається вправо, а множене залишається нерухомим. Другий спосіб Подамо вираз (1.1) у наступному вигляді:
Очевидно, що процес множення може бути зведений до n -кратного виконання циклу
з початковими значеннями У розглянутому способі множення здійснюється з молодших розрядів, множене зсувається вліво, а сума часткових добутків залишається нерухомою. Третій спосіб Подамо вираз (1.1) у наступному вигляді:
Суму часткових добутків у i -му циклі
з початковими значеннями У розглянутому способі множення здійснюється зі старших розрядів множника, сума часткових добутків зсувається вліво, а множене нерухоме. Четвертий спосіб Подамо вираз (1.1) у наступному вигляді:
В цьому випадку процес множення може бути зведений до n -кратного виконання циклу
с початковими значеннями У розглянутому способі множення виконується зі старших розрядів множника, сума часткових добутків залишається нерухомою, а множене зсувається вправо. Для формування і накопичення суми часткових добутків можна використовувати або комбінаційний суматор (SM) і регістр добутку, або тільки накопичувальний суматор, який у функціональному відношенні можна розглядати як композицію комбінаційного суматора і регістра. Принцип побудови пристроїв, що реалізують різні способи множення, показаний на рис. 1.1, де RG 3 – регістр множеного, RG 1 – регістр добутку, RG 2 – регістр множника. Цифрами зазначені номери розрядів SM і регістрів, а стрілками показаний напрямок зсуву кодів у регістрах. Цифри, що записані в молодших розрядах регістрів RG 3 і RG 1, при реалізації першого способу мають вагу При множенні першим способом (рис. 1.1, а) в першому такті i -го циклу аналізується значення RG 2 (n) - молодшого (n -го) розряду регістру RG 2, в якому знаходиться чергова цифра множника. Вміст RG 3 додається до суми часткових добутків, що знаходяться в регістрі RG1, якщо RG 2 (n) =1, або не додається, якщо RG 2 (n) =0. В другому такті здійснюється правий зсув в регістрах RG 1 і RG 2, що еквівалентно множенню їх вмісту на Час множення, якщо не застосовуються методи прискорення операції, визначається виразом
а б
в г Рис. 1.1. Операційні схеми пристроїв для множення чисел: а – перший спосіб; б – другий спосіб; в – третій спосіб; г – четвертий спосіб Перед початком множення другим способом (рис. 1.1, б) множник Х записують в регістр RG 2, а множене Y – в молодші розряди регістру RG 3 (тобто в регістрі RG 3 установлюють При множенні третім способом (рис. 1.1, в) вага молодшого розряду RG 3 дорівнює Перед множенням четвертим способом (рис. 1.1, г) множник записують в регістр RG 2, а множене – в старші розряди регістру RG 3 (тобто в RG 3 установлюють Y 0= Y 2-1). В кожнім циклі цифра RG 2(1), що знаходиться в старшому розряді регістру RG 2, керує підсумовуванням, а в RG 3 здійснюється правий зсув на один розряд, що еквівалентно множенню вмісту цього регістра на 2-1. Час виконання множення четвертим способом складає В ЕОМ при роботі з дробовими числами часто потрібно обчислювати не 2 n, а тільки (n +1) цифр добутку й округляти його до n розрядів. В цьому випадку при реалізації другого способу можна зменшити довжину SM і RG 1, а при реалізації четвертого – зменшити довжину SМ, RG 1 і RG 3. Для того, щоб похибка від відкидання молодших розрядів не перевищила половини ваги n -го розряду результату, в перерахованих вузлах досить мати тільки по l додаткових молодших розрядів, де l вибирається з умови
Операція округлення здійснюється звичайно шляхом додавання одиниці до n +1-го розряду результату і відкидання всіх розрядів, розташованих правіше n -го. При цьому похибка стає знакозмінною, а максимальне абсолютне її значення не перевищує половини ваги молодшого розряду. Додаткового такту підсумовування для округлення не потрібно. Досить записати одиницю перед початком множення в той розряд регістру RG 1, що після виконання множення залишається старшим розрядом, який відкидається. У процесі формування суми часткових добутків код з регістру RG 1 видається на суматор SM, а з виходів SM знову записується в регістр RG 1. У зв'язку з цим при використанні потенційних елементів регістр RG 1 будують на тригерах із внутрішньою затримкою. Характер керуючих сигналів і ланцюга, на який вони впливають, визначається конкретною теоретичною реалізацією вузлів і використовуваною елементною базою. У операційних пристроях, що реалізують другий і четвертий способи множення, можна без пересилань кодів між регістрами обчислювати вирази вигляду У операційному пристрої, що реалізує третій спосіб, можна без пересилань обчислювати, наприклад, функції вигляду Хi. Для цього множник Х перед початком обчислення записується в регістр RG 3 і в молодші розряди регістру RG 2, а потім (і –1) раз виконується операція множення з округленням проміжних результатів до n розрядів. Після кожної чергової операції регістр RG 1 встановлюється в нульовий стан. Остаточний результат буде знаходитися в n молодших розрядах регістру RG 2. Найбільш простими є пристрої, що реалізують перший спосіб, а найбільш швидкодіючими – другий і четвертий. Однак другий спосіб не має особливих переваг порівняно з четвертим і, крім того, вимагає великих апаратурних витрат при реалізації. Арифметико-логичні пристрої Арифметико-логічні пристрої (АЛП) призначені для виконання арифметичних та логічних операцій над машинними словами (числами, командами та машинними кодами інших об'єктів). За структурою АЛП розрізняють: – АЛП з розподіленою логікою (інакше називають АЛП із закріпленими мікроопераціями). Апаратура для реалізації мікрооперацій розподілена між регістрами та закріплена за ними, тобто кожен регістр використовує власну логіку для виконання мікрооперацій (МО); – АЛП із зосередженою логікою (інакше називають АЛП із загальними МО). У таких пристроях всі логічні ланцюги об'єднані в арифметико-логічному блоці (АЛБ), Всі регістри реалізовані у вигляді надоперативного запам’ятовуючого пристрою (НОЗП).
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 818; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.188.174 (0.007 с.) |

 ,
,  , де
, де  . Тоді добуток Z абсолютних величин чисел Y та X дорівнює
. Тоді добуток Z абсолютних величин чисел Y та X дорівнює . (1.1)
. (1.1)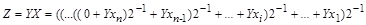 ,
, , зводиться до обчислення виразу
, зводиться до обчислення виразу
 , причому
, причому  .
.
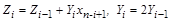
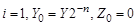 .
.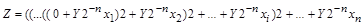 .
. ,
, .
.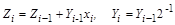
 .
. , а при реалізації інших способів –
, а при реалізації інших способів –  . Перед початком множення будь-яким способом регістр RG1 встановлюється в нульовий стан. Підрахунок кількості циклів множення забезпечують лічильники СТ, відповідно з чим обирається його розрядність q.
. Перед початком множення будь-яким способом регістр RG1 встановлюється в нульовий стан. Підрахунок кількості циклів множення забезпечують лічильники СТ, відповідно з чим обирається його розрядність q. . При зсуві цифра молодшого розряду регістру RG 1 записується у вивільнюваний старший розряд регістру RG 2. Після виконання n циклів молодші розряди 2 n -розрядного добутку будуть записані в регістр RG 2, а старші – у RG 1.
. При зсуві цифра молодшого розряду регістру RG 1 записується у вивільнюваний старший розряд регістру RG 2. Після виконання n циклів молодші розряди 2 n -розрядного добутку будуть записані в регістр RG 2, а старші – у RG 1. , де
, де  і
і 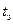 –тривалості тактів підсумовування і зсуву відповідно.
–тривалості тактів підсумовування і зсуву відповідно.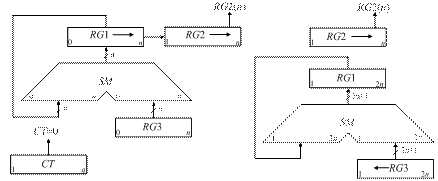

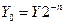 ). В кожному i -му циклі множення додаванням кодів RG 3 і RG 1 керує цифра RG 2(n), а в регістрі RG 3 здійснюється зсув вліво на один розряд, в результаті чого формується величина
). В кожному i -му циклі множення додаванням кодів RG 3 і RG 1 керує цифра RG 2(n), а в регістрі RG 3 здійснюється зсув вліво на один розряд, в результаті чого формується величина  . Оскільки сума часткових добутків в процесі множення нерухома, зсув в регістрі RG3 можна сполучити в часі з підсумовуванням (як правило,
. Оскільки сума часткових добутків в процесі множення нерухома, зсув в регістрі RG3 можна сполучити в часі з підсумовуванням (як правило,  ). В цьому випадку
). В цьому випадку  . Завершення операції множення визначається за нульовим вмістом регістру RG 2, що також приводить до збільшення швидкодії, якщо множник ненормалізований.
. Завершення операції множення визначається за нульовим вмістом регістру RG 2, що також приводить до збільшення швидкодії, якщо множник ненормалізований. . На початку кожного циклу множення здійснюється лівий зсув в регістрах RG 1 і RG 2, а потім виконується додавання, яким керує RG 2(1). В результаті підсумовування вмісту RG 3 і RG 1 може виникнути перенос в молодший розряд регістру RG 2. У старшій частині суматора, на якому здійснюється підсумовування коду RG 2 з нулями, відбувається поширення переносу. Збільшення довжини RG 2 на один розряд усуває можливість поширення переносу в розряди множника. Після виконання n циклів молодші розряди добутку будуть знаходитися в регістрі RG 1, а старші – в регістрі RG 2. Час множення третім способом визначається аналогічно першому способу і дорівнює
. На початку кожного циклу множення здійснюється лівий зсув в регістрах RG 1 і RG 2, а потім виконується додавання, яким керує RG 2(1). В результаті підсумовування вмісту RG 3 і RG 1 може виникнути перенос в молодший розряд регістру RG 2. У старшій частині суматора, на якому здійснюється підсумовування коду RG 2 з нулями, відбувається поширення переносу. Збільшення довжини RG 2 на один розряд усуває можливість поширення переносу в розряди множника. Після виконання n циклів молодші розряди добутку будуть знаходитися в регістрі RG 1, а старші – в регістрі RG 2. Час множення третім способом визначається аналогічно першому способу і дорівнює 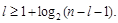
 , де (
, де ( ) для чого досить черговий результат операції залишати в регістрі RG 2, який в цьому випадку повинен мати додаткові старші розряди.
) для чого досить черговий результат операції залишати в регістрі RG 2, який в цьому випадку повинен мати додаткові старші розряди.


