
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Относительность движения. Система отсчёта. Сложение перемещений и скоростей, переход в другие системы отсчетаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Начальный уровень: А1. На столике в вагоне движущегося поезда лежит книга. Относительно каких тел книга находится в покое: а) столика; б) рельсов; в) пола вагона? А2. С полки равномерно движущегося вагона падает яблоко. Какова траектория яблока относительно наблюдателя, стоящего на перроне? Изобразите траекторию на рисунке. А3. Гайка свинчивается с неподвижного болта. Изобразите примерно траекторию точки на поверхности гайки относительно болта. А4. Одинаковые ли пути проходят электровоз и последний вагон поезда? А5. Корабль подплывает к пристани. Относительно каких тел пассажиры, стоящие на палубе этого корабля, находятся в движении: а) реки; б) палубы корабля; в) берега? А6. (29.Р) Может ли человек, находясь на движущемся эскалаторе метро, быть в покое в системе отсчета, связанной с землей? А7. (1.Т) Стратонавты рассказывают, что если не обращать внимания на показания приборов невозможно определить, поднимается или опускается ли вообще стратостат. Чем это объясняется? А8. (2.Т) Какие части катящегося вагона движутся и какие находятся в покое относительно дороги, стен вагона? А9. (3.Т) Мимо стоящего автомобиля проезжает колонна движущихся с одинаковой скоростью тракторов. Движется ли каждый из тракторов относительно автомобиля? Движется ли трактор относительно другого трактора? Движется ли автомобиль относительно трактора? А10. (7.Т)Почему говорят, что Солнце восходит и заходит? Что в данном случае является телом отсчета? А11. (14.Т) Пассажир скорого поезда смотрит в окно на вагоны встречного поезда. В момент, когда последний вагон встречного поезда прошел мимо его окна, пассажир ощутил, что его движение резко замедлилось. Почему? А12. (17.Т) Почему дождевые капли в безветренную погоду оставляют наклонные прямые полосы на стеклах равномерно движущегося железнодорожного вагона? А13. (19.Т) При каких условиях летчик реактивного истребителя может рассмотреть пролетающий недалеко от него артиллерийский снаряд? А14. (21.Т) В кинофильме «Снова к звездам» показана тренировка космонавта-2 Г. С. Титова в беге на движущейся ленте пола. Каким образом можно определить скорость бега, если Г. С. Титов не пробегал ни одного метра относительно стен зала? Средний уровень: Б1. (26.Т) Будет ли слушаться руля легкая лодка, свободно несущаяся по течению реки? Б2. (4.Т) Какова траектория движения точек винта самолета по отношению к летчику? по отношению к земле? Б3. (15.Т) Четырехугольная платформа движется по рельсам. Человек идет по диагонали платформы. За время передвижения человека из угла в угол платформа смещается по рельсам на расстояние, равное трем ее корпусам. Изобразите вектор перемещения человека относительно Земли. Б4. Нарисуйте приблизительно траекторию движения какой-либо точки обода катящегося колеса относительно дороги, рамы велосипеда и относительно оси вращения.
Б6. (8.Т) Чему равно перемещение какой-либо точки, находящейся на краю диска радиусом R при его повороте относительно подставки на 60°? на 180°? (Решить задачу в системах отсчета, связанных с подставкой и диском.) Б7. (1.К) Два автомобиля движутся навстречу друг другу со скоростями 90 км/ч и 60 км/ч относительно земли. Определите модуль скорости первого автомобиля относительно второго. Б8. (2.К) Два поезда движутся в одном направлении со скоростями 70 км/ч и 50 км/ч относительно земли. Определите: а) модуль скорости первого поезда относительно второго; б) модуль скорости второго поезда относительно первого. Б9. (3.К) Скорость первого автомобиля относительно второго 110 км/ч. Определите скорость второго автомобиля относительно земли, если скорость первого относительно земли - 70 км/ч. Автомобили движутся навстречу друг другу. Б10. (4.К) Скорость первого автомобиля относительно второго 30 км/ч, а относительно земли - 120 км/ч. Определите модуль скорости второго автомобиля относительно земли, если автомобили движутся в одном направлении. Б11. (5.К) Велосипедист едет со скоростью 36 км/ч. Скорость ветра 2 м/с. Определите скорость ветра относительно велосипедиста, если: а) ветер встречный; б) ветер попутный. Б12. (1.18Г) Танк движется со скоростью 72 км/ч. С какой скоростью движутся относительно Земли: а) верхняя часть гусеницы; б) нижняя часть гусеницы; в) точка гусеницы, которая в данный момент движется вертикально по отношению к танку? Б13. (6.К) Сколько времени пассажир, сидящий у окна поезда, который идет со скоростью 54 км/ч, будет видеть проходящий мимо него встречный поезд, скорость которого 36 км/ч, длина поезда 250 м. Б14. (33.Р) Два поезда движутся навстречу, друг другу со скоростями 72 и 54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда? Б15. (1.8Г) Колонна войск во время похода движется со скоростью v1 = 5 км/ч, растянувшись по дороге на расстояние L - 400 м. Командир, находящийся в хвосте колонны, посылает велосипедиста с поручением головному отряду. Велосипедист отправляется и едет со скоростью v2 = 25 км/ч и, на ходу выполнив поручение, сразу же возвращается обратно с той же скоростью. Через сколько времени t после получения поручения он вернулся обратно? Б16. (7.К) Скорость течения реки 2 км/ч. Моторная лодка идет против течения со скоростью 15 км/ч (относительно берега). С какой скоростью она будет двигаться по течению (относительно берега и относительно воды)? Б17. (8.К) Скорость лодки относительно воды 4 км/ч, а скорость течения 2 км/ч. За какое время лодка пройдет 12 км по течению реки? Против течения? Б18. (18.Т) Эскалатор метро движется вверх со скоростью 0,75 м/сек. а) С какой скоростью и в каком направлении надо идти по эскалатору, чтобы быть все время на уровне одного из фонарей освещения туннеля? б) С какой скоростью относительно поднимающейся лестницы надо было бы передвигаться, чтобы опускаться вниз со скоростью пассажиров, неподвижно стоящих на другой опускающейся лестнице? Б19. (32.Р) Эскалатор метро движется со скоростью 0,75 м/с. Найти время, за которое пассажир переместится на 20 м относительно земли, если он сам идет в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета, связанной с эскалатором. Б20. (40.Р) Скорость продольной подачи резца токарного станка 12 см/мин, а поперечной подачи 5 см/мин. Какова скорость резца в системе отсчета, связанной с корпусом станка? Б21. (41.Р) Вертолет летел на север со скоростью 20 м/с. С какой скоростью и под каким углом к меридиану будет лететь вертолет, если подует западный ветер со скоростью 10 м/с? Б22. (1.9Г) Вагон шириной d = 2,4 м, движущийся со скоростью v = 15 м/с, был пробит пулей, летевшей перпендикулярно движению вагона. Смещение отверстий в стенках вагона относительно друг друга равно 1 = 6 см. Какова скорость движения пули? Б23. (23.Т) По реке плывет весельная лодка и рядом с ней плот. Что легче для гребца: перегнать плот на 10 м или на столько же отстать от него? Б24. (24.Т) Пролетая над пунктом А, пилот вертолета догнал воздушный шар, который сносило ветром по курсу вертолета. Через полчаса пилот повернул назад и встретил воздушный шар на расстоянии 30 км от пункта А. Какова скорость ветра, если двигатель вертолета работал, не меняя мощности? Б25. (28.Т) По гладкому горизонтальному столу со скоростью V1 движется лист закопченного стекла. Какой формы след оставит на стекле шарик, брошенный по поверхности листа со скоростью относительно стола V2 перпендикулярно направлению движения листа? Задачу решить графически. Б26. (29.Т) Самолет пролетает над железной дорогой, по которой идет поезд со скоростью v1. Скорость самолета v2 направлена перпендикулярно к железной дороге. Определите графически скорость поезда v относительно самолета. Достаточный уровень: В1. (6.Т) Из центра горизонтально расположенного вращающегося диска по его поверхности пущен шарик. Каковы траектории шарика относительно Земли и диска? В2. (16.Т) Может ли при сложении двух скоростей по правилу параллелограмма скорость сложного движения быть численно равной одной из составляющих скоростей? Меньше меньшей составляющей скорости? В3. (31.Р) Гусеничный трактор Т 150 движется с максимальной скоростью 18 км/ч. Найти проекции векторов скоростей верхней и нижней части гусеницы на оси X и X1. Ось X связана с землей, а ось X1 — с трактором. Обе оси направлены по ходу движения трактора. В4. (1.К) Расстояние между пунктами А и Б равно 250 км. Одновременно из обоих пунктов навстречу друг другу выезжают два автомобиля. Автомобиль, выехавший из пункта А, движется со скоростью 60 км/ч, а выехавший из пункта В — со скоростью 40 км/ч. Через какое время и на каком расстоянии от пункта А встретятся автомобили? В5. (2.К) От станции отошел товарный поезд, идущий со скоростью 36 км/ч. Через 0,5 ч в том же направлении вышел скорый поезд, скорость которого 72 км/ч. Через какое время после отправления скорого поезда он догонит товарный? В6. (3.К) Из городов А и В, расстояние между которыми 120 км, одновременно выехали навстречу друг другу две автомашины со скоростями 20 км/ч и 60 км/ч. Через какое время и на каком расстоянии от города С, находящегося на полпути между А и В, встретятся автомобили? В7. (4.К) Из двух пунктов, расстояние между которыми 100 м, одновременно навстречу друг другу начали двигаться два тела. Скорость одного из них 20 м/с. Какова скорость второго тела, если они встретились через 4 с? В8. (5.К) От пристани А до пристани Б моторная лодка шла 6 ч, а обратно — 3 ч. Скорость лодки относительно воды оставалась все время одной и той же. За какое время проплывает эта лодка от Б до А с выключенным мотором? В9. (1.6Г) Между двумя пунктами, расположенными на реке на расстоянии 100 км один от другого, курсирует катер, который, идя по течению, проходит это расстояние за время 4 ч, а против течения — за время 10 ч. Определить скорость течения реки и скорость v катера относительно воды. В10. (6.К) Эскалатор поднимает стоящего человека за 1 минуту. Если человек поднимается по неподвижному эскалатору, то на это уходит 3 минуты. Сколько времени понадобится на подъем, если человек будет идти по движущемуся эскалатору? В11. (1.4Г) Эскалатор метро спускает идущего по нему вниз человека за 1 мин. Если человек будет идти вдвое быстрее, то он спустится за 45 с. Сколько времени спускается человек, стоящий на эскалаторе? В12. (1.5Г) Человек бежит по эскалатору. В первый раз он насчитал n1 = 50 ступенек, во второй раз, двигаясь в ту же сторону со скоростью втрое большей, он насчитал n2 = 75 ступенек. Сколько ступенек он насчитал бы на неподвижном эскалаторе? В13. (7.К) От пристани А одновременно отчаливают плот и катер. Катер доплывает до пристани Б и, сразу же повернув обратно, возвращается в А. Какую часть пути от А до Б проплывет за это время плот, если скорость катера относительно воды в 4 раза больше скорости течения? В14. (8.К) Человек, идущий вниз по опускающемуся эскалатору, затрачивает на спуск 1 минуту. Если человек будет идти вдвое быстрее, он затратит на 15 секунд меньше. Сколько времени он будет опускаться, стоя на эскалаторе? В15. (9.К) Моторная лодка проходит расстояние между двумя пунктами А и В по течению реки за 3 часа, а плот — за 12 часов. Какое время моторная лодка затратит на обратный путь? В16. (10.К) Самолет летит из пункта А в пункт В и обратно со скоростью 300 км/ч относительно воздуха. Расстояние между пунктами А и В равно 900 км. Сколько времени затратит самолет на весь полет, если вдоль линии полета непрерывно дует ветер со скоростью 60 км/ч? В17. (11.К) Моторная лодка движется по реке от пункта А до пункта В 4 часа, а обратно — 5 часов. Какова скорость течения реки, если расстояние между пунктами 80 км? В18. (34.P) Скорость движения лодки относительно воды в n раз больше скорости течения реки. Во сколько раз больше времени занимает поездка на лодке между двумя пунктами против течения, чем по течению? Решить задачу для значений n = 2 и n = 11. В19. (42.Р) Катер, переправляясь через реку, движется перпендикулярно течению реки со скоростью 4 м/с в системе отсчета, связанной с водой. На сколько метров будет снесен катер течением, если ширина реки 800 м, а скорость течения 1 м/с?
В21. (44.Р) Моторная лодка, имеющая в системе отсчета, связанной с водой, скорость 6 м/с, должна переправиться через реку по кратчайшему пути. Какой курс относительно берега необходимо держать при переправе, Рис.В20 если скорость течения реки 2 м/с? Задачу решить графически. Какова скорость лодки относительно земли? В22. (45.Р) В безветренную погоду вертолет двигался со скоростью 90 км/ч точно на север. Найти скорость и курс вертолета, если подул северо-западный ветер под углом 45° к меридиану. Скорость ветра 10 м/с. Задачу решить графически. В23. (1.12Г) С какой скоростью v и по какому курсу должен лететь самолет, чтобы за время t = 2 ч пролететь точно на Север путь S = 300 км, если во время полета дует северо-западный ветер под углом α = 30° к меридиану со скоростью u = 27 км/ч? Высокий уровень: Г1. (27.Т) В движущемся железнодорожном вагоне есть точки неподвижные и перемещающиеся в сторону, обратную движению вагона в системе отсчёта, связанной с землёй. Какие это точки? Г2. Из города А выехали с одинаковыми скоростями два автомобиля, второй через 12 мин после первого. Они поочередно, с интервалом в 14 мин, обогнали одного и того же велосипедиста. Во сколько раз скорость автомобилей больше скорости велосипедиста? Г3. Расстояние между двумя пристанями моторная лодка проходит по течению за 10 мин, а против течения — за 30 мин. За какое время это расстояние проплывет по течению спасательный круг, упавший в воду? Г4. (22.Т) а) Два катера идут по реке в одну сторону с различными скоростями. В тот момент, когда они поравнялись, с каждого был брошен в воду спасательный круг. Спустя четверть часа катера повернули обратно и с прежними скоростями направились к брошенным в воду кругам. Который из них дойдет до круга раньше: движущийся с большей или меньшей скоростью? б) Ту же задачу решите при условии, когда катера идут первоначально навстречу один другому.
Г6. (5.К) Мимо пристани проплывает плот. В этот момент в поселок, находящийся на расстоянии 15 км от пристани, вниз по реке отправляется катер. Он доплыл до поселка за 45 мин и, повернув обратно, встретил плот на расстоянии 9 км от поселка. Каковы скорость течения реки и скорость катера относительно воды? Г7. (6.К) Два тела движутся навстречу друг другу так, что за каждые 10 с расстояние между ними уменьшается на 16 м. Если эти тела будут двигаться в одном направлении с прежними по величине скоростями, то за 5 с расстояние между ними увеличится на 3 м. С какой скоростью движется каждое из этих тел? Г8. (7.К) Из Харькова в Полтаву с интервалом в 10 минут вышли два электропоезда со скоростями 30 км/ч каждый. С какой скоростью двигался поезд, идущий в Харьков, если электропоезда прошли мимо него с интервалом в 4 минуты? Г9. (8.К) Человек бежит по эскалатору. В первый раз он насчитал 50 ступенек, пробежав весь эскалатор. Во второй раз, двигаясь в ту же сторону со скоростью втрое большей, он насчитал 75 ступенек. Сколько ступенек он насчитал бы на неподвижном эскалаторе? Г10. (9.К) Скорость катера относительно воды 7 м/с, скорость течения реки 3 м/с. Когда катер двигался против течения, с него сбросили в воду мяч. Затем катер прошел против течения 4,2 км, повернул обратно и догнал мяч. Сколько времени двигался катер от момента сбрасывания мяча до встречи с ним? Г11. (35.P) Расстояние s = 240 м необходимо проехать на лодке туда и обратно один раз по реке, скорость течения которой v1 = 1 м/с, а другой раз по озеру. Скорость лодки относительно воды в обоих случаях v2 = 5 м/с. Решив задачу в общем виде, доказать, что поездка туда и обратно по реке всегда занимает больше времени, чем по озеру. На сколько время движения лодки по реке в данном случае больше времени ее движения по озеру? Г12. (10.К) Два поезда идут навстречу друг другу (по параллельным колеям) со скоростями vl и v2. Длина каждого вагона первого поезда, L1, число вагонов n1, второго — соответственно L2 и n2. Сколько времени пассажиры одного поезда видят встречный поезд, не высовываясь из окна? Г13. (11.К) Легковой автомобиль, двигавшийся в 40 м позади автобуса, обгоняет его и опережает на 20 м. Какова скорость встречного грузовика, если в начале обгона расстояние между ним и легковым автомобилем было 800 м, а в конце обгона стало 200 м? Скорость легкового автомобиля при обгоне 90 км/ч, автобуса — 72 км/ч. Г14. (37.Р) Легковой автомобиль движется со скоростью 20 м/с за грузовым, скорость которого 16,5 м/с. В момент начала обгона водитель легкового автомобиля увидел встречный междугородный автобус, движущийся со скоростью 25 м/с. При каком наименьшем расстоянии до автобуса можно начинать обгон, если в начале обгона легковая машина была в 15 м от грузовой, а к концу обгона она должна быть впереди грузовой на 20 м? Г15. (12.К) Спортсмены бегут колонной длиной L со скоростью v. Навстречу бежит тренер со скоростью u < v. Каждый спортсмен, поравнявшись с тренером, разворачивается и начинает бежать назад с той же по модулю скоростью v. Какова будет длина колонны, когда все спортсмены развернутся? Г16. (38.Р) На рис.Г16 приведены графики движения велосипедиста (I) и мотоциклиста (II) в системе отсчета, связанной с землей. Написать уравнение движения велосипедиста в системе отсчета, связанной с мотоциклистом, и построить график его движения в этой системе.
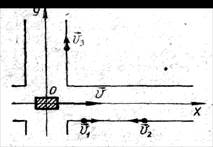
Рис.Г16 Рис.Г17Рис.Г18 Г17. (39.Р) На рис.Г17 изображен график движения второго автомобиля в системе отсчета, связанной с первым автомобилем. Написать уравнения движения и построить графики в системе отсчета, связанной с землей (начало координат расположить в месте нахождения первого автомобиля в начальный момент времени), если скорость первого автомобиля относительно земли: а) направлена по оси X и равна 2 м/с; б) направлена по оси X и равна 6 м/с; в) направлена в сторону, противоположную оси X, и равна 2 м/с. Описать картину движения в каждом случае. Г18. (46.P) В системе отсчета, связанной с землей, трамвай движется со скоростью v = 2,4 м/с (рис.Г18), а три пешехода — с одинаковыми по модулю скоростями v1 = v2 = v3 = 1 м/с. Найти: а) модули скоростей пешеходов в системе отсчета, связанной с трамваем; б) проекции векторов скоростей пешеходов на оси координат в этой системе отсчета.
Г20. (1.15Г) К ползуну, который может перемещаться по направляющей Рис.Г19 рейке (рис.Г20), прикреплен шнур, продетый через кольцо. Шнур выбирают со скоростью v. С какой скоростью и движется ползун в момент, когда шнур составляет с направляющей угол α?
Г22. (1.17Г)Стержень длиной L = 1м
Олимпиадные задачи: Д1. Два тела А к В движутся пересекающимися курсами АС и BD с заданными скоростями v1, и v2. Определите наименьшее расстояние, на которое сближаются эти тела. Задачу решите графически. Д2. (5.35Г) Шарик движется между двумя очень тяжелыми вертикальными параллельными стенками, соударяясь с ними по закону абсолютно упругого удара. Одна из стенок закреплена, другая движется от нее с постоянной горизонтальной скоростью ux = 0,5 м/с. Определить число n соударений и окончательную скорость vx шарика, если перед первым соударением со стенкой она была равна vox = 19,5 м/с.
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 Б5. (28.Р) На рисунке приведена схема полета советских космических станций с посадкой на Венеру. В какой системе отсчета указана траектория полета?
Б5. (28.Р) На рисунке приведена схема полета советских космических станций с посадкой на Венеру. В какой системе отсчета указана траектория полета?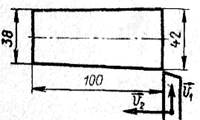 В20. (43.Р) На токарном станке вытачивают деталь в форме усеченного конуса (рис.В20). Какова должна быть скорость поперечной подачи резца, если скорость продольной подачи 25 см/мин? Размеры детали (в миллиметрах) указаны на рисунке.
В20. (43.Р) На токарном станке вытачивают деталь в форме усеченного конуса (рис.В20). Какова должна быть скорость поперечной подачи резца, если скорость продольной подачи 25 см/мин? Размеры детали (в миллиметрах) указаны на рисунке. Г5. (4.К) В некоторой точке А в стороне от шоссе находится человек. На шоссе в точке В человек увидел автобус, движущийся со скоростью va. С какой минимальной скоростью должен бежать человек к шоссе, чтобы успеть на автобус? Задачу решить графически.
Г5. (4.К) В некоторой точке А в стороне от шоссе находится человек. На шоссе в точке В человек увидел автобус, движущийся со скоростью va. С какой минимальной скоростью должен бежать человек к шоссе, чтобы успеть на автобус? Задачу решить графически.

 Г19. (1.14Г) Корабль выходит из пункта А и идет со скоростью v, составляющей угол α с линией АВ (рис.Г19). Под каким углом β к линии АВ следовало бы выпустить из пункта В торпеду, чтобы она поразила корабль? Торпеду нужно выпустить в момент, когда корабль находился в пункте А. Скорость торпеды равна u.
Г19. (1.14Г) Корабль выходит из пункта А и идет со скоростью v, составляющей угол α с линией АВ (рис.Г19). Под каким углом β к линии АВ следовало бы выпустить из пункта В торпеду, чтобы она поразила корабль? Торпеду нужно выпустить в момент, когда корабль находился в пункте А. Скорость торпеды равна u.

 Г21. (1.16Г) Рабочие, поднимающие груз (рис.Г21), тянут канаты с одинаковой скоростью v. Какую скорость и имеет груз в тот момент, когда угол между канатами, к которым он прикреплен, равен 2α?
Г21. (1.16Г) Рабочие, поднимающие груз (рис.Г21), тянут канаты с одинаковой скоростью v. Какую скорость и имеет груз в тот момент, когда угол между канатами, к которым он прикреплен, равен 2α?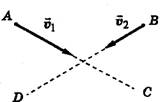 Рис.Г20 Рис.Г21 Рис.Г22 шарнирно соединен с муфтами А и В, которые перемещаются по двум взаимно перпендикулярным рейкам (рис.Г22). Муфта А движется с постоянной скоростью vA = 30 см/с. Найти скорость vB муфты В в момент, когда угол ОАВ = 60°. Приняв за начало отсчета времени момент, когда муфта А находилась в точке О, определить расстояние ОВ и скорость муфты В как функции от времени.
Рис.Г20 Рис.Г21 Рис.Г22 шарнирно соединен с муфтами А и В, которые перемещаются по двум взаимно перпендикулярным рейкам (рис.Г22). Муфта А движется с постоянной скоростью vA = 30 см/с. Найти скорость vB муфты В в момент, когда угол ОАВ = 60°. Приняв за начало отсчета времени момент, когда муфта А находилась в точке О, определить расстояние ОВ и скорость муфты В как функции от времени.


