Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
VI. Нейтральный элемент относительно умножения – единичная матрица (Е)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
AE=A=EA Единичная матрица – квадратная матрица все элементы которой, расположенные на гланой диагонали равны 1, а остальные 0. Eij=1, при i=j VII. Умножение на нулевую матрицу A[mxn] Θ[nxr]= Θ[mxr] 5. VIII. Возведение матрицы в степень (A[mxn])k=AAAAAA…(k раз) 6. Квадратная матрица – матрица у которой i=j. Определитель матрицы – число. Порядок определителя - количество строк или столбцов. Теорема разложения. Определитель матрицы А n-го порядка равен сумме произведений элементов какой-либо строки (столбца) на соответствующие им алгебраические дополнения. 7. D3=a11a22a33 + a12a23a31 + a21a32a13 – a31a22a13 – a32a23a11 – a21a12a33 Вывод правила треугольников. 8. Свойства определителя n-го порядка 1. Если у определителя поменять 2 строки, то определитель изменит знак. 2. Если есть нулевая строка, то определитель равен 0. 3. Если все элементы строки умножить на число, то определитель увеличиться на это число. 4. Определитель 5. det(AB)=detA*debt(без док) 6. 9. Обратные матрицы Матрица А-1 называется обратной для А, если А-1А=АА-1=Е→А – квадратная матрица. Вырожденная матрица – матрица определитель которой равен 0 Теорема: Если А не вырожденная, то существует одна А-1. Доказательство: Пусть А[nxn]= AA-1=E A(1/Δn*Sт)=E (1/Δn)* Доказательство единственности: Предположим, что есть 2 обратных матрицы для А.. A-1 и В А-1А=АА-1=Е BA=AB=E (1-2) А-1А-BA= АА-1-AB=E-E A(A-1-B)=A(A-1-B)=0 A-1-B=0 => (a-1)ij=bij => A-1=B. 10. Матричные уравнения A-1|AX=В→ EX=A-1B→ X=A-1B A – матрица коэффициентов, X – столбец неизвестных. 11. Системы n уравнений X=A-1B= 12. Формула Крамера.
Теорема Крамера. Система из n линейных уравнений м n неизвестными, определитель которой отличен от 0, имеет единственное решение, которое может быть найдено по формуле Крамера. 13. Минор матрицы Ранг матрицы 1. Если в матрице А выделить k строк и k столбцов, то определитель составленный из элементов, стоящих на пересечении этих строк и столбцов называется минором k-го порядка матрицы А. Ранг матрицы – наивысший порядок минора отличный от 0
2. Элементы S1, S2…Sn называются линейно зависимыми, если существует набор чисел n1, n2…nn такой что n1S1+n2S2+…+nnSn=0 и хотя бы одно из чисел ni≠0. Если это выполняется при всех т=0, то элементы называются не линейно зависимыми. Ранг матрицы – количество линейно независимых строк или столбцов этой матрицы. 14. Теорема Кронехера-Копелли Система из m линейных уравнений с n неизвестными совместна тогда и только тогда, когда ранг матрицы А равен рангу расширенной матрицы, причем: 1. если rA=rÂ=n – 1 решение. 2. если rA=rÂ<n - ∞ решений. 3. если rA≠rÂ≤n - нет решений. 16. Совместная система – система, имеющая хотя бы 1 решение. Решение системы – набор чисел такой, что при подстановке в систему каждое уравнение превращает в равенство. Общее решение – решение из которого можно получить все частные решения 1. Все неизвестные выражаются через 1 параметр (кол-во неизвестных = n-rA) 2. Все базисные неизвестные выражаются через свободные члены. Свободное неизвестное – неизвестное в ответе, остальные – базисные Алгоритм Гаусса 1. Найти ai1≠0 и поставить на первое место 2. S1→S1:a11 3. Si→Si-ai1S1, где i=2,3...m 4. Ищем aj2≠0(j≠1) и т.д. если aj2=0 при любом j=2…m, то ищем aj3≠0 (j≠1). 18. Операции над векторами и их свойства 1. Сложение А) Б) В) Г) Противоположные вектора – вектора модули которых равны, но направление противоположное. 19. 2. Умножение вектора на число
Свойства 1. 2. 3. 4. Орт вектора – единичный вектор сонаправленный с данным вектором. 20. Ось – прямая с заданным направлением. Проекция точки – основание перпендикуляра, опущенного из точки на ось. ПрeAB=|AB| или -|AB| Свойства проекции. 1. ПреAB=|AB|cosA Доказательство: 1.A-острый Из треуг. ABB’’: |AB’’| =|AB|cosA
=>|D’C’|=-|DC|cosA 2. ПреAB+ПреВС=Пре(АВ+ВС) Доказательство: 1.А1-угол между AB и e A2 – угол между ВС и е острые ПреАВ=|А’В’| ПреВС=|В’С’ | Пре(АВ+ВС)=|В’С’|+|А’В’| =|A’C’| 2.А1- острый A2 – тупой ПреАВ=|А’В’| ПреВС=-|В’С’ | Пре(АВ+ВС)=|В’С’|-|А’В’| =|A’C’| 3.k*Прea=Преka Доказательство: 1. K>0 => ka||a => угол не меняется Преа=|a|cosA Преka=|ka|cosA=|k|Преа
2. K<0 => угол между ka и e =Pi-A Прeka=|ka|cos(Pi-A)=|k||a|(-cosA)=-|k||a|cosA=kПрea 21. ab=|a||b|cosA Свойства 1. Преа=|a|cosA=ab/|b| Праb=|b|cosA =>ab/|a| => ab=|b|Прba=|a|Праb 2. a(b+c)=ab+ac Доказательство: ab=|a|Прab ac=|a|Прас Пра(b+c)=Праb +Прас =>|a|Pra(b+c)=|a|Prab+|a|Praс => a(b+c)=ab+ac 3. (na)b=a(nb)=n(ab) Доказательство: a(nb)=|a|Prabn=|a|nPrab=n(ab) 4. Два ненулевых вектора а≠0, b≠0 перпендикулярны когда ab=0 и наоборот. Доказательство: 1. если a┴b, то угол A=90o => cosA=0, то ab=0 5. Связь между длиной вектора и скалярным произведением. Aa=|a||a|=|a|2=> |a|= 22. c=axb, если 1. |c|=|a||b|sinA 2. c┴a c┴и 3. a b с образуют первую тройку векторов Свойства 1. геометрический смысл S=axb 2. axb=-bxa 3. ax(b+c)=axb+cxa 4. Умножение вектора на число (na)xb=ax(nb)=n(axb) 23. Смешанное произведение векторов C(axb)=a(bxc)=abc V=abc 24.
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.174.125 (0.011 с.) |

 матрицы равен определителю транспонированной матрицы.
матрицы равен определителю транспонированной матрицы.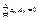 , если i≠j.
, если i≠j.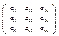 det(a)=0 S=
det(a)=0 S= 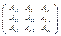 A-1=1/Δn*Sт
A-1=1/Δn*Sт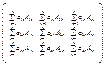 = =(1/Δn)*
= =(1/Δn)* 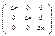 =
= 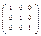
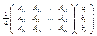 =
= 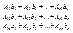
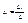 , Δi-определитель полученный из матрицы А если в ней столбец заменить на столбец свободных членов. Вывод
, Δi-определитель полученный из матрицы А если в ней столбец заменить на столбец свободных членов. Вывод



 , если а)
, если а) 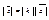
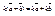

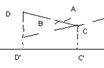 2. A-тупой B=180-A |CC’|=|DC|cosB=|DC|cos(Pi-A)=-|DC|cosA =>
2. A-тупой B=180-A |CC’|=|DC|cosB=|DC|cos(Pi-A)=-|DC|cosA =>