
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Побудова математичних моделей задач управлінняСодержание книги
Поиск на нашем сайте
Серед математичних методів вирішення задач управління найбільш розповсюдженими є методи лінійного програмування. Для цього класу задач характерно: По-перше – показник ефективності (або критерій) лінійно залежить від елементів (або аргументів) рішення; По-друге – обмеження, що накладаються на елементи рішення, мають вид лінійних нерівностей і рівностей. Особливістю цього класу задач є припущення про лінійність, тобто пропорційності залежностей, що розглядаються. Наприклад: сумарна коштовність виготовленої продукції пропорційна її кількості. На практиці лінійні залежності зустрічаються не часто, а значну частину залежностей можливо умовно приймати за лінійні. Задачі лінійного програмування часто використовують при рішенні задач перспективного планування (транспортних задач). Математична модель задачі управління представляється у вигляді цільовій функції, яка відображає основну ціль задачі, що вирішується, і обмежень, які є умовами ситуації, що аналізується.
1. Побудова математичної моделі задачі перспективного планування (оптимального планування)) в процесі управління за критерієм максимізації прибутку Умови: Кожний з підрозділі підприємства виготовляє товар декількох видів. Від реалізації товару підприємство отримує певний прибуток. Необхідно визначити: Скільки груп товару кожного виду підприємство повинно випускати, щоб виходячи з фонду робочого часу, отримати максимальний прибуток. Для більшого розуміння наведено конкретні умови у вигляді прикладу: Основні показники наведено у таблиці 1. Таблиця 1 Показники виробництва
Рішення:
Для побудови математичної моделі задачі необхідно ввести позначення і представити модель у загальному виді: i - підрозділ, j – вид продукції, Xj – обсяг продукції j –го виду, Xij – обсяг продукції j –го виду, що виробляється i-м підрозділом, tij – час необхідний для виробництва j –го виду продукції в i- у підрозділі, Ti – фонд робочого часу підрозділу i- ї групи, Pj – прибуток від реалізації одного виробу j –го виду, Для визначення оптимального плану виробництва продукції за критерієм максимізації прибутку, необхідно скласти математичну модель задачі в загальному вигляді:
Цільова функція: 20Xa + 30Xb →max Обмеження: X1a + 2X1b ≤ 10 X2a + X2b ≤ 6 2X3a + X3b ≤ 10 X1a + X2a + X3a = Xa X1b + X2b + X3b = Xb Xij ≥ 0, 2. Побудова оптимізаційної моделі задачі перспективного планування (транспортна модель) в процесі управління за критерієм мінімізації витрат Умови: З визначеної кількості підприємств до деяких торговельних підприємств поступає товар. Потреба торговельних організацій не більше виробництва підприємств постачальників. Відомо: кількість товару, яке необхідно торговельній організації; кількість товару, що виготовляється підприємствами-постачальниками; собівартість товару і вартість перевезень. Необхідно: спланувати постачання торговельних фірм товаром, щоб витрати були мінімальними. Введемо позначення: j – номер торговельного підприємства, i – номер підприємства-постачальника, Pj – потреба j –го торговельного підприємства в товарі, Ni – потужність i-го підприємства-постачальника, rij – витрати на постачання і придбання товару з i- го підприємства j –го торговельного підприємства, xij – обсяг постачання товару з i- го підприємства на j –е торговельне підприємство, Математична модель задачі в загальному вигляді: Цільова функція: представляє собою суму витрат на постачання товару від кожного підприємства-постачальника кожному торговельному підприємству і це значення повинно бути мінімальним:
Обмеження: по потребі – обсяг товару, що постачається повинен забезпечити задану потребу торговельного підприємства (Pj); по потужності – обсяг кількості товару кожного підприємства-постачальника (Ni) повинен відповідати, тобто дорівнювати або бути більше ніж потреба торговельних підприємств.
У результаті реалізації даної моделі можливо отримати оптимальний план постачання торговельних підприємств сировиною з мінімальними транспортними витратами. Більш детальне розуміння застосування оптимізаційних моделей для вирішення задач перспективного планування в процесі управління буде надано на практичних заняттях.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

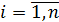 ;
; ;
; ,
,  ;
; ;
;
 (2)
(2)







