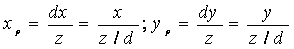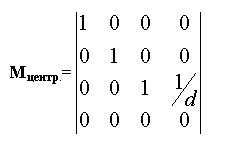Математическое описание плоских проекций

Для простоты будем считать, что при центральном проецировании картинная плоскость перпендикулярна оси Z и совпадает с плоскостью Z = d, а при параллельном проецировании совпадает с плоскостью Z = 0. Проекции рассматриваются в системе координаты наблюдателя. В левосторонней системе ось X направлена вправо, Y – вверх, Z - внутрь экрана, что естественно согласуется с экраном дисплея. Каждую из проекций можно описать матрицей 4х4. Это удобно, поскольку появляется возможность объединить матрицу проецирования с матрицей преобразования.

Рис. 1

Точка P проецируется на проекционную плоскость, расположенную на расстоянии d от начала координат. Для вычисления Xp и Yp - проекции точки (X,Y,Z) -запишем отношения из подобия треугольников

Умножая обе части на d, получаем:

Расстояние d является в данном случае масштабным множителем, примененным к координатам Xp и Yp. Фактором, приводящим к тому, что на центральной проекции более удаленные объекты выглядят мельче, чем ближние, является деление на Z. Отметим, что допустимы все значения Z, кроме Z = 0. Точки могут располагаться, как на оси Z, так и между центром проекции и проекционной плоскостью. Данное преобразование можно представить в виде матрицы 4х4.

Умножая точку P = (X,Y,Z,1) на Мц., получаем общее выражение для точки в однородных координатах:

Теперь, поделив на w (которое равно z /d) для обратного перехода к трем измерениям, имеем:

Результат содержит преобразованную Z-координату d, соответствующую положению проекционной плоскости вдоль оси Z.

Другая схема построения центральной проекции такова:

Эту матрицу можно получить из матрицы Мцентр:

Ортографическое проецирование на плоскость Z = 0 очевидно. Направление совпадает с нормалью к плоскости проекции, в нашем случае с осью Z. Таким образом, точка P имеет координаты Xp= X, Yp= Y, Zp= 0. Эта проекция описывается матрицей

Рассмотрим теперь косоугольную проекцию, матрица которая может быть записана исходя из значений a и l.

Изображен единственный куб, спроецированный на плоскость XOY. Из рисунка видно, что проекцией точки P находящейся на задней стороне куба, является точка P' принадлежащая плоскости XOY. Это означает, что направление проецирования совпадает с отрезком PP', проходящем через эти две точки. Это направление есть P'-P=(lcosa,lsina,-1).

Направление проецирование составляет угол с плоскостью XOY. Теперь рассмотрим произвольную точку (X,Y,Z) и определим ее косоугольную проекцию (Xp,Yp) на плоскость XOY. Показаны два изображения точки и проектор, который параллелен предыдущему. Уравнение для X и Y координат проектора как функций Z имеют вид Y = mZ + b. Решая два уравнения относительно Xp и Yp, получаем:

Матрица 4х4, которая описывает косоугольную проекцию, имеет вид

Применение Мкос приводит к сдвигу и последующему проецированию объекта: плоскости с постоянной координатой Z = Z, переносятся в направлении X на Z*lcosa и в направлении Y на Z*lsina и затем проецируется на плоскость Z = 0. Сдвиг сохраняет параллельность прямых, а также, углы и расстояния в плоскостях, параллельных оси Z.

Для проецирования Кавалье l=1, поэтому угол b, показанный на рисунке равен 45о. Для проецирования Кабине l=1/2, а b=arctg(2)=63.4. В случае ортографической проекции l=0 и b=90, следовательно Морт есть частный случай Мкос.

 

 

Уравнение прямой линии

Явное уравнение прямой линии имеет вид Y=mX+с, где m - тангенс угла наклона; c - точка пересечения с осью Y.

Это явное уравнение для Y позволяет вычислить Y при любом значении Х. Однако у этого уравнения есть один недостаток: с его помощью нельзя описать вертикальные прямые, например X=1. Если прямая проходит через две заданные точки (Х1;Y1) и (Х2;Y2), то явное уравне-ние можно переписать:

или записать (X2 - X1)(Y - Y1)=(Y2 - Y1)(X - X1). Здесь уравнение прямой имеет неявный вид. Это неявная форма задания прямой дает возможность описывать вертикальные пря-мые: если X2=X1, а Y2=/Y1, то мы получаем уравнение вертикальной прямой X=X1.

В общем виде уравнение прямой записывается: aX+bY+c=0.

aX+bY+c=0 - уравнение вертикальной прямой, если b=0.

Уравнения плоских кривых

Уравнение явного вида Y=f(X), где f(X) - заданная функция от X, является удовле-творительным в том случае, когда функция однозначна, а кривая не имеет вертикальных касательных.

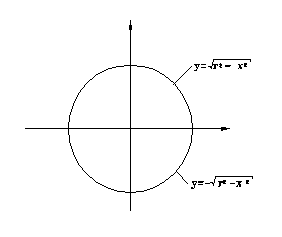
Неявное уравнение X*X+Y*Y-r*r=0 применяется для окружности. Неявное уравнение в общем случае записывается в виде f(X,Y)=0, где f(X,Y) - функция от X и Y.

Наиболее распространенными неявными уравнениями являются уравнения кониче-ских сечений.

Уравнение для эллипса

Уравнение для параболы Y*Y-4aX=0.

Уравнение для гиперболы

В общий случае, все типы конических сечений описываются уравнением второй сте-пени: S=aX*X+2hXY+bY*Y+2gX+2fY+c=0, где a,b,c,f,g,h – различные между собой коэффициенты.

Если выполняется соотношение h*h<2, то кривая принимает вид эллипса; если h*h=ab, то вид параболы; если h*h>ab, то гиперболы, при условии, что abc+2fgh-2fgh-af*f-bg*g-ch=/0