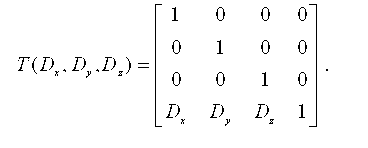Методы моделирования логических устройств

Интерактивный диалог в графических программах требует наличия логических устройств ввода - локатора, селектора, валуатора, клавиатуры и кнопок. Однако логическую функцию любого из этих устройств можно реализовать с помощью физического устройства из любого другого класса, хотя не всегда удачно. С другой стороны, не всегда целесообразно, чтобы для каждого логического устройства имелись отдельные физические устройства. Многие распространенные интерактивные графические системы имеют позиционирующие устройства (планшет, мышь) и клавиатуру с функциональными кнопками. С помощью этих трех физических устройств реализуются все логические функции. Ниже представлены логические устройства ввода и возможные физические устройства для их (логических устройств) моделирования.

Моделирование локатора

Световое перо; Управление курсором с клавиатуры; Управление курсором параметрически с клавиатуры. Ввод координат; Управление курсором мышью

Моделирование селектора

Выбор курсором объекта; Ввод с клавиатуры имени объекта.

Моделирование валуатора

Ввод значения на клавиатуре; Работа со шкалой.

Моделирование клавиатуры

Распознавание литер. Распознавание рукописных текстов; Изображение клавиатуры на дисплее.

Моделирование кнопок

Меню иерархическое, которое делится на статическое и динамическое; Световые кнопки.

 

Матричное представление 3D преобразований

По аналогии с 2D преобразованиями, которые описываются матрицами 3x3, 3D преобразования могут быть представлены в виде матриц 4x4. И тогда трехмерная точка (X, Y, Z) записывается в однородных координатах как (W*X, W*Y, W*Z, W), где W=/0. Если W=/1 для получения декартовых координат точки (X, Y, Z) первые три ко-ординаты делятся на W. Две точки H1 и H2 в пространстве однородных координат описывают одну и ту же точку 3D пространства только в том случае, если H1=cH2 для любой константы с=/0 Система координат правосторонняя. Перевод каждой положительной полуоси в другую, осуществляется против часовой стрелки.

В машинной графике, часто удобнее использоваться левосторонней системой ко-ординат. Это позволяет легко интерпретировать тот шаг, что точки с большим Z нахо-дятся дальше от наблюдателя.

Отметим, что в левосторонней системе координат положительными поворотами будут повороты, выполняемые по часовой стрелке.

Трехмерный перенос

Трехмерный перенос является простым расширением двумерного:

Масштабирование

Поворот

Двумерный поворот, описанный ранее, является в тоже время трехмерным пово-ротом вокруг оси Z. В 3D поворот относительно Z описывается следующим образом:

Это легко проверить: в результате поворота на 90гр. вектора [1 0 0 1], являющегося единичным вектором оси X, должен получиться единичный вектор оси Y [0 1 0 1]. Вычисляя произведение

получаем предсказанный результат. Матрица поворота вокруг оси X имеет вид

 

Матрица поворота вокруг оси Y записывается в виде

 

Композиция 3D преобразований

Объединением элементарных 3D преобразований можно получить сложные пре-образования, выполняемые над объектами в моделируемой сцене. Пример сложного преобразования рассмотрим на практической задаче.

Задача:

Преобразовать отрезки [P1P2] и [P1P3] из начальной позиции в конечную. P1 в начало координат, P1P2 вдоль оси Z, P1P3 в плоскости YOZ, где ось Y положительна. На длины отрезков преобразования не влияют.

Этапы решения:

1. Перенос точки P1 в начало координат.

2. Поворот вокруг оси Y до совмещения P1P2 c плоскостью YOZ.

3. Поворот вокруг оси X до совмещения P1P2 c отрицательным Z.

4. Поворот вокруг оси Z до совмещения P1P3 c плоскостью YOZ.

Шаг 1.

Перенос P1 в 0

Применение переноса к P1, P2, P3 дает следующие результаты:

Шаг 2.

Поворот вокруг оcи Y. Поворот на положительный угол 0 для которого:

 

Подставим эти выражения в матрицу Ry(0), тогда

 

Как и ожидалось x-компонента P2''=0.

Шаг 3.

Поворот вокруг оси X. Рисунок после второго шага.

Шаг 4.

Рисунок после шага 3.