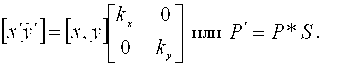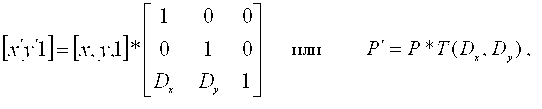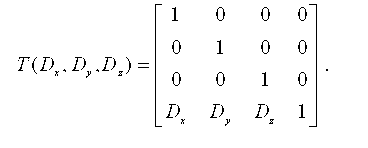Машинная графика. Интерактивная графика. Применение. Классификация. Перспективы применения.

Машинная графика. Интерактивная графика. Применение. Классификация. Перспективы применения.

САПР - это человеко-машинная система, позволяющая на базе ЭВМ автоматизировать определенные функции, выполняемые человеком, с целью повышения темпов и качества проектирования, представляющая собой вид информационного процесса, лежащего в основе технической подготовки производства.

Машинная графика - это создание, хранение и обработка моделей объектов и их изображений с помощью ЭВМ. Машинная графика в автоматизированном проектировании позволяет: освободить человека от выполнения однообразных, трудоемких графических операций, которые можно формализовать и тем самым повысить производительность труда в проектировании, так как трудозатраты на выполнение, например, рабочих чертежей объектов машиностроения составляют значительную часть общего объема проектных работ; благодаря возможности быстрого перебора многих вариантов, решать одну из основных задач проектирования - поиск оптимального варианта; обеспечивать естественную связь человека с ЭВМ на уровне основной продукции инженера любой специальности - графической. Машинная графика, как подсистема САПР, включает в себя методическое, лингвистическое, математическое, программное, техническое, информационное и организационное обеспечение. Методическое обеспечение - документы, в которых отражены состав, правила отбора и эксплуатации средств автоматизации проектирования. Лингвистическое обеспечение - языки проектирования, терминология, правила формализации естественного языка. Математическое обеспечение - основано на методе математического моделирования, согласно которому математическая структура, отношения элементов в математической модели соответствуют структуре и отношениям в реальном объекте. В МГ используется геометрическая версия математического моделирования, при котором двумерные и трехмерные изображения состоят из точек, линий и поверхностей. Программное обеспечение - включает программы на машинных носителях, тексты программ и эксплутационную документацию. Основу программного обеспечения МГ составляют пакеты прикладных программ (ППП), представляющие собой набор программ, реализующих на ЭВМ инвариантные и объектно-ориентированные графические процедуры. Техническое обеспечение - устройства вычислительной и организационной техники, средства передачи данных, измерительные и другие устройства или их сочетания. Информационное обеспечение - документы, содержащие описание стандартных проектных процедур, типовых проектных решений, типовых элементов, комплектующих изделий, материалов и другие данные, а также файлы и блоки данных на машинных носителях с записью указанных документов. Организационное обеспечение - положения, инструкции, приказы, квалификационные требования и другие документы, регламентирующие организационную структуру подразделений и взаимодействие их с комплексом средств автоматизации проектирования.

Применение машинной графики

В применении машинной графики различают два уровня: пассивная графика, когда с помощью пакета прикладных программ производятся формирование и вывод графических изображений; интерактивная графика - процесс оперативного графического взаимодействия (диалога) человека с ЭВМ. Интерактивная машинная графика представляет собой важный раздел МГ, когда пользователь имеет возможность динамически управлять содержанием изображения, его формой, размерами и цветом на поверхности дисплея с помощью интерактивных устройств взаимодействия, например клавиатуры, мыши, трекбола и т.п. Интерактивная машинная графика существенно повышает эффективность диалога пользователя с ЭВМ за счет использования сочетания графического информации с текстовой. В итоге повышается качество и точность результатов, снижаются объемы рутинной работы. Типичными примерами использования интерактивной графики являются следующие области:

создание графиков, гистограмм, диаграмм; геоинформационные системы, картография; автоматизация чертежных и конструкторских работ; САПР; проектирование компонент и систем механических, электрических, электромеханических и электронных устройств; проектирование и моделирование в авиа-, судо-, автомобилестроении; архитектура, дизайн, геология; моделирование спецэффектов, мультипликация, заставки; управление процессами; автоматизация канцелярских работ, электронный документооборот, электронная публикация; искусство и реклама; графические интерфейсы операционных и прикладных систем, броузеров для Интернета и WEB-серверов; компьютерные игры, библиотеки и энциклопедии на СD-ROM, интерактивное кино.

1. Тип объекта:

а) линейные рисунки двумерных объектов; б) каркасное представление трехмерных (3D) объектов; в) каркасное представление 3D объектов с удалением невидимых линий. г) поверхностное представление 2D объектов. Двумерные тоновые изображения - черно-белые и цветные; д) трехмерное поверхностное представление 3D объектов с удалением невидимых линий и поверхностей; е) трехмерное поверхностное представление 3D объектов с удалением невидимых линий и поверхностей и отображением фактур поверхностей; ж) твердотельное представление объектов.

2.Тип выводимого изображения:

а) ортогональные проекции; б) аксонометрия (косоугольная, прямоугольная); в) перспектива, наглядные изображения.

3. Тип интерактивности и уровень возможностей для управления диалогом и изображением:

а) автономное вычерчивание по готовой базе данных с помощью прикладной программы на графопостроителе; б) интерактивный диалог по созданию чертежей по готовой базе данных; в) интерактивный графический диалог по созданию чертежей и интерактивное графическое пространственное проектирование. 4. Роль изображения: а) цель. Инструментальное средство. Архитектура, дизайн, картография, реклама, искусство; б) компонента. Подсистема САПР.

В свою очередь, использование и распространение машинной графики становится оправданным для широкого круга приложений вследствие быстрых темпов удешевления аппаратно-технических средств.

 

Преобразование на плоскости называется аффинным, если оно взаимно однозначным образом преобразует точку в точку, прямую в прямую и кривую линию в кривую. Аффинное преобразование на плоскости (от англ. affinity – родство) имеет следующие свойства:

· отображает двумерный объект в двумерный (точку в точку, прямую в прямую и кривую линию в кривую линию);

· Сохраняет параллельность линий;

· Сохраняет пропорции параллельных объектов, длин параллельных отрезков и площадей плоских фигур.

Множество аффинных преобразований на плоскости (АП) может быть представлено на основе элементарных АП таких как, Перенос, Поворот, Масштабирование, Симметрия относительно точки, Симметрия относительно оси (Зеркальное отображение). Эти преобразования будем называть базовыми преобразованиями (БП), в силу того, что на их основе можно описывать сложные композиции АП. Т.е. сложное АП можно представить как комбинацию последовательных БП через их произведение с получением матричной записи данного сложного результирующего преобразования.

1. Перенос (англ. Transfer). Точки на плоскости, в неподвижной системе координат XOY, можно перенести в новые позиции на величину вектора переноса Т с компонентами переноса (Dx, Dy), путем добавления к координатам этих точек значений компонент вектора переноса. Для каждой точки плоскости P(x,y), которая переносится на вектор Т с компонентами переноса Dx (параллельно оси OX)и Dy (параллельно оси OY), можно записать следующие координатные уравнения для определения значений координат новой точки P’(x’y’):

x'= x + Dx,

y' = y’ + Dy

или, в матричном виде [ x’ y’ ] = [ x y ] + [ Dx Dy ]. Перенос обозначается как T ( Dx Dy ).

2. Поворот (англ. Rotation). Поворот точки на плоскости, в неподвижной системе координат XOY, относительно центра системы координат на заданный угол a описывается следующими координатными уравнениями:

x'= x *Cos a - y * Sin a

y' = x *Sin a + y * Cos a

или, в матричном виде [ x’ y’ ] = [ x y ] * [ Cos a Sin a ]

[ - Sin a Cos a ].

Необходимо различать Поворот в положительном направлении на угол a (против часовой стрелки) и в отрицательном направлении на угол - a (по часовой стрелке). Поворот обозначается как R ( a ).. Тогда R (- a )= R^Т ( a ).

3. Масштабирование (англ. Scaling). Масштабирование на плоскости по своей сути является растяжением-сжатием вдоль осей координат. Объекты на плоскости, в неподвижной системой координат XOY, можно растянуть в K _x раз вдоль оси OX и в K_y раз вдоль оси OY, получив в результате новые точки объекта, где K _x и K_y - коэффициенты масштабирования вдоль соответствующих осей. Если K _x = K_y, то масштабирование называется однородным. Если K _x ≠ K_y, то масштабирование называется неоднородным. Масштабирование описывается следующими координатными уравнениями:

x'= x * K _x

y' = y * K_y

или, в матричном виде [ x’ y’ ] = [ x y ] * [ K _x 0 ]

[ 0 K_y ].

Масштабирование обозначается как S ( K _x K_y ).

4. Симметрия относительно точки. Преобразование симметрии на плоскости в неподвижной системе координат XOY относительно центра системы координат есть, по своей сути, известное БП Поворот на угол p. В матричном виде базовое преобразование симметрии можно записать:

[ x’ y’ ] = [ x y ] * [ -1 0 ]

[ 0 -1 ].

Симметрию относительно точки будем обозначать как Sm.

5. Симметрия относительно оси, проходящей через начало координат. Преобразование симметрии на плоскости, в неподвижной системе координат XOY, относительно оси, проходящей через центр системы координат (задаваемой уравнением прямой вида y = f (x)), определяется следующими координатными уравнениями:

x'= x *Cos j + y * Sin j

y' = x *Sin j - y * Cos j,

где угол j =2a. А угол a есть угол наклона прямой к оси ОХ.

Или, в матричном виде [ x’ y’ ] = [ x y ] * [ Cos j Sin j ]

[ Sin j - Cos j ].

Симметрию относительно оси, проходящей через начало координат, будем обозначать как Sm ( j ).

Запишем БП в сжатом виде. Тогда Перенос, Поворот, Масштабирование и Симметрия относительно оси будут определяться в следующем виде, соответственно:

P’ = P + T (Dx Dy)

P’ = P * R (a)

P’ = P * S (K_x K_y)

P’ = P * Sm (j).

Можно отметить, что Перенос, к сожалению, реализуется сложением, а Поворот, Масштабирование и Симметрия умножением. Так как сложное АП необходимо определять, как комбинацию последовательных БП, через их произведение, то желательно, представлять все преобразования на основании одного действия «умножения», чтобы их можно было легко объединять. Т.е. необходимо избавиться от действия «сложения» при определении значений координат в результате Переноса. Для этого, целесообразно, осуществить переход от Декартовых координат к треугольным координатам на плоскости, которые будем называть однородными. Однородные координаты широко применяются в проективной геометрии и предоставляют возможность задание точки на плоскости в треугольной системе координат, как расстояние от точки до каждой прямой. Известная Декартова система координат, есть частный случай треугольной системы координат, когда одна из прямых находится в бесконечности.

В этом случае, Декартова координата точки P(x y) записывается как P (X, Y, w ) в однородной системе координат (треугольной), для любого масштабного множите w ¹ 0. При этом, если для точки задано представление в однородных координатах P (X, Y, w ), то можно найти ее двумерные декартовы координаты как x=X/ w и y=Y/ w. Если принять w =1, то деление на единицу делает переход от декартовых координат к однородным и обратно тривиальным.

Будем рассматривать случай, когда w =1. Точки теперь описываются тремя элементарными вектор-строками. Поэтому матрицы преобразований должны иметь размерность 3 х 3. Если выразить точки в однородных координатах, то все три преобразования можно реализовать с помощью умножения, в том числе и Перенос. И это есть главный результат перехода к однородным координатам.

Тогда, уравнение Переноса будет иметь вид:

[ x’ y’ 1 ] = [ x y 1 ] * [ 1 0 0 ]

[ 0 1 0 ]

[ Dx Dy 1 ].

Уравнение Поворота будет иметь вид:

[ x’ y’ 1 ] = [ x y 1 ] * [ Cos a Sin a 0 ]

[ - Sin a Cos a 0 ]

[ 0 0 1 ].

Уравнение Масштабирования будет иметь вид:

[ x’ y’ 1 ] = [ x y 1 ] * [ K _x 0 0 ]

[ 0 K_y 0 ]

[ 0 0 1 ].

Уравнение Симметрии относительно точки :

[ x’ y’ 1 ] = [ x y 1 ] * [ -1 0 0 ]

[ 0 -1 0 ]

[ 0 0 1 ].

И уравнение Симметрии относительно оси :

[ x’ y’ 1 ] = [ x y 1 ] * [ Cos j Sin j 0 ]

[ Sin j - Cos j 0 ]

[ 0 0 1 ],

где угол j =2a и угол a есть угол наклона прямой (оси симметрии) к оси ОХ.

Композиция преобразований:

1) Вращения вокруг произвольного центра

Осуществляется поворот вокруг точки с координатами x = m, y = n на угол a против часовой стрелки. Преобразования выполняется как последовательность трех преобразований:

1. Сдвиг центра вращения в начало координат.

2. Поворот на угол a вокруг начала координат.

3. Сдвиг центра вращения в исходное положение.

Матрицы аффинных преобразований не зависят от преобразуемых точек. Результирующее преобразование записывается в виде:

[ Cosa Sina 0 ] [ - Sina Cos a 0 ] [ 0 0 1 ].

[ 1 0 0 ] [ 0 1 0 ] [ -m -n 1 ]

[ x’ y’ 1 ] = [ x y 1 ] * * *

 

[ 1 0 0 ] [ 0 1 0 ] [ m n 1 ]

[ Cosa Sina 0 ] [ - Sina Cos a 0 ] [ -m(Cosa -1)+n*Sina -mSina -n*(Cosa -1) 1 ]

* = [ x y 1 ] *

 

 

Последняя матрица определяет результирующее преобразование – композицию преобразований - как результат перемножения трех матриц БП.

2) Симметрия относительно оси, не проходящей через начало координат

Пусть ось симметрии наклонена к оси ОX под углом a и пересекает ось в точке х = m. Тогда результирующее преобразование определяется как последовательность базовых преобразований:

1. Сдвиг оси симметрии параллельно себе в начало координат.

2. Симметрия относительно оси проходящей через начало координат.

3. Возврат оси в исходное положение.

Результирующее преобразование принимает вид, угол j =2a:

[ 1 0 0 ] [ Cos a Sin a 0 ]

[ x’ y’ 1 ] = [ x y 1 ] * [ 0 1 0 ] * [ - Sin a Cos a 0 ] *

[ -m -n 1 ] [ 0 0 1 ]

[ 1 0 0 ] [ 0 1 0 ] [ m 0 1 ]

[ Cos j Sin j 0 ] [ Sin j -Cos j 0 ] [ m*(1- Cos j) -m* Sin j 1 ]

* = [ x y 1 ] *

Последняя матрица определяет результирующее преобразование симметрий относительно оси, не проходящей через начало координат – композицию преобразований - как результат перемножения трех матриц БП.

 

Преобразования на плоскости

Точки на плоскости XOY можно перенести в новые позиции путем добавления к координатам этих точек констант переноса. Для каждой точки P(X,Y), которая перемещается параллельно оси X на Dx и параллельно Y на Dy, можно записать уравнения

X'= X + Dx; Y'= Y + Dy, Dx=4, Dy=5.

Вышеприведенные положения точек можно записать через вектор строки: P=[X; Y] P'=[X'; Y'] T=[Dx; Dy]. Уравнение можно переписать в векторной форме: [X', Y']=[X, Y]+[Dx, Dy], или кратко P'=P+T, где Т- матрица переноса.

Поворот

где R- матрица поворота.

Положительными считаются углы, измеренные против часовой стрелки. В случае отрицательных углов можно воспользоваться тождеством для модификации уравнений:

Уравнения (*) легко получаются из примера:

Масштабирование

Объекты можно промасштабировать, т.е. растянуть в к раз вдоль оси X и к вдоль оси Y, получив в результате новые точки, где Kx, Ky - коэффициенты масштабирования вдоль осей.

Различают однородные (Kx = Ky), и неоднородные: (Kx =/ Ky) масштабирования. Преобразование

определяет матрицу масштабирования

Запишем

Однородные координаты и композиция матричных преобразований

В матричном виде преобразования записываются таким образом:

Можно отметить, что перенос, к сожалению, реализуется сложением, а поворот и масштабирование с помощью умножения. Желательно представлять все три преобразования таким образом, чтобы их можно было легко объединять.

Если мы выразим точки в однородных координатах, то все три преобразования можно реализовать с помощью умножения.

В однородных координатах точка P(X,Y) записывается как P(w*X,w*Y,w), для любого масштабного множителя w=/ 0, при этом, если для точки задано представление в однородных координатах P(X,Y,w), то можно найти ее двумерные декартовы координаты как X=X/w; Y=Y/w

Мы будем рассматривать случай, когда w =1, поэтому операции деления не требуется. Точки теперь описываются тремя элементарными вектор-строками. Поэтому матрицы преобразований, на которые умножаются вектор точки, должны иметь размерность3х3.

Уравнение переноса будет иметь вид:

где

Перенос аддитивен:

Уравнение масштабирования в матричной форме записывается:

Масштабирование мультипликативно:

Уравнение поворота:

Поворот аддитивен.

 

Устройства ввода

В рамках рассматриваемой предметной области следует ввести понятие, которое определяет инвариантный набор устройств взаимодействия с любой подсистемой проектирования - логические интерактивные устройства. К ним относятся:

1. Логические устройства ввода: кнопка (устройство для задания выбора); селектор (устройство для указания информации выведенной на экран); клавиатура (устройство для ввода цепочек литер); валуатор (устройство для генерации величин с плавающей точкой); локатор (устройство для задания экранных координат).

Каждое из этих логических устройств отвечает за определенный вид взаимодействия и ввода информации. Следует отметить, что каждому логическому устройству ввода можно поставить в соответствие физическое устройство ввода.

2. Физические устройства ввода: клавиатура; световое перо; мышь, трекболл, трекпоинт, джойстик; планшет, диджитайзер; шар, рычаг; двухмерный или трехмерный звуковой планшет; сканер.

При этом следует отметить, что для реализации полноценного взаимодействия с подсистемами проектирования нет необходимости в наборе всех физических устройств ввода.

Трехмерный перенос

Трехмерный перенос является простым расширением двумерного:

Масштабирование

Поворот

Двумерный поворот, описанный ранее, является в тоже время трехмерным пово-ротом вокруг оси Z. В 3D поворот относительно Z описывается следующим образом:

Это легко проверить: в результате поворота на 90гр. вектора [1 0 0 1], являющегося единичным вектором оси X, должен получиться единичный вектор оси Y [0 1 0 1]. Вычисляя произведение

получаем предсказанный результат. Матрица поворота вокруг оси X имеет вид

 

Матрица поворота вокруг оси Y записывается в виде

 

Композиция 3D преобразований

Объединением элементарных 3D преобразований можно получить сложные пре-образования, выполняемые над объектами в моделируемой сцене. Пример сложного преобразования рассмотрим на практической задаче.

Задача:

Преобразовать отрезки [P1P2] и [P1P3] из начальной позиции в конечную. P1 в начало координат, P1P2 вдоль оси Z, P1P3 в плоскости YOZ, где ось Y положительна. На длины отрезков преобразования не влияют.

Этапы решения:

1. Перенос точки P1 в начало координат.

2. Поворот вокруг оси Y до совмещения P1P2 c плоскостью YOZ.

3. Поворот вокруг оси X до совмещения P1P2 c отрицательным Z.

4. Поворот вокруг оси Z до совмещения P1P3 c плоскостью YOZ.

Шаг 1.

Перенос P1 в 0

Применение переноса к P1, P2, P3 дает следующие результаты:

Шаг 2.

Поворот вокруг оcи Y. Поворот на положительный угол 0 для которого:

 

Подставим эти выражения в матрицу Ry(0), тогда

 

Как и ожидалось x-компонента P2''=0.

Шаг 3.

Поворот вокруг оси X. Рисунок после второго шага.

Шаг 4.

Рисунок после шага 3.

 

Векторная алгебра

Векторы - объекты, имеющие величину и направление. Векторы обозначаются a, b, OP и т.д. Вектор можно изобразить в виде направленного отрезка, длина которого в некотором масштабе соответствует величине вектора, а направление этого отрезка совпадает с на-правлением вектора a. Ориентацию вектора вдоль прямой указывает стрелка.

Вектор, величина которого равна нулю, называется нулевым вектором и обозначается через 0. Нулевой вектор не имеет направления. Векторами являются объекты, которые подчиняются законам векторной алгебры:

1. Равенство. Два вектора считаются равными, если они имеют одинаковую ве-личину, направление и ориентацию: a=b.

2. Сложение. Пусть даны 2 вектора a и b. Найти сумму a+b.

3. Противоположный вектор. (- a) - это вектор величина и ориентация, которого такие же, как и у вектора a, но направление противоположно.

4. Вычитание. По определению a-b=a+(-b).

 

5. Умножение на скаляр. Вектором La, L > 0 является вектор ориентация и направление которого, те же, что и у вектора a, но величина в L раз больше a. Параметр L - обычное число или скаляр.

Уравнение прямой линии

Явное уравнение прямой линии имеет вид Y=mX+с, где m - тангенс угла наклона; c - точка пересечения с осью Y.

Это явное уравнение для Y позволяет вычислить Y при любом значении Х. Однако у этого уравнения есть один недостаток: с его помощью нельзя описать вертикальные прямые, например X=1. Если прямая проходит через две заданные точки (Х1;Y1) и (Х2;Y2), то явное уравне-ние можно переписать:

или записать (X2 - X1)(Y - Y1)=(Y2 - Y1)(X - X1). Здесь уравнение прямой имеет неявный вид. Это неявная форма задания прямой дает возможность описывать вертикальные пря-мые: если X2=X1, а Y2=/Y1, то мы получаем уравнение вертикальной прямой X=X1.

В общем виде уравнение прямой записывается: aX+bY+c=0.

aX+bY+c=0 - уравнение вертикальной прямой, если b=0.

Уравнения плоских кривых

Уравнение явного вида Y=f(X), где f(X) - заданная функция от X, является удовле-творительным в том случае, когда функция однозначна, а кривая не имеет вертикальных касательных.

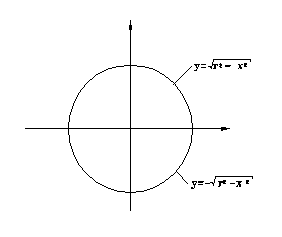
Неявное уравнение X*X+Y*Y-r*r=0 применяется для окружности. Неявное уравнение в общем случае записывается в виде f(X,Y)=0, где f(X,Y) - функция от X и Y.

Наиболее распространенными неявными уравнениями являются уравнения кониче-ских сечений.

Уравнение для эллипса

Уравнение для параболы Y*Y-4aX=0.

Уравнение для гиперболы

В общий случае, все типы конических сечений описываются уравнением второй сте-пени: S=aX*X+2hXY+bY*Y+2gX+2fY+c=0, где a,b,c,f,g,h – различные между собой коэффициенты.

Если выполняется соотношение h*h<2, то кривая принимает вид эллипса; если h*h=ab, то вид параболы; если h*h>ab, то гиперболы, при условии, что abc+2fgh-2fgh-af*f-bg*g-ch=/0

 

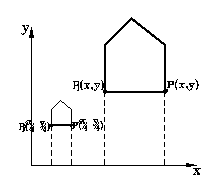
Проекции

В общем случае проекции преобразуют точки, заданные в системе координат размерностью n, в точки системы координат меньше чем n. С помощью проецирования три измерения отображаются в два. Проекции трехмерного объекта (представленного в виде совокупности точек) строится при помощи прямых проецирующих лучей, которые называются проекторами и которые выходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию.

На рисунках показаны две различные проекции отрезков, а также проекторы, проходящие через его конечные точки. Проекция отрезка является отрезком, поэтому достаточно спроецировать лишь одни конечные точки. Определенный таким образом класс проекций известен под названием плоских геометрических проекций, поскольку проецирование в этом случае производится на плоскость, а не на кривую поверхность, и в качестве проекторов используются прямые, а не кривые линии. Плоские геометрические поверхности, которые в дальнейшем будем называть просто проекциями, можно подразделить на два основных класса: центральные и параллельные. Различие между ними определяется соотношением между центром проекции и проекционной плоскостью. Если расстояние между ними конечно, то проекция будет центральной, если же оно бесконечно, то проекция будет параллельной. Параллельные проекции названы так потому, что центр проекции бесконечно удален и все проекторы параллельны. При описании центральной проекции мы явно задаем центр проекции, в то время как определяя параллельную проекцию, мы указываем направление проецирования. Центральная проекция порождает визуальный эффект, аналогичный тому, к которому приводят фотографические системы или зрительная система человека, и поэтому используются в случаях, в которых желательно достичь определенной степени реальности. Этот эффект известен как перспективное укорачивание. Размер центральной проекции объекта изменяется пропорционально расстоянию от центра проекции до объекта. Это означает, что хотя центральная проекция и является реалистичной, она оказывается непригодной для представления точной формы и размеров объектов; из проекции нельзя получить информацию о расстояниях, углы сохраняются только на тех гранях объекта, которые параллельны проекционной плоскости; проекции параллельных линий в общем случае не параллельны. Параллельная проекция порождает менее реалистичное изображение, поскольку отсутствует перспективное укорачивание, хотя при этом могут иметь различные постоянные укорачивания вдоль каждой из осей. Проекция фиксирует истинные размеры, и параллельные прямые остаются параллельными. Как и в случае центральной проекции, углы сохраняются только на тех гранях объекта, которые параллельны проекционной плоскости.

Центральные проекции

Центральные проекции любой совокупности параллельных прямых, которые не параллельны проекционной плоскости, будут сходиться в точке схода. Параллельные прямые в 3D пространстве пересекаются лишь в бесконечности, поэтому точку схода можно представить себе как проекцию точки, находящейся в бесконечности. Если совокупность прямых параллельна одной из главных координатных осей, то их точка схода называется главной точкой схода. Существует только три такие точки (по количеству координатных осей). Если проекционная плоскость пересекает одну ось z, следовательно, перпендикулярна ей, то лишь на этой оси будут лежать главные точки схода, поскольку прямые параллельные осям x и y, параллельны проекционной плоскости и не имеют точек схода. Центральные проекции классифицируются в зависимости от числа главных точек схода,которыми они обладают, а следовательно, от числа координатных осей, которые пересекает координатная проекционная плоскость. Двухточечная центральная проекция широко применяется в архитектурном, инженерном и промышленном проектировании, в рекламных изображениях. Трехточечные центральные проекции почти не используются потому что их трудно конструировать и они мало повышают реалистичность.

Параллельные проекции

Параллельные проекции разделяются на два типа, в зависимости от соотношения между направлениями проецирования и нормалью к проецированной плоскости. В ортографических параллельных проекциях эти два направления совпадают. В косоугольных параллельных проекциях они не совпадают. Наиболее широко используемыми видами ортографических проекций являются: вид спереди, вид слева, вид справа, вид сверху, в которых картинная плоскость перпендикулярна главным координатным осям, совпадающими с направлением проецирования. Косоугольные проекции сочетают в себе свойства ортографических проекций и аксонометрических. В этом случае проекционная плоскость перпендикулярна одной оси, а направление проецирования не перпендикулярно картинной плоскости.

 

 

Кривизна

Радиус кривизны R кривой Y=Y(X) определяется известной формулой

Так как R бесконечен в точках перегиба кривой, удобнее пользоваться самой кривизной H=1/R, поскольку это величина конечная, если нет заострений на кривой:

Соответствующая формула в параметрическом виде кривой X=X(t), Y=Y(t).

В неявном виде f(X;Y)=0

Вывод последних двух формул рекомендуется выполнить самостоятельно.

 

Машинная графика. Интерактивная графика. Применение. Классификация. Перспективы применения.

САПР - это человеко-машинная система, позволяющая на базе ЭВМ автоматизировать определенные функции, выполняемые человеком, с целью повышения темпов и качества проектирования, представляющая собой вид информационного процесса, лежащего в основе технической подготовки производства.

Машинная графика - это создание, хранение и обработка моделей объектов и их изображений с помощью ЭВМ. Машинная графика в автоматизированном проектировании позволяет: освободить человека от выполнения однообразных, трудоемких графических операций, которые можно формализовать и тем самым повысить производительность труда в проектировании, так как трудозатраты на выполнение, например, рабочих чертежей объектов машиностроения составляют значительную часть общего объема проектных работ; благодаря возможности быстрого перебора многих вариантов, решать одну из основных задач проектирования - поиск оптимального варианта; обеспечивать естественную связь человека с ЭВМ на уровне основной продукции инженера любой специальности - графической. Машинная графика, как подсистема САПР, включает в себя методическое, лингвистическое, математическое, программное, техническое, информационное и организационное обеспечение. Методическое обеспечение - документы, в которых отражены состав, правила отбора и эксплуатации средств автоматизации проектирования. Лингвистическое обеспечение - языки проектирования, терминология, правила формализации естественного языка. Математическое обеспечение - основано на методе математического моделирования, согласно которому математическая структура, отношения элементов в математической модели соответствуют структуре и отношениям в реальном объекте. В МГ используется геометрическая версия математического моделирования, при котором двумерные и трехмерные изображения состоят из точек, линий и поверхностей. Программное обеспечение - включает программы на машинных носителях, тексты программ и эксплутационную документацию. Основу программного обеспечения МГ составляют пакеты прикладных программ (ППП), представляющие собой набор программ, реализующих на ЭВМ инвариантные и объектно-о