Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні термодинамічні процесиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ІДЕАЛЬНОГО ГАЗУ 6.1. Загальні питання дослідження процесів
До основних термодинамічних процесів, що мають велике значення для аналізу роботи технічних систем, відносяться такі: ізохорний – це процес, що відбувається при незмінному об’ємі ізобарний – це процес, що відбувається при незмінному тиску ізотермічний – це процес, що відбувається при незмінній температурі адіабатний – це процес, що відбувається без теплообміну з навколишнім середовищем. Крім того існує величезна група процесів, які характеризуються незмінною теплоємністю процесу та називаються політропними. До цієї групи відносяться також і названі основні процеси. Дослідження всіх процесів будемо проводити за однією методикою, яка полягає в наступному: – встановлюється рівняння, що пов’язує між собою основні термодинамічні параметри на початку та в кінці процесу і виводиться рівняння кривої процесу для – визначається зміна внутрішньої енергії, ентальпії та ентропії в процесі; – визначаються робота розширення газу в процесі та тепло процесу; – будуються графіки процесів у
Ізохорний процес Ізохорним називається процес, що відбувається при незмінному об’ємі. Зв’язок між основними термодинамічними параметрами газу в цьому процесі встановлюється безпосередньо з рівняння стану ідеального газу:
звідси при
Отже
тобто, в ізохорному процесі тиск газу змінюється пропорційно температурі. Зміну внутрішньої енергії газу в процесі визначаємо за рівнянням (4.3), яке вірне для будь-якого процесу:
Зміну ентальпії в процесі визначаємо за рівнянням (5.5), яке вірне для будь-якого процесу:
Для отримання рівняння зміни ентропії в процесі скористаємося рівнянням (5.8):
З нього при
Питома робота розширення газу в процесі, яка згідно з рівнянням (3.11)
Питоме тепло процесу при сталій теплоємності
тобто при
Графік ізохорного процесу називається ізохорою. В координатах В координатах
   при незмінній температурі, наприклад, у процесі 1–7. З рівняння (5.8) випливає, що ця зміна при при незмінній температурі, наприклад, у процесі 1–7. З рівняння (5.8) випливає, що ця зміна при 
тобто вона дійсно не залежить від температури, а ізохори Рівняння (6.3) вказує на те, що відстань між ізохорами збільшується при зростанні кінцевого об’єму, отже чим більший питомий об’єм газу, тим далі від осі ординат буде знаходитися ізохора.
Ізобарний процес Ізобарним називається процес, що відбувається при незмінному тиску. Зв’язок між основними термодинамічними параметрами газу в цьому процесі можна встановити безпосередньо з рівняння стану ідеального газу:
Отже
тобто, в ізобарному процесі питомий об’єм газу змінюється пропорційно абсолютній температурі. При розширенні газу його температура зростає, при стисканні – зменшується. Зміну внутрішньої енергії газу в процесі визначаємо за рівнянням (4.3), яке вірне для будь-якого процесу:
Зміну ентальпії в процесі визначаємо за рівнянням (5.5), яке вірне для будь-якого процесу:
Зміну ентропії в оборотному ізобарному процесі при сталій теплоємності можна знайти з рівняння (5.10):
З нього при
Питома робота розширення газу в процесі визначається за рівнянням
або
Питоме тепло процесу при сталій теплоємності
тобто при
це означає, що все тепло, підведене в процесі, витрачається на зміну ентальпії газу.
Рис. 6.3. Графіки ізобарних процесів
Графік ізобарного процесу називається ізобарою. В координатах В координатах В координатах
тобто вона дійсно не залежить від температури, а визначається лише величинами тисків та природою газу. Це підтверджує еквідистантність ізобар в координатах З рівняння (6.8) випливає, що при Співставляючи рівняння (6.2) і (6.5) приходимо до висновку, що при виконанні ізохорного та ізобарного процесів у одному й тому ж температурному інтервалі, зміна ентропії буде більшою в ізобарному процесі через те, що завжди
Наслідком цього є те, що в координатах
Ізотермічний процес Ізотермічним називається процес, що відбувається при незмінній температурі. Рівняння цього процесу безпосередньо випливає з рівняння стану ідеального газу:
Отже
тобто при сталій температурі об’єм газу змінюється зворотно пропорційно його тиску. Відповідно до рівнянь (4.3) і (5.5) внутрішня енергія та ентальпія газу в ізотермічному процесі не змінюються, тобто
Зміну ентропії в ізотермічному процесі можна визначити за рівняннями (6.3) або (6.8):
Питома робота розширення газу в процесі визначається за рівнянням
Виразимо в підінтегральному виразі тиск
звідси
Підставляючи знайдене значення в підінтегральний вираз і інтегруючи отримане рівняння, маємо:
З урахуванням (6.9)
Питоме тепло процесу знайдемо за рівнянням першого закону термодинаміки (3.6)
Так як в ізотермічному процесі зміна внутрішньої енергії газу
це означає, що все тепло, підведене до газу в ізотермічному процесі, витрачається ним на виконання зовнішньої роботи розширення. Питоме тепло в ізотермічному процесі можна визначити також за рівнянням
Графік ізотермічного процесу називається ізотермою. В координатах
а) б) Рис. 6.4. Графіки ізотермічного процесу
В координатах
Адіабатний процес Адіабатним називається процес, що відбувається без теплообміну з навколишнім середовищем, тобто тепло цього процесу Для отримання рівняння адіабатного процесу скористаємося рівняннями першого закону термодинаміки – згідно з (5.3) в адіабатному процесі
згідно з (3.7) Враховуючи (4.2) і (5.6), маємо
Розділимо перше з останніх рівнянь на друге:
Як відмічалося раніше, відношення
називається показником адіабати. З урахуванням цього та розділяючи перемінні маємо
Інтегруючи цей вираз, отримуємо
Звідси після потенцірування
Отже, для адіабатного процесу
Враховуючи, що за рівнянням стану ідеального газу
з рівнянь (6.15) отримуємо:
Зміну внутрішньої енергії газу в процесі визначаємо за рівнянням (4.3):
Зміну ентальпії в процесі визначаємо за рівнянням (5.5):
За визначенням елементарна зміна ентропії в процесі
Тому в адіабатному процесі, для якого
Через це оборотний адіабатний процес називають ізоентропним. Роботу розширення в адіабатному процесі можна знайти за рівнянням першого закону термодинаміки:
Беручи до уваги, що в процесі
З цього випливає, що в адіабатному процесі газ виконує роботу за рахунок своєї внутрішньої енергії, тобто при розширенні газу його внутрішня енергія та температура зменшуються. З іншого боку питома робота розширення газу в процесі визначається за рівнянням
Виразимо в підінтегральному виразі тиск
звідси
Підставляючи знайдене значення в підінтегральний вираз і інтегруючи отримане рівняння, маємо:
З урахуванням співвідношень (6.15) і (6.16)
а) б)
Рис. 6.5. Графіки адіабатного процесу
Графік адіабатного процесу називається адіабатою. В координатах Порівнюючи рівняння адіабати (6.14) з рівнянням ізотерми (6.9) приходимо до висновку, що графік адіабати є крутішим у порівнянні з графіком ізотерми через те, що В координатах
Політропні процеси Важливе місце в термодинаміці займають процеси, об’єднуючою ознакою яких є незмінність теплоємності процесу. Ці процеси називаються політропними, що означає закономірні. Встановимо рівняння політропного процесу, для якого теплоємність Для цього скористаємося рівняннями першого закону термодинаміки у формах (5.3) і (3.7), пам’ятаючи, що тепло політропного процесу
Отже
З цих рівнянь маємо:
Розділимо перше з останніх рівнянь на друге:
Позначимо
Цей комплекс називається показником політропного процесу. З урахуванням цього позначення та розділивши перемінні, маємо
Інтегруючи цей вираз, отримуємо
Звідси після потенцірування
Отримане рівняння називається рівнянням політропного процесу. Порівнюючи його з рівнянням адіабатного процесу (6.14) приходимо до висновку, що ці рівняння формально однакові – вони відрізняються лише показником процесу. Через це всі співвідношення між основними параметрами стану, отримані для адіабатного процесу, справедливі також і для політропного процесу після заміни в них показника адіабати
Зміну внутрішньої енергії газу в процесі визначаємо за рівнянням (4.3):
Зміну ентальпії в процесі визначаємо за рівнянням (5.5):
Зміна ентропії в політропному процесі, як і в будь якому іншому
Інтегруючи цей вираз у межах від
Теплоємність політропного процесу знайдемо з рівняння (6.19). З нього випливає:
Враховуючи, що
маємо
Звідси
Тоді з (6.22) для політропного процесу
Робота зміни об’єму, що виконує газ у політропному процесі, визначається за рівняннями, аналогічними рівнянням для адіабатного процесу, тобто
або
Питоме тепло в політропному процесі
або в кінцевому вигляді
Графік політропного процесу називається політропою. Вигляд політропи визначається величиною показника процесу У загальному випадку показник політропи може приймати будь-яке значення з діапазону Отже і теплоємність політропного процесу змінюється в цьому ж діапазоні, тобто Окремими випадками політропних процесів є розглянуті раніше основні термодинамічні процеси. У таблиці 6.1 наведені значення показника політропи та значення теплоємкостей цих процесів.
Таблиця 6.1.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 869; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.251.26 (0.009 с.) |

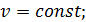


 і
і  –діаграм;
–діаграм;






 випливає
випливає

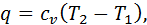
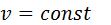
 ,
, це означає, що все тепло, підведене в процесі, витрачається на зміну внутрішньої енергії газу.
це означає, що все тепло, підведене в процесі, витрачається на зміну внутрішньої енергії газу.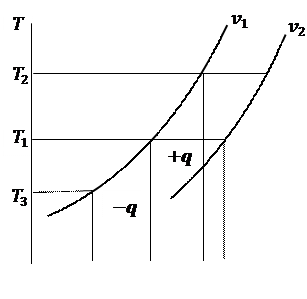
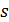

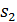



 еквідистантні.
еквідистантні.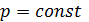



 випливає, що
випливає, що




 ,
,

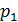
 , а також показані процеси нагрівання 1–2 та охолодження 1–3, що відбуваються при тиску
, а також показані процеси нагрівання 1–2 та охолодження 1–3, що відбуваються при тиску 
 це означає, що в цьому разі ізобара
це означає, що в цьому разі ізобара 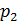 буде знаходитися ліворуч від ізобари
буде знаходитися ліворуч від ізобари  тобто чим більший тиск газу, тим ближчою до осі ординат буде ізобара.
тобто чим більший тиск газу, тим ближчою до осі ординат буде ізобара.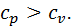






 через питомий об’єм
через питомий об’єм  виходячи з рівняння ізотермічного процесу. Відповідно до цього рівняння
виходячи з рівняння ізотермічного процесу. Відповідно до цього рівняння ,
,


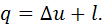
 , то в цьому процесі
, то в цьому процесі

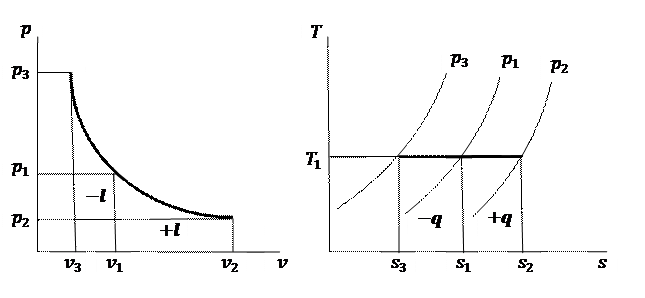
 (рис. 6.3, б). Процес 1–2 на рис. 6.3, б – це процес ізотермічного розширення газу, процес 1–3 – процес ізотермічного стискання газу. Площа 1-2-4-5-1 еквівалентна питомому теплу, яке підводиться до газу при його розширенні, площа 1-3-6-5-1 еквівалентна питомому теплу, яке відводиться від газу при його стисканні.
(рис. 6.3, б). Процес 1–2 на рис. 6.3, б – це процес ізотермічного розширення газу, процес 1–3 – процес ізотермічного стискання газу. Площа 1-2-4-5-1 еквівалентна питомому теплу, яке підводиться до газу при його розширенні, площа 1-3-6-5-1 еквівалентна питомому теплу, яке відводиться від газу при його стисканні.




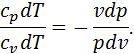

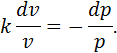
 .
.







 , маємо
, маємо
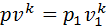 ,
,
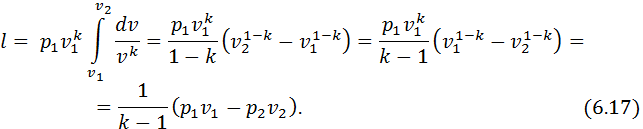



 адіабата відображається нерівнобічною гіперболою відповідно до рівняння (6.14) (рис. 6.3, а). При розширенні газ виконує роботу і температура його зменшується. При стиканні робота виконується над газом і це супроводжується зростанням його температури. На рис. 6.4, а процес 1–2 – це процес адіабатного розширення газу, процес 1–3 – процес адіабатного стискання газу. Площа 1-2-А-B-1 еквівалентна роботі, що виконує газ, площа 1-3-С-B-1 еквівалентна роботі, яка виконується над газом.
адіабата відображається нерівнобічною гіперболою відповідно до рівняння (6.14) (рис. 6.3, а). При розширенні газ виконує роботу і температура його зменшується. При стиканні робота виконується над газом і це супроводжується зростанням його температури. На рис. 6.4, а процес 1–2 – це процес адіабатного розширення газу, процес 1–3 – процес адіабатного стискання газу. Площа 1-2-А-B-1 еквівалентна роботі, що виконує газ, площа 1-3-С-B-1 еквівалентна роботі, яка виконується над газом.
 (рис. 6.3, б). Процес 1–2 на рис. 6.3, б – це процес адіабатного розширення газу, процес 1–3 – процес адіабатного стискання газу.
(рис. 6.3, б). Процес 1–2 на рис. 6.3, б – це процес адіабатного розширення газу, процес 1–3 – процес адіабатного стискання газу.

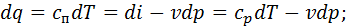






 .
.
 на показник політропного процесу
на показник політропного процесу  Отже, для політропного процесу
Отже, для політропного процесу




 до
до  , знаходимо зміну
, знаходимо зміну  у процесі в кінцевому вигляді:
у процесі в кінцевому вигляді:




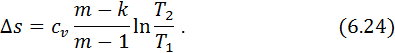
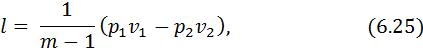




 .
.