Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметри стану ентальпія та ентропіяСодержание книги
Поиск на нашем сайте Важливу роль у різноманітних термодинамічних розрахунках відіграє сума внутрішньої енергії системи Ентальпію будемо позначати Отже, за визначенням ентальпія
Питома ентальпія, тобто ентальпія,що віднесена до 1 кг газу,
Ця нова функція скомбінована лише з параметрів стану, тому й сама є функцією або параметром стану. Ентальпія відноситься до екстенсивних параметрів, через те, що її величина пропорційна масі. Ентальпія вимірюється в тих же одиницях, що і внутрішня енергія, тобто в Дж. Питома ентальпія – у Дж/кг. У більшості випадків вважають, що ентальпія ідеального газу дорівнює нулю при Використовуючи ентальпію можна надати іншого виду аналітичному виразу першого закону термодинаміки. Рівняння першого закону термодинаміки в диференціальній формі
Із очевидного співвідношення
Тоді Отже, рівняння першого закону термодинаміки може бути записане так:
або в кінцевому виді
З отриманого рівняння випливає, що тепло, підведене до газу в процесі зі сталим тиском, тобто при
Але це тепло відповідно до (4.4) Отже
або в диференціальній формі
За рівнянням (5.5) можна підрахувати зміну ентальпії в будь-якому термодинамічному процесі. Фізичний зміст ентальпії проявляється при аналізі газових потоків – вона являє собою повну потенціальну енергію потоку газу. Поява термодинамічної функції ентропія пов’язана з пошуком можливості графічного зображення тепла, що підводиться в термодинамічному процесі. У п. 3.5 з’ясовано, що кількість тепла, підведеного в процесі, залежить від виду процесу. У той же час відношення тепла до температури, при якій воно підводиться, володіє властивістю параметра стану, тобто його зміна не залежить від виду процесу. Покажемо це, позначаючи вказане відношення При безкінечно малій кількості підведеного тепла маємо елементарну зміну
З рівняння стану ідеального газу
а відповідно до (4.2)
тому
Інтегруючи цей вираз у межах від
З отриманого рівняння випливає, що зміна Отриманий параметр стану називається ентропією. Ентропія газу пропорційна його масі, тому це – екстенсивний параметр стану. Повну ентропію позначають Питому ентропію позначають
Вона вимірюється в Дж/(кг∙К). Визначити зміну ентропії в термодинамічному процесі можна не лише за рівнянням (5.8). Підставляючи в (5.7) значення
Враховуючи, що з рівняння стану ідеального газу
а відповідно до (4.4)
маємо
Інтегруючи цей вираз у межах від
У термодинаміці ентропія нерозривно пов’язана з поняттям теплоти: є теплота – є зміна ентропії, немає теплоти – немає зміни ентропії. Отже, значення має лише зміна ентропії. Абсолютна величина ентропії в технічних задачах ніякої фізичної суті не має. У деяких термодинамічних розрахунках для зручності умовно приймають за початок відліку ентропії її значення при нормальних фізичних умовах ( Використовуючи ентропію, елементарне тепло процесу визначають так:
Інтегруючи цей вираз, знаходимо питоме тепло, що підводиться до газу в процесі:
Величина цього тепла визначається видом функції Зміна ентропії однозначно визначає знак теплоти. При збільшенні ентропії Використовуючи поняття ентропії можна графічно показати тепло процесу, побудувавши для цього графік процесу в координатах На рис. 5.1 лінія 1–2 відображає оборотний термодинамічний процес зміни стану термодинамічного тіла. Заштрихована площинка під елементарною ділянкою графіка процесу являє собою елементарну кількість теплоти
Інтегральна сума таких площинок під лінією 1–2 дорівнює повній кількості питомого тепла, що отримує тіло в процесі 1–2:
 Через те, що площа під кривою процесу в координатах Через те, що площа під кривою процесу в координатах  еквівалентна кількості тепла, підведеного в процесі, графік процесу в цій системі координат називають тепловою діаграмою. еквівалентна кількості тепла, підведеного в процесі, графік процесу в цій системі координат називають тепловою діаграмою.
У
 висновок випливає з того, що згідно з правилами аналітичної геометрії величина піддотичної для точки висновок випливає з того, що згідно з правилами аналітичної геометрії величина піддотичної для точки 
При цьому теплоємність додатна, якщо піддотична знаходиться ліворуч від точки, що розглядається, і від’ємна, якщо праворуч. У термодинаміці внутрішню енергію, ентальпію, ентропію називають калоричними властивостями речовини, а тиск, температуру, питомий об’єм – термічними властивостями.
|
||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 620; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.009 с.) |

 та добутку тиску системи
та добутку тиску системи  на величину об’єму системи
на величину об’єму системи  Це стало причиною використання цієї суми як окремої величини, яку було названо ентальпією або тепловмістом. Пізніше був з’ясований фізичний зміст цього поняття.
Це стало причиною використання цієї суми як окремої величини, яку було названо ентальпією або тепловмістом. Пізніше був з’ясований фізичний зміст цього поняття.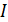 . Використовують також позначення
. Використовують також позначення  .
.








 , витрачається на зміну його ентальпії:
, витрачається на зміну його ентальпії: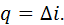
 .
.







 до
до  , знаходимо зміну
, знаходимо зміну  у процесі:
у процесі:
 Одиниця її виміру – Дж/К.
Одиниця її виміру – Дж/К.

 з рівняння (5.3), отримуємо:
з рівняння (5.3), отримуємо: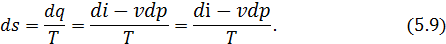


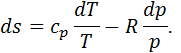

 тобто вважають, що ентропія при цих умовах
тобто вважають, що ентропія при цих умовах  У цьому разі користуються абсолютним значенням ентропії для певного стану, розуміючи під ним різницю ентропії для певного стану і її початкового значення:
У цьому разі користуються абсолютним значенням ентропії для певного стану, розуміючи під ним різницю ентропії для певного стану і її початкового значення: 


 яка залежить від виду процесу. Це є додатковим твердженням того, що теплота – це функція процесу.
яка залежить від виду процесу. Це є додатковим твердженням того, що теплота – це функція процесу. тепло додатне, тобто воно підводиться до системи; при зменшенні ентропії
тепло додатне, тобто воно підводиться до системи; при зменшенні ентропії  тепло від’ємне, тобто воно відводиться від системи.
тепло від’ємне, тобто воно відводиться від системи. Це випливає з того, що інтеграл у рівнянні (5.10) еквівалентний площі, обмеженій цим графіком, віссю
Це випливає з того, що інтеграл у рівнянні (5.10) еквівалентний площі, обмеженій цим графіком, віссю  у крайніх точках процесу).
у крайніх точках процесу). та дорівнює:
та дорівнює:

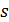
 – діаграмі можна показати графічно також істинну теплоємність для будь-якої точки процесу. Наприклад, для точки
– діаграмі можна показати графічно також істинну теплоємність для будь-якої точки процесу. Наприклад, для точки  , що утворюється дотичною до точки
, що утворюється дотичною до точки  лінією
лінією  та проекцією точки
та проекцією точки