Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ізохорна та ізобарна теплоємність ідеального газуСодержание книги
Поиск на нашем сайте
Виходячи з визначення поняття теплоємності можна стверджувати, що ізохорна теплоємність дорівнює відношенню кількості тепла, підведеного до тіла в процесі при сталому об’ємі, до зміни температури тіла. Зокрема, масову ізохорну теплоємність у диференціальній формі можна визначити так:
З урахуванням рівнянь (3.7) і (3.9) маємо
Але при
або
У кінцевому вигляді, зокрема, маємо
Зважаючи на те, що зміна внутрішньої енергії в термодинамічних процесах не залежить від виду процесу, а визначається лише її величинами у початковому та кінцевому станах, приходимо до висновку, що за рівнянням (4.2) можна підраховувати зміну внутрішньої енергії в будь-якому термодинамічному процесі. Ізобарна теплоємність дорівнює відношенню кількості тепла, підведеного до тіла в процесі при сталому тиску, до зміни температури тіла. Масова ізобарна теплоємність у диференціальній формі визначається так:
Запишемо рівняння стану ідеального газу та продиференцюємо його. Отримуємо
У процесі зі сталим тиском
Тоді з рівняння
Це рівняння називається рівнянням Майєра. Воно встановлює, що для ідеального газу різниця між масовою ізобарною та масовою ізохорною теплоємностями дорівнює газовій сталій. Його широко використовують у термодинамічних розрахунках. Рівняння Майєра можна записати для мольних теплоємностей, помноживши обидві його частини на молекулярну масу газу
У термодинаміці важливою величиною є також відношення масової ізобарної та масової ізохорної тепоємностей, яке називається показником адіабати і позначається
Згідно з класичною молекулярно-кінетичною теорією газів значення їхніх мольних теплоємностей і показника адіабати визначається кількістю ступенів свободи молекули, яка, у свою чергу, залежить від кількості атомів у молекулі, тобто від атомносі газу. У табл. 4.1 наведені значення цих величин, що отримані методами молекулярно-кінетичної теорії.
Таблиця 4.1
Дані табл. 4.1 добре підтверджуються експериментами при порівняно невисоких температурах. При підвищенні температури спостерігається суттєве відхилення наведених у табл. 4.1 величин від експериментально визначених, що свідчить про залежність теплоємності ідеальних газів від температури. Значна розбіжність між теоретичними та експериментально визначеними величинами має місце також при збільшенні кількості атомів у молекулі. Причому останнє спостерігається як при нормальних температурах, так і при підвищених. Теплоємність реальних газів Теплоємність реальних газів залежить у загальному випадку від тиску та температури, тобто
Для газів, стан яких далекий від області насичення, залежність теплоємності від тиску проявляється слабо і на практиці нею часто нехтують. У той же час залежність теплоємності від температури є доволі суттєвою і при точних розрахунках повинна враховуватись. Аналітичний вираз цієї залежності складний і вимагає експериментального визначення ряду констант для кожного газу. Тому теплоємності реальних газів визначають експериментально. Цими експериментами встановлено, що залежність теплоємності реального газу від температури криволінійна (рис. 4.1). Через це існують поняття про істинну та середню теплоємності.
Під істинною теплоємністю
Для реальних газів кожному значенню температури процесу відповідає конкретне значення теплоємності. Визначення теплоти процесу за допомогою істинної теплоємності виконується шляхом інтегрування:
Це тепло еквівалентне площі 1-2-3-4-1 на рис. 4.1. Середньою теплоємністю
При розрахунках в основному користуються середніми теплоємностями, визначаючи теплоту, що підведена до газу в процесі, за формулою:
Сумісно вирішуючи рівняння (4.7) і (4.8) отримуємо
Рівняння (4.8) встановлює зв'язок між середньою та істинною теплоємностями газу в даному процесі. Для точного визначення середньої теплоємності існують спеціальні таблиці, у яких наведені середні ізобарні та ізохорні теплоємності різних газів для інтервалу температур від Відповідно до правил інтегрування, інтеграл у рівнянні (4.6) може бути представленим різницею двох інтегралів:
з якої з урахуванням (4.8) випливає
Враховуючи рівняння (4.7), отримуємо
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1903; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

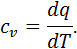
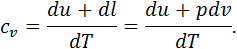
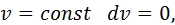 отже в цьому процесі
отже в цьому процесі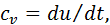 (4.1)
(4.1)
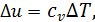 (4.3)
(4.3)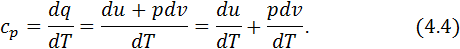
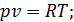
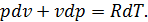
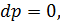 отже для цього процесу
отже для цього процесу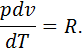
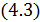 з урахуванням (4.1) маємо:
з урахуванням (4.1) маємо: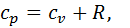 або
або 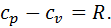 (4.5)
(4.5)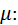
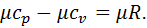
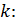
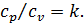 (4.6)
(4.6)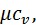 кДж/(кг∙К)
кДж/(кг∙К)
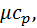 кДж/(кг∙К)
кДж/(кг∙К)
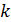

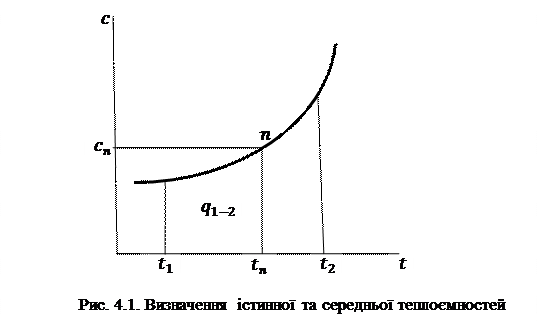
 розуміють фактичне значення теплоємності газу
розуміють фактичне значення теплоємності газу 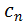 , що відповідає певній температурі
, що відповідає певній температурі 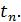 Істинна теплоємність дорівнює відношенню елементарної кількості теплоти, що підводиться до газу в якомусь термодинамічному процесі, до безкінечно малої різниці температур відносно точки процесу з фіксованою температурою:
Істинна теплоємність дорівнює відношенню елементарної кількості теплоти, що підводиться до газу в якомусь термодинамічному процесі, до безкінечно малої різниці температур відносно точки процесу з фіксованою температурою: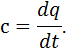

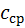 в інтервалі температур від
в інтервалі температур від 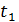 до
до 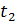 називають відношення кількості теплоти
називають відношення кількості теплоти  , підведеної в певному процесі, до отриманої в процесі різниці температур
, підведеної в певному процесі, до отриманої в процесі різниці температур 

 . (4.8)
. (4.8)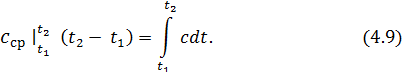
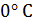 до певної температури
до певної температури  . Визначимо порядок підрахунку за допомогою цих таблиць середньої теплоємності газу для інтервалу між довільними температурами
. Визначимо порядок підрахунку за допомогою цих таблиць середньої теплоємності газу для інтервалу між довільними температурами 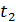 .
.