
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос№4. Силовые линии электрического поля. Поток вектора. Электрическая теорема Гаусса и ее применение для расчетов полей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, условились проводить их с определенной густотой. Число линий напряженности, пронизывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Величина Поток вектора напряженности сквозь сферическую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре Этот результат справедлив для замкнутой поверхности любой формы. Таким образом, для поверхности любой формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на Рассмотрим применение теоремы Гаусса к расчету некоторых электростатических полей в вакууме: Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость заряжена с постоянной поверхностной плотностью Поле двух бесконечных параллельных разноименно заряженных плоскостей Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью ( При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда. Если r' < R, тo замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (Е = 0). Поле объемно заряженного шара. Напряженность поля вне равномерно заряженного шара описывается формулой: а внутри его изменяется линейно с расстоянием
Вопрос№5.Работа электрического поля. Теорема о циркуляции напряженности электрического поля. Потенциал. Эквипотенциальная поверхность. Связь потенциала с напряженностью. Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд Работа силы
Так как Работа при перемещении заряда
не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т. е.
Силовое поле, обладающее свойством
называется потенциальным. Интеграл, стоящий в левой части соотношения наз. циркуляцией вектора Е вдоль замкнутого контура L. Итак, циркуляция вектора напряженности электростатического поля точечного заряда q вдоль произвольного замкнутого контура проведенного в поле, равна нулю. Условие является необходимым и достаточным для того, чтобы поле напряженностью Е было потенциальным. Формула
справедлива только для электростатического поля.
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 864; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.01 с.) |

 . Тогда число линий напряженности, пронизывающих элементарную площадку dS, нормаль
. Тогда число линий напряженности, пронизывающих элементарную площадку dS, нормаль  которой образует угол
которой образует угол  с вектором
с вектором 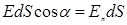 , где
, где  – проекция вектора
– проекция вектора  называется потоком вектора напряженности через площадку dS. Единица потока вектора напряженности электростатического поля 1
называется потоком вектора напряженности через площадку dS. Единица потока вектора напряженности электростатического поля 1  . Для произвольной замкнутой поверхности S поток вектора
. Для произвольной замкнутой поверхности S поток вектора  , где интеграл берется по замкнутой поверхности S.
, где интеграл берется по замкнутой поверхности S. .
. , т. е.
, т. е. 
 .
. (
( – заряд приходящийся на единицу поверхности). Согласно теореме Гаусса,
– заряд приходящийся на единицу поверхности). Согласно теореме Гаусса,  , откуда
, откуда 
 . Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. Таким образом, результирующая напряженность поля в области между плоскостями описывается формулой
. Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. Таким образом, результирующая напряженность поля в области между плоскостями описывается формулой  , а вне объема, ограниченного плоскостями, равна нулю.
, а вне объема, ограниченного плоскостями, равна нулю.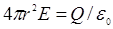 откуда
откуда 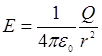
 ).
).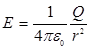 (
( согласно выражению
согласно выражению  (
(
 ).
). , то сила, приложенная к заряду, совершает работу.
, то сила, приложенная к заряду, совершает работу.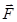 на элементарном перемещении dl равна
на элементарном перемещении dl равна .
. , то
, то  .
.
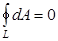 .
. ,
,



