
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Криптоаналіз блочних та потокових шифрів.Содержание книги
Поиск на нашем сайте
Найбільш поширеними видами криптоаналізу блокових шифрів є диференціальний і лінійний криптоаналіз. Диференціальний криптоаналіз Поняття диференціального криптоаналізу було введено Елі Біхамом (Biham) і Аді Шамір (Shamir) у 1990 році. Кінцева завдання диференціального криптоаналізу - використовуючи властивості алгоритму, в основному властивості S-box, визначити з'єднання раунду. Конкретний спосіб диференціального криптоаналізу залежить від розглянутого алгоритму шифрування. Якщо в основі алгоритму лежить мережа Фейштеля, то можна вважати, що блок m складається з двох половин - m0 і m1. Диференціальний криптоаналіз розглядає відмінності, які відбуваються в кожній половині при шифруванні. (Для алгоритму DES "відмінності" визначаються за допомогою операції XOR, для інших алгоритмів можливий інший спосіб). Вибирається пара незашифрованих текстів з фіксованим відзнакою. Потім аналізуються відмінності, що вийшли після шифрування одним раундом алгоритму, і визначаються ймовірності різних ключів. Якщо для багатьох пар вхідних значень, що мають одне і те ж відмінність Х, при використанні одного і того ж підключа однаковими (Y) виявляються і відмінності відповідних вихідних значень, то можна говорити, що Х тягне Y з певною ймовірністю. Якщо ця ймовірність близька до одиниці, то можна вважати, що з'єднання раунду знайдений з даною ймовірністю. Так як раунди алгоритму незалежні, ймовірності визначення підключа кожного раунду слід множити. Вважається, що результат шифрування даної пари відомий. Результати диференціального криптоаналізу використовуються як при розробці конкретних S-box, так і при визначенні оптимального числа раундів. Лінійний криптоаналіз Іншим способом криптоаналізу є лінійний криптоаналіз, який використовує лінійні наближення перетворень, виконуваних алгоритмом шифрування. Даний метод дозволяє знайти ключ, маючи достатньо велике число пар (незашифрований текст, зашифрований текст). Розглянемо основні принципи, на яких базується лінійний криптоаналіз. Позначимо P [1],..., P [n] - незашифрований блок повідомлення. C [1],..., C [n] - зашифрований блок повідомлення. K [1],..., K [m] - ключ. A[i, j, …, k] = A[i]⊕A[j]⊕ …⊕A[k]. Метою лінійного криптоаналізу є пошук лінійного рівняння виду P[α1, α2, …, αa] ⊕C[β1, β2, …, βb ] = K[γ1, …, γc] Запускається з ймовірністю р ≠ 0.5. αi, βi і γi - фіксовані позиції в блоках повідомлення та ключі. Чим більше р. відхиляється від 0.5, тим більш відповідним вважається рівняння. Це рівняння означає, що якщо виконати операцію XOR над деякими бітами незашифрованого повідомлення і над деякими бітами зашифрованого повідомлення, вийде біт, що представляє собою XOR деяких бітів ключа. Це називається лінійним наближенням, яке може бути вірним з ймовірністю р. Рівняння складаються наступним чином. Обчислюються значення лівої частини для великого числа пар відповідних фрагментів незашифрованого і зашифрованого блоків. Якщо результат виявляється дорівнює нулю більш ніж у половині випадків, то вважають, що K [γ1,..., γс] = 0. Якщо в більшості випадків виходить 1, вважають, що K [γ1,..., γс] = 1. Таким чином отримують систему рівнянь, рішенням якої є ключ. Як і у випадку диференціального криптоаналізу, результати лінійного криптоаналізу повинні враховуватися при розробці алгоритмів симетричного шифрування. При розгляді методів криптоаналізу потокових шифрів всі методи можна умовно розділити на три класи: силові; статистичні; аналітичні атаки. До силовим атакам відносяться атаки, засновані на принципі повного перебору всіх можливих комбінацій ключа (атака «грубою силою»); при розробці схем шифрування розробники прагнуть до того, щоб при спробі розтину кріптосхеми даний вид атак був найбільш ефективним в порівнянні з іншими передбачуваними видами атак. До статистичним атакам відносяться атаки, засновані на оцінці статистичних властивостей гами шифрувальної (статистичний криптоаналіз). До аналітичних атакам відносять атаки, в яких алгоритм побудови атаки заснований на аналітичних принципах розтину криптосхеми. Силові атаки До цього класу належать атаки, здійснюють повний перебір всіх можливих варіантів. Складність повного перебору залежить від кількості всіх можливих рішень завдання (зокрема, розміру простору ключів або простору відкритих текстів). Цей клас атак застосуємо до всіх видів систем потокового шифрування. При розробці систем шифрування розробники прагнуть зробити так, щоб цей вид атак був найбільш ефективним в порівнянні з іншими існуючими методами злому. Статистичні атаки Статистичні атаки діляться на два підкласи: метод криптоаналізу статистичних властивостей шифрувальної гами: спрямований на вивчення вихідний послідовності криптосистеми; криптоаналітик намагається встановити значення наступного біта послідовності з імовірністю вище ймовірності випадкового вибору за допомогою різних статистичних тестів. метод криптоаналізу складності послідовності: криптоаналітик намагається знайти спосіб генерувати послідовність, аналогічну гамі, але більш просто реалізованим способом. Обидва методи використовують принцип лінійної складності. Аналітичні атаки Цей вид атак розглядається в припущенні, що криптоаналітик відомі опис генератора, відкритий і відповідний закритий тексти. Завдання криптоаналітик визначити використаний ключ (початкове заповнення регістрів). Види аналітичних атак, які застосовуються до синхронним потоковим шифрам: кореляційні компроміс "час-пам'ять" інверсійна "Припускай і визначай" на ключову завантаження і реініціалізацію XSL-атака Кореляційні атаки Є найбільш поширеними атаками для злому потокових шифрів. Відомо, що робота по розкриттю криптосистеми може бути значно скорочена, якщо нелінійна функція пропускає на вихід інформацію про внутрішні компонентах генератора. Тому для відновлення початкового заповнення регістрів кореляційні атаки досліджують кореляцію вихідний послідовності шіфросістеми з вихідною послідовністю регістрів. Існують наступні підкласи кореляційних атак: Базові кореляційні атаки Атаки, засновані на низько-вагових перевірках парності Атаки, засновані на використанні сверточних кодів Атаки, що використовують техніку турбо кодів Атаки, засновані на відновленні лінійних поліномів Швидкі кореляційні атаки. Компроміс «час-пам'ять» Мета даної атаки - відновлення початкового стану регістра зсуву (знаходження ключа), використовуючи відому схему пристрою та фрагмент шифрувальної послідовності. Складність атаки залежить від розміру шифру і довжини перехопленої гами. Складається з двох етапів: побудова великого словника, в якому записані всілякі пари «стан-вихід»; припущення про початковий заповненні регістра зсуву, генерація виходу, перегляд перехопленої вихідний послідовності і пошук відповідності зі сгенерованими виходом. Якщо сталася збіг, то дане можливе заповнення з великою ймовірністю є початковим. Прикладами цього класу атак є атака Стіва Беббідж і атака Бірюкова-Шаміра. «Припускай і визначай» Атака грунтується на припущенні, що криптоаналітик відомі гамма, поліном зворотного зв'язку, кількість зрушень регістра між виходами схеми і фільтруюча функція. Складається з трьох етапів: припущення про заповнення деяких осередків регістру; визначення повного заповнення регістра на підставі припущення про знання криптоаналітик; генерація вихідний послідовності; якщо вона збігається з гамою, то припущення на першому етапі було вірно, якщо не збігається, то повертаємося до етапу 1. Складність алгоритму залежить від пристрою генератора і від кількості припущень. Асиметрична криптографія. Асиметрична криптографія спочатку задумана як засіб передачі повідомлень від одного об'єкта до іншого (а не для конфіденційного збереження інформації, яку забезпечують тільки симетричні алгоритми). Тому подальше пояснення ми будемо вести в термінах "відправник" - особа, шифрує, а потім відправляє інформацію по незахищеному каналу і "одержувач" - особа, що приймає і відновлює інформацію в її початковому вигляді. Основна ідея асиметричних криптоалгоритмів полягає в тому, що для шифрування повідомлення використовується один ключ, а при дешифруванні - інший. Крім того, процедура шифрування обрана так, що вона необоротна навіть за відомим ключу шифрування - це друга необхідна умова асиметричної криптографії. Тобто, знаючи ключ шифрування і зашифрований текст, неможливо відновити вихідне повідомлення - прочитати його можна тільки за допомогою другого ключа - ключа дешифрування. А раз так, то ключ шифрування для відправки листів будь-якій особі можна взагалі не приховувати - знаючи його все одно неможливо прочитати зашифроване повідомлення. Тому, ключ шифрування називають в асиметричних системах "відкритим ключем", а ось ключ дешифрування одержувачу повідомлень необхідно тримати в секреті - він називається "закритим ключем". Напрошується питання: "Чому, знаючи відкритий ключ, не можна обчислити закритий ключ?" - Це третя необхідна умова асиметричної криптографії - алгоритми шифрування і дешифрування створюються так, щоб знаючи відкритий ключ, неможливо обчислити закритий ключ. У цілому система листування при використанні асиметричного шифрування виглядає наступним чином. Для кожного з N абонентів, що ведуть листування, обрана своя пара ключів: "відкритий" Ej і "закритий" Dj, де j - номер абонента. Всі відкриті ключі відомі всім користувачам мережі, кожен закритий ключ, навпаки, зберігається тільки у того абонента, якому він належить. Якщо абонент, скажімо під номером 7, збирається передати інформацію абоненту під номером 9, він шифрує дані ключем шифрування E9 і відправляє її абоненту 9. Незважаючи на те, що всі користувачі мережі знають ключ E9 і, можливо, мають доступ до каналу, по якому йде зашифроване послання, вони не можуть прочитати вихідний текст, так як процедура шифрування незворотна по відкритому ключу. І тільки абонент № 9, отримавши послання, здійснює над ним перетворення за допомогою відомого тільки йому ключа D9 і відновлює текст послання. Зауважте, що якщо повідомлення потрібно відправити у протилежному напрямку (від абонента 9 до абоненту 7), то потрібно буде використовувати вже іншу пару ключів (для шифрування ключ E7, а для дешифрування - ключ D7). Як ми бачимо, по-перше, в асиметричних системах кількість існуючих ключів пов'язано з кількістю абонентів лінійно (у системі з N користувачів використовуються 2 * N ключів), а не квадратично, як у симетричних системах. По-друге, при порушенні конфіденційності k-ої робочої станції зловмисник дізнається лише ключ Dk: це дозволяє йому читати всі листи, що надходять абоненту k, але не дозволяє видавати себе за нього при відправці листів. Алгоритм RSA стоїть біля витоків асиметричної криптографії. Він був запропонований трьома дослідниками-математиками Рональдом Рівестом (R. Rivest), Аді Шамір (A. Shamir) і Леонардом Адльманом (L. Adleman) в 1977-78 роках. Першим етапом будь-якого асиметричного алгоритму є створення пари ключів: відкритого та закритого і поширення відкритого ключа "по всьому світу". Для алгоритму RSA етап створення ключів складається з наступних операцій: Вибираються два прості (!) Числа p і q Обчислюється їх добуток n (= p * q) Вибирається довільне число e (e <n), таке, що НОД (e, (p-1) (q-1)) = 1, тобто e повинно бути взаємно простим з числом (p-1) (q-1). Методом Евкліда вирішується в цілих числах (!) Рівняння e * d + (p-1) (q-1) * y = 1. Тут невідомими є змінні d і y - метод Евкліда як раз і знаходить безліч пар (d, y), кожна з яких є рішенням рівняння в цілих числах. Два числа (e, n) - публікуються як відкритий ключ. Число d зберігається в найсуворішому секреті - це і є закритий ключ, який дозволить читати всі послання, зашифровані за допомогою пари чисел (e, n). Метод Райвеста-Шамира-Адлемана (RSА). RSA багато років протистоїть інтенсивному криптоаналізу. Крипостійкість заснована на трудомісткості розкладання на множники (факторизації) великих чисел. Відкритий і секретний ключі є функціями двох великих (100 ~ 200 двійкових розрядів або навіть більше) простих чисел. Передбачається, що завдання відновлення відкритого тексту по шифротексту та відкритому ключу еквівалентна задачі факторизації. Для генерації пари ключів беруться два великих випадкових простих числа p та q. З метою максимальної крипостійкості p і q вибираються рівної довжини. Потім обчислюється їх добуток n = p*q (n називається модулем). Далі випадковим чином вибирається число e (ключ шифрування), що задовольняє умові: 1 <e <(p - 1) * (q - 1) і не має спільних дільників окрім 1 (взаємно просте) з числом f(n)=(p-1)*(q-1). Нарешті розширений алгоритм Евкліда використовується для обчислення ключа дешифрування d, такого, що ed = 1 mod f(n). Число d таке, що (ed - 1) ділиться на (p - 1) (q-1). Відкритий ключ (Public): n- добуток двух простих чисел p і q (повинні зберігатися в секреті); e - число, взаємно просте з f(n) Секретний ключ (Private): d = e-1mod f(n) Шифрування: c = me mod n Дешифрування: m = cd mod n Числа d і n - також взаємно прості числа. Числа e і n - відкритий ключ, а d - секретний. Два простих числа p і q зберігаються в секреті. Для шифрування повідомлення m необхідно виконати його розбивку на блоки, кожний з яких менше n (для двійкових даних вибирається найбільша ступінь числа 2, менша n). Тобто якщо p і q - 100 розрядні прості числа, то n буде містити близько 20 розрядів і кожен блок повідомлення mi повинен мати таке ж число розрядів. Якщо ж потрібно зашифрувати фіксоване число блоків, їх можна доповнити декількома нулями зліва, щоб гарантувати, що блоки завжди будуть менше n. Зашифроване повідомлення c складатиметься з блоків ci тієї ж самої довжини. Шифрування зводитися до обчислення: ci=mie mod n. При дешифруванні для кожного зашифрованого блоку ci обчислюється mi = cid mod n Останнє справедливо, так як cid = (mie)d = mied = mik f (n)+1 = mi · 1 = mi Всі обчислення виконуються за mod n. Повідомлення може бути зашифроване за допомогою d, а дешифровано за допомогою e, можливий будь-який вибір. Передбачається, що крипостійкість RSA залежить від проблеми розкладання на множники великих чисел. Проте ніколи не було доведено математично, що потрібно n розкласти на множники. Щоб відновити m по с та e. Не виключено, що може бути відкритий зовсім інший спосіб криптоаналізу RSA. Однак, якщо цей новий спосіб дозволить криптоаналітику отримати d, він також може бути використаний для розкладання на множники великих чисел. Також можна атакувати RSA, вгадавши значення (p-1) (q-1). Однак цей метод не простіше розкладання n на множники. При використанні RSA розкриття навіть кількох бітів інформації з шифротексту не легше, ніж дешифрування всього повідомлення. Самою очевидною атакою на RSA є розкладання n на множники. Будь-який супротивник зможе отримати відкритий ключ e та модуль n. Щоб знайти ключ дешифрування d, супротивник повинен розкласти n на множники. Криптоаналітик може перебирати всі можливі d, поки не підбере правильне значення. Але подібна силова атака навіть менш ефективна, ніж спроба розкладання n на множники. У 1993 р. був запропонований метод криптоаналізу, заснований на малій теоремі Ферма. На жаль, цей метод виявився повільнішим за розкладання на множники. Існує ще одна проблема. Більшість загальноприйнятих тестів встановлює простоту числа з певною ймовірністю. Що станеться якщо p або q виявиться складовим? Тоді у модуля n буде три або більше дільників. Відповідно деякі дільники будуть менше рекомендованої величини, що, у свою чергу відкриває можливості для атаки шляхом факторизації модуля. Інша небезпека полягає в генерації псевдопростих чисел (чисел Кармайкла), що задовольняють тестам на простоту, але при цьому не є простими. Однак імовірність генерації таких чисел пренебрежимо мала. На практиці, послідовно застосовуючи набір різних тестів на простоту, можна звести ймовірність генерації складеного числа до необхідного мінімуму. 19. Перевірка чисел на взаємну простоту (розширений алгоритм Евкліда). Теореми Міллера-Рабіна та Ферма. Пусть а и b - натуральные числа, а d – их наибольший общий делитель. Расширенный алгоритм Эвклида подсчитывает не только d, но и два целых числа α и β таких, что α×а + β×b = d. (1) Отметим, что (за исключением нескольких тривиальных случаев) если α оказывается положительным, то β - отрицательное, и наоборот. Приводимый здесь вариант расширенного алгоритма Эвклида принадлежит Кнуту, автору знаменитой книги «Искусство программирования». Напомним, что алгоритм Эвклида состоит из последовательности делений с остатком. Наибольший общий множитель представляет собой последний ненулевой остаток в этой последовательности. Значит, нам надо найти способ записывать последний ненулевой остаток в виде (1). Предположим, что для вычисления наибольшего общего делителя чисел а и b мы выполнили последовательность делений. Перепишем ее, сопровождая каждую операцию записью предполагаемого представления остатка:
а = bql + rl и rl = ax1 + by1; b = rlq2 + r2 и r2 = ax2 + by2; rl = r2q3 + r3 и r3 = ax3 + by3; r2 = r3q4 + r4 и r4 = ax4 + by4; ............................ (2) rn-3 = rn-2qn-1 + rn-1 и rn-1 = axn-1 + byn-1; rn-2 = rn-1qn-2 и rn = 0. Числа x1,..., xn-1 и у1,..., уn-1 мы b хотим определить. Необходимую информацию удобно свести в таблицу:
Отметим прежде всего, что таблица начинается с двух строчек, которым в ней не следовало бы быть. Действительно, стоящие в первом столбце этих строк числа не являются остатками в каких-либо операциях деления. Мы даем этим строчкам номера -1 и 0, подчеркивая тем самым их «незаконность». Вскоре мы обоснуем их необходимость. Что же мы хотим сделать? Мы хотим заполнить столбцы х и у. Предположим на минуту, что мы получили таблицу заполненной до некоторой, скажем до (j -1)-ой, строки. Для заполнения j -ой строки необходимо прежде всего разделить rj-2 на rj-l. В результате получатся rj и qj - первые два элемента j -ой строки. Не будем забывать, что rj-2 = rj-lqj + rj и 0 ≤ rj < rj-l. Таким образом, rj = rj-2 - rj-lqj. (3) Из строчек j - 1 и j - 2 мы можем взять значения xj-2, xj-l, yj-2 и yj-l. Можно записать rj-2 = aхj-2 + bуj-2 и rj-l = aхj-l + byj-l. Подставляя эти значения в (3), получаем rj = (aхj-2 + byj-2) - (aхj-l + bуj-l)qj = a(хj-2 - qjхj-l) + b(yj-2 - qjyj-l). Поэтому xj = xj-2 - qjxj-l и yj = yj-2 - qjyj-l . Заметим, что для вычисления хj и yj нам понадобились только частное qj и данные из двух строк таблицы, непосредственно предшествующих j -ой. Вот почему алгоритм Кнута такой эффективный. Для заполнения очередной строки достаточно знать две строчки, непосредственно предшествующие ей; все остальные строчки хранить не обязательно. Итак, мы получили рекуррентную процедуру. Все, что необходимо - это научиться ее запускать. Именно для этого мы и добавили в таблицу две «незаконные» строки. Найти в них значения х и у очень просто. Придавая им тот же смысл, что и в остальных строках, мы должны получить а = ax-l + by-l и b = ах0 + bу0. Поэтому можно просто положить x-l = 1, y-l = 0, х0 = 0 и у0 = 1, и процедуру можно запускать. В результате цепочки делений с остатком мы получим равенство НОД(а, b) = rn-l и вычислим такие целые числа xn-l и yn-l, что d = rn-l = axn-l + byn-l. Значит α = xn-l и β = yn-l Заметим, что, зная а и d = rn-l, мы можем найти β по формуле β = (d - aα)/b. Поэтому достаточно вычислять только первые три столбца таблицы. Приведем численный пример. Если а = 1234 и b = 54, то (полная) таблица выглядит так:
Поэтому α = -7, β = 160 и (-7)×1234 + 160×54 = 2. Теорема Ферма Теорему Ферма часто также называют «малой теоремой Ферма». Она гласит, что если р – простое число, а а – любое целое, то р делит ар – а. Частный случай этой теоремы известен уже сотни лет, но Фермабыл первым, кто доказал теорему в полной общности. Начнем с перевода формулировки теоремы на язык сравнений. Теорема Ферма. Пусть р - положительное простое число и а - целое; тогда ар = а (mod р). Теорема Ферма. Пусть р – положительное простое число, а а - целое, не делящееся на р; то есть Тем не менее, существуют составные числа, относительно которых тест Ферма выдаст ответ «правдоподобно простое», длявсех взаимно простых с п оснований а. Такие числа называются числами Кармайкла. К сожалению, их бесконечно много. Первые из них — это 561, 1105 и 1729. Числа Кармайкла обладают следующими свойствами: они нечетны, имеют по крайней мере три простых делителя, если р делит число Кармайкла n, то р - 1 делит n - 1. Чтобы получить представление об их распределении, посмотрим на числа, не превосходящие 1016. Среди них окажется примерно 2,7×1014 простых чисел, но только 246683≈2,4×105 чисел Кармайкла. Следовательно, они встречаются не очень часто, но и не настолько редко, чтобы их можно было игнорировать. Пример: P=13; a=3 312mod13=531441mod13=1 P=13; a=5 512mod13=244140625mod13=1 P=13; a=7 712mod13=13841287201mod13=1 P=13; a=11 1112mod13=3138428376721mod13=1 Тест Миллера - Рабина Пусть n > 0 – нечетное целое. Выберем целое число b, удовлетворяющее неравенству 1 < b < n - 1, и назовем его основанием. Поскольку n - нечетное, n - 1 должно быть четным числом. Первый шаг теста Миллера состоит в определении такого показателя k ≥ 1, для которого n -1 = 2kq, где q не делится на 2. Иначе говоря, мы должны найти наибольшую степень двойки, делящую n - 1, и соответствующее частноe q. Далее тест вычисляет вычеты по модулю n у следующей последовательности степеней: bq, b2q,..., Разберемся, какими свойствами обладает эта последовательность в случае простого n. Итак, пока не будет оговорено особо, n - простое число. Теорема Ферма говорит нам, что
3начит, если n - простое, то последний вычет в последовательности всегда равен 1. Конечно, единица среди вычетов может встретиться и раньше. Последовательность вычетов, используемая в тесте Миллера, довольно легко вычисляется, потому что каждый вычет (за исключением первого) – квадрат предыдущего. Отсюда вытекает, что как только в последовательности вычетов по модулю n встретится n - 1, все остальные вычеты будут равны 1. Пример: p=13 p-1=12=22*3 – разложение числа р по степеням двойки. b=3
Невозможно определить тип числа. b=5
Число р – простое, так как остаток перед единицей равен р-1. b=7
Число р – простое, так как остаток перед единицей равен р-1. b=11
Число р – простое, так как остаток перед единицей равен р-1. Зламування криптограм RSА. RSA - криптографічна система відкритого ключа, що забезпечує такі механізми захисту як шифрування і цифровий підпис (автентифікація - встановлення автентичності). Криптосистема RSA розроблена в 1977 році і названа на честь її розробників Ronald Rivest, Adi Shamir і Leonard Adleman. Алгоритм RSA працює наступним чином: беруться два досить великих простих числа p і q та обчислюється їх добуток n = p * q; n називається модулем. Потім вибирається число e, що задовольняє умові 1 <e <(p - 1) * (q - 1) і не має спільних дільників окрім 1 (взаємно просте) з числом (p - 1) * (q - 1). Потім обчислюється число d таким чином, що (e * d - 1) ділиться на (p - 1) * (q - 1). e - відкритий (public) показник d - приватний (private) показник. (n; e) - відкритий (public) ключ (n; d). - Приватний (private) ключ. Дільники (фактори) p і q можна або знищити або зберегти разом з приватним (private) ключем. Якби існували ефективні методи розкладання на співмножники (факторингу), то, розклавши n на співмножники (фактори) p і q, можна було б отримати приватний (private) ключ d. Таким чином надійність криптосистеми RSA заснована на важко вирішуваній - практично не вирішуваній - завдання розкладання n на співмножники (тобто на неможливості факторингу n) так як в даний час ефективного способу пошуку співмножників не існує. Припустимо, Аліса хоче послати Бобу повідомлення M. Аліса створює зашифрований текст З, зводячи повідомлення M в ступінь e і множачи на модуль n: C = M**e* (mod n), де e та n - відкритий (public) ключ Боба. Потім Аліса посилає С (зашифрований текст) Бобу. Щоб розшифрувати отриманий текст, Боб зводить отриманий зашифрований текст C в ступінь d і примножує на модуль n: M = c**d*(mod n); залежність між e і d гарантує, що Боб вирахує M вірно. Так як тільки Боб знає d, то лише він має можливість розшифрувати отримане повідомлення. Існує кілька способів злому RSA. Найбільш ефективна атака - знайти секретний ключ, відповідний необхідного відкритому ключу. Це дозволить нападаючому читати всі повідомлення, зашифровані відкритим ключем, і підробляти підпис. Таку атаку можна провести, знайшовши головні співмножники (фактори) загального модуля n - p і q. На підставі p, q і e (загальний показник) нападаючий може легко обчислити приватний показник d. Основна складність в пошуку головних співмножників (факторинг) n. Безпека RSA залежить від розкладання на співмножники (факторингу), що є важким завданням, що не має ефективних способів вирішення. Фактично, завдання відновлення секретного ключа еквівалентна задачі розкладання на множники (факторингу) модуля: можна використовувати d для пошуку співмножників n, і навпаки, можна використовувати n для пошуку d. Треба відзначити, що удосконалення обчислювального обладнання саме по собі не зменшить стійкість криптосистеми RSA, якщо ключі будуть мати достатню довжину. Фактично ж вдосконалення обладнання збільшує стійкість криптосистеми. Інший спосіб зламати RSA полягає в тому, щоб знайти метод обчислення кореня ступеня e з mod n. Оскільки С = Me mod n, то коренем ступеня e з mod n є повідомлення M. Обчисливши корінь, можна розкрити зашифровані повідомлення й підробляти підписи, навіть не знаючи приватний ключ. Така атака не еквівалентна факторингу, але в даний час невідомі методи, які дозволяють зламати RSA таким чином. Однак в особливих випадках, коли на основі одного і того ж показника відносно невеликий величини шифрується досить багато пов'язаних повідомлень, є можливість розкрити повідомлення. Згадані атаки - єдині способи розшифрувати всі повідомлення, зашифровані даними ключем RSA. Існують і інші типи атак, що дозволяють, однак, розшифрувати лише одне повідомлення і не дозволяють нападнику розкрити інші повідомлення, зашифровані тим же ключем. Також вивчалася можливість розшифрування частини зашифрованого повідомлення. Найпростіше напад на окреме повідомлення - атака по передбачуваному відкритому тексту. Нападник, маючи зашифрований текст, передбачає, що повідомлення містить якийсь певний текст, потім шифрує передбачуваний текст відкритим ключем одержувача і порівнює отриманий текст з наявним зашифрованим текстом. Таку атаку можна запобігти, додавши в кінець повідомлення кілька випадкових бітів. Інша атака на єдине повідомлення застосовується в тому випадку, якщо відправник посилає одне і те ж повідомлення M трьом кореспондентам, кожен з яких використовує загальний показник e = 3. Знаючи це, нападаючий може перехопити ці повідомлення і розшифрувати повідомлення M. Таку атаку можна запобігти, вводячи перед кожним шифруванням у повідомлення кілька випадкових бітів. Також існують кілька атак по зашифрованому тексту (або атаки окремих повідомлень з метою підробки підпису), при яких нападаючий створює деякий зашифрований текст і отримує відповідний відкритий текст, наприклад, змушуючи обманним шляхом зареєстрованого користувача розшифрувати підроблене повідомлення. Зрозуміло, існують і атаки, націлені не на криптосистему безпосередньо, а на вразливі місця всієї системи комунікацій в цілому. Такі атаки не можуть розглядатися як злом RSA, так як говорять не про слабкість алгоритму RSA, а скоріше про уразливість конкретної реалізації. Наприклад, нападаючий може заволодіти секретним ключем, якщо той зберігається без належної обережності. Необхідно підкреслити, що для повного захисту недостатньо захистити виконання алгоритму RSA і прийняти заходи математичної безпеки, тобто використовувати ключ достатньої довжини, так як на практиці найбільший успіх мають атаки на незахищені етапи управління ключами системи RSA. Дискретне логарифмування. Стійкість широко розповсюджених у даний час схем ЕЦП (електронний цифровий підпис) заснована на складності рішення завдання дискретного логарифмування в простому полі GF (p). Завдання це формулюється наступним чином: задані прості числа p, q і натуральне число g <p порядку q, тобто gq º 1 (mod p); знаючи значення y = gx (mod p), необхідно знайти x Î Z. В даний час найбільш швидким алгоритмом рішення загальної задачі дискретного логарифмування (при довільному виборі g) є алгоритм узагальненого решета числового поля, обчислювальна складність якого оцінюється як O(exp((c+O(1))(ln (p))1/3(ln (ln (p)))2/3 операцій в полі GF(p), де c» (64/9)1/3. Прогрес в галузі вирішення задачі дискретного логарифмування привів до того, що стала можлива реальна компрометація схем ЕЦП, заснованих на складності обчислень у мультиплікативної групи поля, з боку порушника, який володіє досить невисокими обчислювальними і фінансовими ресурсами. Тому на рубежі XX і XXI століття в багатьох країнах світу стали використовуватися схеми формування ЕЦП, засновані на складності розв'язання задачі дискретного логарифмування в групі точок еліптичної кривої. Це завдання формулюється наступним чином: задана еліптична крива E над полем GF (p), де p - просте число; обрана точка G, що має простий порядок q в групі точок кривої E; знаючи точку kG необхідно відновити натуральне число k.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.245.152 (0.012 с.) |

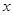






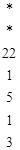
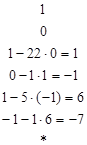

 тогда ap-1 = 1 (mod р).
тогда ap-1 = 1 (mod р). ,
, 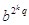 .
.


