
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні поняття криптології. Шифрування та кодування. Стеганографія та криптографія. Алгоритми та протоколиСодержание книги
Поиск на нашем сайте
Прикладная криптология Основні поняття криптології. Шифрування та кодування. Стеганографія та криптографія. Алгоритми та протоколи Криптология - наука, занимающаяся методами шифрования и дешифрования. Криптология состоит из двух частей — криптографии и криптоанализа. Криптография занимается разработкой методов шифрования, а криптоанализ занимается оценкой сильных и слабых сторон методов шифрования, разработкой методов, позволяющих взламывать криптосистемы. Шифрова́ние — преобразование информации в целях сокрытия от неавторизованных лиц, с предоставлением, в это же время, авторизованным пользователям доступа к ней. Кодирование — процесс преобразования сигнала из формы, удобной для использования, в форму, удобную для передачи, хранения, автоматической переработки. Дешифрование – процесс обратный шифрованию. Шифр – совокупность заранее оговоренных способов преобразования исходного секретного сообщения с целью его защиты. Симметричные шифры — способ шифрования, в котором для шифрования и расшифровывания применяется один и тот же криптографический ключ. · Потоковые (т. е. каждый бит исходной информации шифруется независимо от других с помощью гаммирования): o С одноразовым или бесконечным ключом (infinite-key cipher); o С конечным ключом (система Вернама - Vernam); o На основе генератора псевдослучайных чисел (ПСЧ). · Блочные (шифрование данных поблочно): o Шифры перестановки - переставляют элементы открытых данных (биты, буквы, символы) в некотором новом порядке. o Шифры замены - заменяют элементы открытых данных на другие элементы по определенному правилу, и разделяются на: § Моноалфавитные (щифр цезаря) - замены буква исходного текста заменяется на другую, заранее определенную букву. § Полиалфавитные(видженера) - для замены некоторого символа используются различные символы из некоторого набора. · Составные:DES, B-Crypt, Асимметричный шифр (открытым ключом)— система шифрования и/или ЭЦП, при которой открытый ключ передаётся по открытому каналу и используется для проверки ЭЦП и для шифрования сообщения. ЭЦП - информация в электронной форме, присоединенная к другой информации в электронной форме или иным образом связанная с такой информацией. Используется для определения лица, подписавшего информацию. Стеганография - это наука о скрытой передаче информации путём сохранения в тайне самого факта передачи. Преимущество стеганографии над чистой криптографией состоит в том, что сообщения не привлекают к себе внимания. Её разделяют на: Классическую и ЦВЗ. Классическая стеганография — запись на боковой стороне колоды карт, расположенных в условленном порядке; запись внутри варёного яйца; Компьютерная стеганография — направление стеганографии, основанное на особенностях компьютерной платформы; Цифровая стеганография — направление основанное на сокрытии или внедрении дополнительной информации в цифровые объекты, вызывая при этом некоторые искажения этих объектов (изображения, видео, аудио, текстуры 3D-объектов). ЦВЗ разделяются на: Стойкие – устойчивы ко всем видам атак. Робастые – устойчивы к определенному виду атак. Хрупкие - применяются как ЭЦП. Шифрування методом Цезаря. Зламування методу Цезаря При подстановке отдельные буквы открытого текста заменяются другими буквами или числами либо какими-то иными символами. Если открытый текст рассматривается как последовательность битов, то подстановка сводится к замене заданных последовательностей битов открытого текста заданными последовательностями битов зашифрованного текста. В шифре Цезаря каждая буква алфавита заменяется буквой, которая находится на три позиции дальше в этом же алфавите. Проще всего увидеть это на примере. Алфавит считается "циклическим", поэтому после Z идет А. Определить преобразование можно, перечислив все варианты, как показано ниже. Открытый текст: abcdefghijklmnopqrstuvwxyz Шифрованный текст: DEFGHIJKLMNOPQRSTUVWXYZABC Если каждой букве назначить числовой эквивалент (а=1, b=2 и т.д.), то алгоритм можно выразить следующими формулами. Каждая буква открытого текста р заменяется буквой шифрованного текста C = E(p) = (p + 3 )mod( 26 ). Алгоритм дешифрования: p = D(C) = (C - k)mod( 26 ). Если известно, что определенный текст был шифрован с помощью шифра Цезаря, то с помощью простого перебора всех вариантов раскрыть шифр очень просто — для этого достаточно проверить 25 возможных вариантов ключей. Криптостійкість шифрів Криптографическая стойкость — способность алгоритма противостоять всем возможным атакам против него. Стойким считается алгоритм, который для успешной атаки требует от противника недостижимых вычислительных ресурсов или недостижимого объема перехваченных открытых и зашифрованных сообщений или времени раскрытия, которое превышает время жизни интересующей противника информации. Практическая стойкость оценивается исключительно на какой-то определенный момент времени и c двух позиций: · вычислительная сложность прямого перебора (brute force) · известные на данный момент слабости (уязвимости) Начальная оценка Поскольку атака грубой силы возможна для большинства типов криптографического алгоритма, она может являться единственной существующей. Её оценка основываются на вычислительной сложности, которая может быть выражена во времени, деньгах, и ресурсах. Эта оценка пока является максимальной и минимальной одновременно. Текущая оценка Дальнейшее исследование алгоритма с целью поиска слабостей добавляет оценки стойкости по отношению к известным криптографическим атакам (Линейный криптоанализ, дифференциальный криптоанализ и более специфические) и могут понизить известную стойкость. Также важным способом проверки стойкости являются атаки на реализицию, выполняемые для конкретного программно-аппаратно-человеческого комплекса. Важность длительной проверки Чем более длительным и экспертным является анализ алгоритма и реализаций, тем более достоверной можно считать его стойкость. В нескольких случаях длительный и внимательный анализ приводил к снижению оценки стойкости ниже приемлемого уровня. Взлом Противник должен быть уверен в том, что шифрованный текст был получен либо с помощью моноалфавитной подстановки, либо с помощью шифра Виженера. Чтобы выяснить, какой именно из этих двух методов был использован: если использовалась моноалфавитная подстановка, статистические показатели шифрованного текста не будут отличаться от соответствующих показателей языка. Если такого статистического распределения нет, то все указывает на то, что был применен шифр Виженера. Вторым шагом надо определить длину ключевого слова. Решение этой задачи основано на следующей особенности: если начальные символы двух одинаковых последовательностей открытого текста находятся друг от друга на расстоянии, кратном длине ключа, эти последовательности будут представлены одинаковыми последовательностями и в шифрованном тексте. Аналитик, обнаружит повторяющуюся последовательность со смещением в несколько символов, и поэтому может предположить длину ключевого слова. Конечно, для повторившейся всего два раза последовательности совпадение может оказаться и случайным, а поэтому и не соответствовать шифрованным с одинаковыми ключевыми буквами одинаковым фрагментам открытого текста, но если сообщение будет достаточно длинным, то таких повторяющихся последовательностей в нем будет немало. Определив общий множитель для смещения начала таких последовательностей, аналитик узнает длину ключевого слова. Дальнейший анализ базируется на другой особенности данного шифра. Если ключевое слово имеет длину N, то шифр, состоит из N моноалфавитных подстановочных шифров. Это дает возможность использования известных характеристик частотных распределений букв открытого текста для взлома каждого моноалфавитного шифра по отдельности. Шифр тритениуса Алгоритм шифрования выглядит следующим образом: создается таблица замены, первой строкой которой является собственно сообщение, второй — алфавит, третьей — алфавит, сдвинутый на один шаг, и т. д. При шифровании первая буква сообщения заменяется буквой, стоящей под ней в первой строке, вторая буква — буквой, стоящей во второй строке, и т. д Шифр Гронсфельда Используется числовой ключ, а сама схема очень напоминает шифр Цезаря. Пусть нам надо зашифровать слово EXALTATION. Например, берём в качестве ключа число 31415, затем составляем следующую таблицу:
Получается, что каждой букве соответствует некая цифра, это цифра будет показывать, на сколько позиций будет происходить смещение алфавита для каждой конкретной буквы. Например, покажем, как преобразуется буква E:
То есть букве E соответствует буква H. Таким образом, для всего слова получаем зашифрованный текст: HYEMYDUMPS. Обратное преобразование происходит подобным образом, только каждый раз сдвигаем алфавит в другую сторону. Криптостойкость ключей Будь-яка криптосистема заснована на використанні ключової інформації, під якою розуміється вся сукупність діючих у АСОД ключів. За своїм призначенням останні діляться на ключі для шифрування ключів і ключі для шифрування даних. За часом життя діляться на довгострокові і короткочасні. Прикладом останніх є так звані сеансові ключі, що діють протягом тільки одного сеансу зв'язку. У поняття управління ключами входить сукупність методів вирішення таких завдань, як: • генерація ключів; • розподіл ключів; • зберігання ключів; • заміна ключів; • депонування ключів; • знищення ключів. Правильне рішення всіх перерахованих завдань має величезне значення, тому що в більшості випадків противнику набагато простіше провести атаку на ключову підсистему або на конкретну реалізацію криптоалгоритму, а не на сам цей алгоритм криптографічного захисту. Використання стійкого алгоритму шифрування є необхідним, але далеко не достатньою умовою побудови надійної системи криптографічного захисту інформації. Використовувані в процесі інформаційного обміну ключі потребують не менш надійного захисту на всіх стадіях свого життєвого циклу. К ключам симетричних та асиметричних криптосистем пред'являються різні вимоги. Цей факт слід враховувати при побудові гібридних криптосистем. В даний час надійними вважаються ключі розрядністю не менше 80 біт для систем з секретним ключем і не менше 1024 біт для систем з відкритим ключем, стійкість яких визначається складністю вирішення задачіфакторізаціі великих чисел (наприклад, RSA). У розпорядженні противника атакуючого криптосистему, завжди є дві можливості: випадкове вгадування ключа і повний перебір по всьому ключовому простору. Імовірність успіху в тому і в іншому випадку залежить від розрядності ключа. На практиці в гібридних криптосистемах довготривалий ключ для асиметричного алгоритму вибирають більш стійким, ніж сеансовий ключ для симетричного. Якщо супротивник володіє необмеженими фінансовими і технічними можливостями, для того щоб дізнатися ключ, йому необхідно лише витратити достатню кількість грошей. У разі противника з обмеженими можливостями при виборі розрядності ключа враховують такі міркування: • складність атаки повного перебору; • необхідну швидкодію криптоалгоритму в тих випадках, коли збільшення розміру ключа збільшує час роботи операцій шифрування; • час життя захищається інформації та її цінність; • можливості супротивника. Метод линейного сравнения
Последовательность случайных чисел {Х0} получается с помощью итераций следующего соотношения: Генератор BBS Сначала выбирается два больших простых числа,
Это просто означает, что
for
Проверка качества генераторов псевдослучайных чисел Предлагается три следующих критерия, по которым можно оценить качество любого генератора случайных чисел. T1. Генерирующая функция должна быть функцией полного периода, т.е. функция должна породить все числа от 0 до т прежде, чем числа начнут повторяться. Т2. Генерируемая последовательность должна вести себя как случайная. На самом деле эта последовательность не будет случайной, поскольку генерируется детерминированным алгоритмом, но существует множество статистических тестов, которые можно использовать для того, чтобы оценить степень случайности поведения последовательности. Т3. Генерирующая функция должна эффективно реализовываться в рамках 32-битовой арифметики. Стандарт шифрування DЕS (Data Encryption Standard — стандарт шифрования данных), принятом в 1977 году Национальным бюро стандартов (NBS) США, теперь называемым Национальным институтом стандартов и технологии (NIST). Этот стандарт — типичный представитель криптоалгоритмов, использующих симметричное шифрование. Сегодня стандарт шифрования DES используется в Соединенных Штатах, за небольшим исключением, практически везде. Правительственная связь, электронные банковские переводы, гражданские спутниковые коммуникации и даже пароли компьютерных систем — везде, в той или иной мере, применяется защита, основанная на DES. В соответствии с этим стандартом данные шифруются 64-битовыми блоками с использованием 56-битового ключа. Многошаговый алгоритм преобразует поступающие на вход 64-битовые блоки в 64-битовые блоки шифрованного текста. Тот же алгоритм с тем же ключом служит для обратного преобразования шифрованного текста в открытый. Одна из широко распространенных систем криптографической защиты, использующая стандарт DES, — разработанная в середине 80-х годов прошлого столетия система Kerberos, использование которой предполагает наличие высоконадежного сервера, хранящего исходные копии ключей для взаимодействия с каждым пользователем. Эта система представляет собой часть спецификации открытой вычислительной среды DCE (Distributed Computing Environment) фонда OSF. Среди предлагающих продукты на базе DCE такие компании, как IBM и HewlettPackard. Kerberos должна стать также частью системы защиты Windows NT 5.0. На практике криптографические системы с секретными ключами, как правило, быстрее систем с открытыми ключами, обеспечивающими ту же степень защиты. Однако преимущество последних в том, что они не позволяют отказаться от авторства, а также обеспечивают проверку целостности сообщений любого сорта. Стандарт шифрування RC5. RC5 — це алгоритм симетричного шифрування, розроблений Роном Райвестом в середині 90-х років. Характеристики Під час розробки RC5 ставилося завдання досягти наступних характеристик: Придатність для апаратної та програмної реалізації. В RC5 використовуються тільки елементарні обчислювальні операції, які зазвичай застосовуються в мікропроцесорах. Швидкість виконання. RC5 є простим алгоритмом, що працює з даними розміром в машинне слово. Усі основні операції передбачають також роботу з даними довжиною в слово. Адаптованість до процесорів з різною довжиною слова. Довжина слова в бітах є параметром RC5 — при зміні довжини слова змінюється сам алгоритм. Змінна кількість раундів. Кількість раундів є другим параметром RC5. Цей параметр дозволяє обрати оптимальне співвідношення між швидкістю роботи та ступенем захисту. Змінна довжина ключа. Довжина ключа є третім параметром RC5. Як і в попередньому випадку, цей параметр дозволяє знайти прийнятний компроміс між швидкістю роботи та необхідним рівнем безпеки. Простота. Структура RC5 дуже проста не тільки для реалізації, але й для оцінки її криптоаналітичної стійкості. Низькі вимоги до пам'яті. Низькі вимоги до пам'яті роблять RC5 придатним для використання в смарт-картах та інших подібних пристроях з обмеженим обсягом пам'яті. Високий ступінь захисту. RC5 покликаний забезпечити високий ступінь захисту за умови вибору відповідних значень параметрів. Залежність циклічних зсувів від даних. В RC5 використовуються циклічні зсуви, величина яких залежить від даних, що має підвищувати криптоаналітичну стійкість алгоритму. Параметри алгоритму RC5
Райвест пропонує використовувати RC5-32/12/16 в якості «стандартної» версії RC5. В алгоритмі RC5 виконуються три елементарні операції (а також обернені до них): Додавання. Додавання слів, позначене символом +, виконується по модулю 2w. Обернена операція, позначена символом -, є відніманням по модулю 2w. Побітове виключне АБО. Ця операція позначається символом Å. Циклічний зсув вліво. Циклічний зсув слова x вліво на y бітів позначається x<<<y. Обернена операція є циклічним зсувом слова x вправо на y бітів і позначається x>>>y. Шифрування Вхідні дані: відкритий текст M=(A,B) довжиною 2w бітів; кількість раундів r; ключ K=K[0]…K[b-1]. Вихідні дані: шифрований текст С довжиною 2w бітів. Обчислити (2r+2) підключів S[0]…S[2r+1] за відповідним алгоритмом з вхідного K та r. A:=A+S[0], B:=B+S[1] (додавання здійснюється за модулем 2w). For i=1 to r do: A:=((AÅB)<<<B)+S[2i], B:=((BÅA)<<<A)+S[2i+1]. Вихідним значенням є C:=(A,B). Дешифрування Для дешифрування використовуються ті самі підключі, які застосовуються для шифрованого тексту C=(A,B), таким чином (віднімання здійснюється за модулем 2w). For i=r downto 1 do: B:=((B-S[2i+1])>>>A)ÅA, A:=((A-S[2i])>>>B)ÅB. Результат M:=(A-S[0],B-S[1]). (рис. 1б) Створення підключів Підключі зберігаються в масиві з (2r+2) слів, елементи якого позначені S[0], S[1],…,S[2r+1]. Використовуючи в якості вхідних даних параметри r та w, цей масив ініціалізується псевдовипадковими фіксованими значеннями. Потім ключ K[0…b-1] довжиною b байтів перетворюється в масив L[0…c-1], що містить c слів. Для цього байти ключа копіюються в масив L доповнюючи при необхідності останнє слово справа нулями. Зрештою виконується деяка операція змішування, що об'єднує вміст L з ініціалізованими значеннями S, в результаті чого отримують остаточне значення масиву S. Стандарт шифрування IDEA. Початковий варіант алгоритму IDEA з'явився в 1990 р. Розробники алгоритму, Ксуеджа Лай (Xuejia Lai) і Джеймс Мессі (James Massey) зі Швейцарського інституту ETH Zurich, дали йому назву PES (Proposed Encryption Standard - пропонований стандарт шифрування), оскільки даний алгоритм був запропонований на заміну стандарту DES. Через рік алгоритм був модифікований з метою посилення криптостійкості до диференціального криптоаналізу. Нова версія одержала назву IPES (Improved PES - покращений PES), а ще через рік алгоритм змінив назву на IDEA (International Data Encryption Algorithm - міжнародний алгоритм шифрування даних). Основні характеристики і структура Алгоритм IDEA шифрує дані блоками по 64 біт, а ключ шифрування алгоритму має розмір 128 біт. Блок шифрованих даних розбивається на чотири 16-бітних субблока A, B, C і D (рис. 1), над якими виконується вісім раундів перетворень: A = A [x] Kr1 B = B + Kr2 C = C + Kr3 D = D [x] Kr4 T1 = A [+] C T2 = B [+] D T1 = T1 [x] Kr5 T2 = T1 + T2 T2 = T2 [x] Kr6 T1 = T1 + T2 A = A [+] T2 B = B [+] T1 C = C [+] T2 D = D [+] T1, де Krn - з'єднання n раунду r, "+" - операція додавання 16-бітових операндів за модулем 2 {в 16-й ступеня}, [+] - побітова логічна операція "виключає або" (XOR), [x] - множення 16 -бітових операндів за модулем (2 {в 16-й ступеня} + 1), причому в якості значення субблока, що складається з одних нулів, береться значення 2 {в 16-й ступеня}.
Після виконання описаних вище дій два внутрішніх субблока (B і C) міняються місцями - у всіх раундах, крім останнього. По завершенні восьми раундів виконуються додаткові перетворення (іноді звані дев'ятий раундом алгоритму): A '= A [x] K91 B '= B + K92 C '= C + K93 D '= D [x] K94 Шифртекст представляє собою результат конкатенації отриманих значень A ', B', C 'і D'. Операція розшифрування аналогічна зашифрування, з тією різницею, що при расшифровании використовуються модифіковані підключи і в іншій послідовності: K'r1 = (K (10-r) 1) -1 K'r2 =-K (10-r) 3 K'r3 =-K (10-r) 2 K'r4 = (K (10-r) 4) -1 K'r5 = K (9-r) 5 K'r6 = K (9-r) 6, за винятком раундів 1 і 9, в яких підключи K'r2 і K'r3 міняються місцями. Тут K'rn - з'єднання n раунду розшифрування r,-x і x-1 - зворотні значення x щодо описаних вище операцій додавання по модулю 2 {в 16-й ступеня} і множення за модулем (2 {в 16-й ступеня} + 1) відповідно. При цьому 0 {в-1-го ступеня} = 0. Процедура розширення ключа Завдання процедури розширення ключа - формування 52 16-бітових підключений, використовуваних у раундах шифрування і додаткових перетвореннях (тобто всього 832 біта ключової інформації). Ця процедура дуже проста, і виконується вона таким чином: 128-бітний ключ шифрування ділиться на вісім підключів по 16 біт; вони стають першими вісьмома підключами алгоритму (K11, K12, K13, K14, K15, K16, K21, K22). Ключ шифрування циклічно зсувається вліво на 25 біт. Результат ділиться на вісім наступних підключів. Ключ шифрування циклічно зсувається вліво на 25 біт, і так далі до вироблення необхідної кількості підключів. Крипостійкість алгоритму Вже в наступному році після появи алгоритму PES його автори опублікували роботу, в якій була доведена слабкість алгоритму по відношенню до диференціального криптоаналізу: для визначення ключа шифрування достатньо виконання 2 {в 64-го ступеня} операцій шифрування, тоді як повний перебір значень 128-бітного ключа зажадав б виконання 2 {в 128-го ступеня} операцій. Алгоритм IDEA з'явився в результаті досить незначних модифікацій алгоритму PES (рис. 2). Cлабкі ключі виключаються шляхом накладення операцією XOR спеціальної шістнадцятковій константи 0DAE на кожен з'єднання перед його використанням. Таким чином, незважаючи на виявлені недоліки, алгоритм IDEA вважається алгоритмом з високою криптостійкість. Незаперечна ж перевага даного алгоритму - висока швидкість зашифрування, не менше, ніж у два рази більше, ніж у алгоритму DES (залежно від платформи, на якій виконується шифрування). А можливість виконання операції розширення ключа "на льоту" (тобто паралельно з виконанням раундів шифрування) дуже вітається і в більш сучасних алгоритмах шифрування. Стандарт шифрування AES. Американський стандарт шифрування AES, покликаний замінити DES, вибирався на відкритому конкурсі, де всі зацікавлені організації і приватні особи могли вивчати і коментувати алгоритми-претенденти. Переможцем був оголошений алгоритм Rijndael, розроблений двома кріптографами з Бельгії. Алгоритм Rijndael представляє блок даних у вигляді двомірного байтового масиву розміром 4X4, 4X6 або 4X8 (допускається використання декількох фіксованих розмірів шифруєемого блоку інформації). Всі операції виконуються з окремими байтами масиву, а також з незалежними стовпцями і рядками. Алгоритм Rijndael виконує чотири перетворення: BS (ByteSub) - таблична заміна кожного байта масиву; SR (ShiftRow) - зсув рядків масиву. При цій операції перший рядок залишається без змін, а інші циклічно побайтно зсуються вліво на фіксоване число байт, що залежить від розміру масиву. Наприклад, для масиву розміром 4X4 рядки 2, 3 і 4 зсуються відповідно на 1, 2 і 3 байти. Далі йде MC (MixColumn) - операція над незалежними стовпцями масиву, коли кожен стовпець за певним правилом множиться на фіксовану матрицю c(x). І, нарешті, AK (AddRoundKey) - додавання ключа. Кожен біт масиву складається по модулю 2 з відповідним ключем раунду, що, у свою чергу, певним чином обчислюється із ключа шифрування. У кожному раунді (з деякими виключеннями) над даними, що шифруються, по черзі виконуються перераховані перетворення. Виключення стосуються першого і останнього раундів: перед першим раундом додатково виконується операція AK, а в останньому раунді відсутній MC. У результаті послідовність операцій при шифруванні виглядає так: AK, {BS, SR, MC, AK} (повторюється R-1 раз), BS, SR, AK. Кількість раундів шифрування (R) в алгоритмі Rijndael змінне (10, 12 або 14 раундів) і залежить від розмірів блоку і ключа шифрування (для ключа також передбачено кілька фіксованих розмірів). Розшифрування виконується за допомогою наступних зворотних операцій. Виконується обіг таблиці і таблична заміна на інверсній таблиці (щодо застосовуваної при шифруванні). Зворотна операція до SR - це циклічний зсув рядків вправо, а не вліво. Зворотна операція для MC - множення за тим же правилом на іншу матрицю d(x), що задовольняє умові: c(x) * d(x) = 1. Додавання ключа AK є зворотним самому собі, оскільки в ньому використається тільки операція XOR. Ці зворотні операції застосовуються при розшифруванні в послідовності, зворотної тієї, що використалася при шифруванні. Rijndael став новим стандартом шифрування даних завдяки цілому ряду переваг перед іншими алгоритмами. Насамперед він забезпечує високу швидкість шифрування на всіх платформах: як при програмній, так і при апаратній реалізації. Його відрізняють незрівнянно кращі можливості розпаралелювання обчислень у порівнянні з іншими алгоритмами, представленими на конкурс. Крім того, вимоги до ресурсів для його роботи мінімальні, що важливо при його використанні в пристроях, що володіють обмеженими обчислювальними можливостями. Недоліком же алгоритму можна вважати лише властиву йому нетрадиційну схему. Справа в тому, що властивості алгоритмів, заснованих на мережі Фейстеля, добре досліджені, а Rijndael, на відміну від них, може містити сховані уразливості, які можуть виявитися тільки через деякий час з моменту початку його широкого поширення. Лінійний криптоаналіз Іншим способом криптоаналізу є лінійний криптоаналіз, який використовує лінійні наближення перетворень, виконуваних алгоритмом шифрування. Даний метод дозволяє знайти ключ, маючи достатньо велике число пар (незашифрований текст, зашифрований текст). Розглянемо основні принципи, на яких базується лінійний криптоаналіз. Позначимо P [1],..., P [n] - незашифрований блок повідомлення. C [1],..., C [n] - зашифрований блок повідомлення. K [1],..., K [m] - ключ. A[i, j, …, k] = A[i]⊕A[j]⊕ …⊕A[k]. Метою лінійного криптоаналізу є пошук лінійного рівняння виду P[α1, α2, …, αa] ⊕C[β1, β2, …, βb ] = K[γ1, …, γc] Запускається з ймовірністю р ≠ 0.5. αi, βi і γi - фіксовані позиції в блоках повідомлення та ключі. Чим більше р. відхиляється від 0.5, тим більш відповідним вважається рівняння. Це рівняння означає, що якщо виконати операцію XOR над деякими бітами незашифрованого повідомлення і над деякими бітами зашифрованого повідомлення, вийде біт, що представляє собою XOR деяких бітів ключа. Це називається лінійним наближенням, яке може бути вірним з ймовірністю р. Рівняння складаються наступним чином. Обчислюються значення лівої частини для великого числа пар відповідних фрагментів незашифрованого і зашифрованого блоків. Якщо результат виявляється дорівнює нулю більш ніж у половині випадків, то вважають, що K [γ1,..., γс] = 0. Якщо в більшості випадків виходить 1, вважають, що K [γ1,..., γс] = 1. Таким чином отримують систему рівнянь, рішенням якої є ключ. Як і у випадку диференціального криптоаналізу, результати лінійного криптоаналізу повинні враховуватися при розробці алгоритмів симетричного шифрування. При розгляді методів криптоаналізу потокових шифрів всі методи можна умовно розділити на три класи: силові; статистичні; аналітичні атаки. До силовим атакам відносяться атаки, засновані на принципі повного перебору всіх можливих комбінацій ключа (атака «грубою силою»); при розробці схем шифрування розробники прагнуть до того, щоб при спробі розтину кріптосхеми даний вид атак був найбільш ефективним в порівнянні з іншими передбачуваними видами атак. До статистичним атакам відносяться атаки, засновані на оцінці статистичних властивостей гами шифрувальної (статистичний криптоаналіз). До аналітичних атакам відносять атаки, в яких алгоритм побудови атаки заснований на аналітичних принципах розтину криптосхеми. Силові атаки До цього класу належать атаки, здійснюють повний перебір всіх можливих варіантів. Складність повного перебору залежить від кількості всіх можливих рішень завдання (зокрема, розміру простору ключів або простору відкритих текстів). Цей клас атак застосуємо до всіх видів систем потокового шифрування. При розробці систем шифрування розробники прагнуть зробити так, щоб цей вид атак був найбільш ефективним в порівнянні з іншими існуючими методами злому. Статистичні атаки Статистичні атаки діляться на два підкласи: метод криптоаналізу статистичних властивостей шифрувальної гами: спрямований на вивчення вихідний послідовності криптосистеми; криптоаналітик намагається встановити значення наступного біта послідовності з імовірністю вище ймовірності випадкового вибору за допомогою різних статистичних тестів. метод криптоаналізу складності послідовності: криптоаналітик намагається знайти спосіб генерувати послідовність, аналогічну гамі, але більш просто реалізованим способом. Обидва методи використовують принцип лінійної складності. Аналітичні атаки Цей вид атак розглядається в припущенні, що криптоаналітик відомі опис генератора, відкритий і відповідний закритий тексти. Завдання криптоаналітик визначити використаний ключ (початкове заповнення регістрів). Види аналітичних атак, які застосовуються до синхронним потоковим шифрам: кореляційні компроміс "час-пам'ять" інверсійна "Припускай і визначай" на ключову завантаження і реініціалізацію XSL-атака Кореляційні атаки Є найбільш поширеними атаками для злому потокових шифрів. Відомо, що робота по розкриттю криптосистеми може бути значно скорочена, якщо нелінійна функція пропускає на вихід інформацію про внутрішні компонентах генератора. Тому для відновлення початкового заповнення регістрів кореляційні атаки досліджують кореляцію вихідний послідовності шіфросістеми з вихідною послідовністю регістрів. Існують наступні підкласи кореляційних атак: Базові кореляційні атаки Атаки, засновані на низько-вагових перевірках парності Атаки, засновані на використанні сверточних кодів Атаки, що використовують техніку турбо кодів Атаки, засновані на відновленні лінійних поліномів Швидкі кореляційні атаки. Компроміс «час-пам'ять» Мета даної атаки - відновлення початкового стану регістра зсуву (знаходження ключа), використовуючи відому схему пристрою та фрагмент шифрувальної послідовності. Складність атаки залежить від розміру шифру і довжини перехопленої гами. Складається з двох етапів: побудова великого словника, в якому записані всілякі пари «стан-вихід»; припущення про початковий заповненні регістра зсуву, генерація виходу, перегляд перехопленої вихідний послідовності і пошук відповідності зі сгенерованими виходом. Якщо сталася збіг, то дане можливе заповнення з великою ймовірністю є початковим. Прикладами цього класу атак є атака Стіва Беббідж і атака Бірюкова-Шаміра. «Припускай і визначай» Атака грунтується на припущенні, що криптоаналітик відомі гамма, поліном зворотного зв'язку, кількість зрушень регістра між виходами схеми і фільтруюча функція. Складається з трьох етапів: припущення про заповнення деяких осередків регістру; визначення повного заповнення регістра на підставі припущення про знання криптоаналітик; генерація вихідний послідовності; якщо вона збігається з гамою, то припущення на першому етапі було вірно, якщо не збігається, то повертаємося до етапу 1. Складність алгоритму залежить від пристрою генератора і від кількості припущень. Асиметрична криптографія. Асиметрична криптографія спочатку задумана як засіб передачі повідомлень від одного об'єкта до іншого (а не для конфіденційного збереження інформації, яку забезпечують тільки симетричні алгоритми). Тому подальше пояснення ми будемо вести в термінах "відправник" - особа, шифрує, а потім відправляє інформацію по незахищеному каналу і "одержувач" - особа, що приймає і відновлює інформацію в її початковому вигляді. Основна ідея асиметричних криптоалгоритмів полягає в тому, що для шифрування повідомлення використовується один ключ, а при дешифруванні - інший. Крім того, процедура шифрування обрана так, що вона необоротна навіть за відомим ключу шифрування - це друга необхідна умова асиметричної криптографії. Тобто, знаючи ключ шифрування і зашифрований текст, неможливо відновити вихідне повідомлення - прочитати його можна тільки за допомогою другого ключа - ключа дешифрування. А раз так, то ключ шифрування для відправки листів будь-якій особі можна взагалі не приховувати - знаючи його все одно неможливо прочитати зашифроване повідомлення. Тому, ключ шифрування називають в асиметричних системах "відкритим ключем", а ось ключ дешифрування одержувачу повідомлень необхідно тримати в секреті - він називається "закритим ключем". Напрошується питання: "Чому, знаючи відкритий ключ, не можна обчислити закритий ключ?" - Це третя необхідна умова асиметричної криптографії - алгоритми шифрування і дешифрування створюються так, щоб знаючи відкритий ключ, неможливо обчислити закритий ключ. У цілому система листування при використанні асиметричного шифрування виглядає наступним чином. Для кожного з N абонентів, що ведуть листування, обрана своя пара ключів: "відкритий" Ej і "закритий" Dj, де j - номер абонента. Всі відкриті ключі відомі всім користувачам мережі, кожен закритий ключ, навпаки, зберігається тільки у того абонента, якому він належить. Якщо абонент, скажімо під номером 7, збирається передати інформацію абоненту під номером 9, він шифрує дані ключем шифрування E9 і відправляє її абоненту 9. Незважаючи на те, що всі
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.93.14 (0.016 с.) |


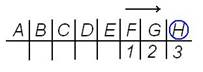
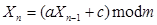 .
. и
и  , дающих при делении на 4 в остатке 3, т.е.
, дающих при делении на 4 в остатке 3, т.е. .
. . Например, для простых чисел 7 и 11 мы как раз имеем 7=11=3(mod 4). Пусть теперь
. Например, для простых чисел 7 и 11 мы как раз имеем 7=11=3(mod 4). Пусть теперь 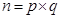 . Выберем случайное число
. Выберем случайное число  , взаимно простое с
, взаимно простое с  — в данном случае это означает, что ни
— в данном случае это означает, что ни 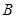 , в соответствии со следующим алгоритмом.
, в соответствии со следующим алгоритмом.
 to
to 





