
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полный и максимальный потоки в сети.Содержание книги
Поиск на нашем сайте
Поток наз. полным, если путь из источника в сток содержит хотя бы одну насыщенную дугу. Поток называется максимальным, если он принимает максимальное значение по сравнению с остальными потоками в сети. 29. Предика́т (n -местный, или n -арный) — это функция с множеством значений{0,1} (или «ложь» и «истина»), определённая на множестве § Квантор всеобщности (обозначение: § Квантор существования (обозначение: 34. (исчисление предикатов) — формальное исчисление, допускающее высказывания относительно переменных, фиксированных функций и предикатов. Расширяет логику высказываний. В свою очередь является частным случаем логики высшего порядка. 35. Доказательство теорем сводится к доказательству того, что некоторая формула 36. Под нечётким множеством
где § Пересечением нечётких множеств A и B называется наибольшее нечёткое подмножество, содержащееся одновременно в A и B:
§ Произведением нечётких множеств A и B называется нечёткое подмножество с функцией принадлежности:
§ Объединением нечётких множеств A и B называется наименьшее нечёткое подмножество, содержащее элементы A или B:
§ Суммой нечётких множеств A и B называется нечёткое подмножество с функцией принадлежности:
§ Отрицанием множества
для каждого
38. В терминах вычислимости по Тьюрингу, тезис гласит, что для любой интуитивно вычислимой функции существует вычисляющая её значениямашина Тьюринга. Иногда в такой формулировке фигурирует как тезис Тьюринга. В виду того, что классы частично вычислимых по Тьюрингу ичастично рекурсивных функций совпадают, утверждение объединяют в единый тезис Чёрча — Тьюринга. 40. Рекурси́вная фу́нкция (от лат. recursio — возвращение) — это числоваяфункция f (n) числового аргумента, которая в своей записи содержит себя же. Такая запись позволяет вычислять значения f (n) на основе значений
41. Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: qiaj→qi1aj1dk (если головка находится в состоянии qi, а в обозреваемой ячейке записана буква aj, то головка переходит в состояние qi1, в ячейку вместо aj записывается aj1, головка делает движение dk, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации <qi, aj> имеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины. 43. Различным формализациям представления об алгоритме отвечают различные формальные определения понятия перечислимого множества, оказывающиеся эквивалентными. Так, на основе понятия рекурсивной функции перечислимые множества натуральных чисел могут быть определены как образы частично рекурсивных функций одной переменной (поэтому перечислимые множества натуральных чисел иногда называют «рекурсивно перечислимыми множествами»). 45. Также известн В теории алгоритмов NP-полная задача — задача из класса NP, к которой можно свести любую другую задачу из класса NP за полиномиальное время. Таким образом, NP-полные задачи образуют в некотором смысле подмножество «самых сложных» задач в классе NP; и если для какой-то из них будет найден «быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро». о, что при условии 46. Однако, существуют алгоритмы поиска приближенных решений для метрической задачи за полиномиальное время и нахождения маршрута максимум вдвое длиннее оптимального. До сих пор не известен ни один алгоритм с полиномиальным временем, который бы гарантировал точность, лучшую чем 1,5 от оптимальной. По предположению 47. Вычислительные (численные) методы — методы решения математических задач в численном виде (см. Компьютерная алгебра)[1] Представление как исходных данных в задаче, так и её решения — в виде числа или набора чисел В системе подготовки инженеров технических специальностей является важной составляющей. 48. Покажем, как можно решить изначальную систему уравнений, не прибегая коптимизационным методам. В случае, если наша система представляет собойСЛАУ, целесообразно прибегнуть к таким методам, как метод Гаусса илиметод Ричардсона. Однако мы всё же будем исходить из предположения, что вид функции нам неизвестен и воспользуемся одним из итерационных методов численного решения. Среди большого разнообразия таковых выберем один из наиболее известных — метод Ньютона. Этот метод в свою очередь основывается на принципах метода простой итерации. Поэтому сначала будет изложена суть последнего. 51. раздел математики, изучающий вопрос о возможности приближенного представления одних математических объектов другими, как правило более простой природы, а также вопросы об оценках вносимой при этом погрешности. Значительная часть теории приближения относится к приближению одних функций другими, однако есть и результаты, относящиеся к абстрактным векторным или топологическим пространствам. 52. Интерполяция многочленами функции f(x) на отрезке [a, b] — построение многочлена Pn(x) степени меньшей или равной n, принимающего в узлах интерполяции x0, x1,..., xn значения f(xi):
Система уравнений, определяющих коэффициенты такого многочлена, имеет вид
Её определителем является определитель Вандермонда.
Он отличен от нуля при всяких попарно различных значениях xi, и интерполирование функции f по её значениям в узлах xi с помощью многочлена Pn(x) всегда возможно и единственно. 53. Численное дифференцирование — совокупность методов вычисления значения производной дискретно заданной функции. В основе численного дифференцирования лежит аппроксимация функции, от которой берется производная, интерполяционным многочленом. Все основные формулы численного дифференцирования могут быть получены при помощи первого интерполяционного многочлена Ньютона (формулы Ньютона для начала таблицы).Методы: 1) интерполяционного многочлена Ньютона. 54. Численное интегрирование (историческое название: (численная) квадратура) — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла. Численное интегрирование применяется, когда: 1. Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки. 2. Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например, f (x) = exp(− x 2).Методы:1)прямоугольников, 2)трапеций 3)парабол 4)увеличение точности 5)Гусса 6)Гаусса-Кронрода 7) Чебышева 8) интегрирование при бесконечных пределах 9)методы Монте-Карло 10) методы Рунге-Кутты 11) сплайнов. 55. Рассмотрим методы численного решения уравнений и систем уравнений:
или
Численное решение задачи можно проводить как непосредственно (используя одноимённые методы), так и с применением оптимизационных методов, приведя задачу к соответствующему виду. Последним посвящена статьяСистема уравнений и экстремальные задачи. Градиентные методы.
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 918; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 . Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный». Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката. Чаще всего упоминают:
. Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный». Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката. Чаще всего упоминают: , читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…»).
, читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…»). , читается: «существует…» или «найдётся…»).
, читается: «существует…» или «найдётся…»). (гипотеза теоремы) является логическим следствием множества формул
(гипотеза теоремы) является логическим следствием множества формул 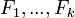 (допущений). Т.е. сама теорема может быть сформулирована следующим образом: "если
(допущений). Т.е. сама теорема может быть сформулирована следующим образом: "если  понимается совокупность
понимается совокупность ,
, — универсальное множество, а
— универсальное множество, а 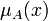 — функция принадлежности (характеристическая функция), характеризующая степень принадлежности элемента
— функция принадлежности (характеристическая функция), характеризующая степень принадлежности элемента 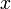 нечёткому множеству
нечёткому множеству 
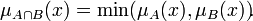



 с функцией принадлежности:
с функцией принадлежности: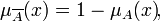
 .
. , подобно рассуждению по индукции. Чтобы вычисление завершалось для любого n, необходимо, чтобы для некоторых n функция была определена нерекурсивно (например, для n = 0,1). Вот пример рекурсивной функции, дающей n -ое число Фибоначчи:
, подобно рассуждению по индукции. Чтобы вычисление завершалось для любого n, необходимо, чтобы для некоторых n функция была определена нерекурсивно (например, для n = 0,1). Вот пример рекурсивной функции, дающей n -ое число Фибоначчи:
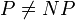 не существует алгоритма, который для некоторого полинома p вычислял бы такие решения задачи коммивояжера, которые отличались бы от оптимального максимум на коэффициент 2 p (n).
не существует алгоритма, который для некоторого полинома p вычислял бы такие решения задачи коммивояжера, которые отличались бы от оптимального максимум на коэффициент 2 p (n).







